Tensor

class paddle. Tensor ( self, /, value, place, persistable, zero_copy, name, stop_gradient, dims, dtype, type ) [source]

Tensor is the basic data structure in PaddlePaddle. There are some ways to create a Tensor:

Use the existing data to create a Tensor, please refer to to_tensor.
Create a Tensor with a specified shape, please refer to ones, zeros, full.
Create a Tensor with the same shape and dtype as other Tensor, please refer to ones_like, zeros_like, full_like.

abs ( name: str | None = None ) → Tensor [source] abs¶

Perform elementwise abs for input x.

\[out = |x|\]

Parameters

x (Tensor) – The input Tensor with data type int32, int64, float16, float32, float64, complex64 and complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor.A Tensor with the same data type and shape as $x$.

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.abs(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.40000001, 0.20000000, 0.10000000, 0.30000001])

abs_ ( name=None ) abs_¶: Inplace version of abs API, the output Tensor will be inplaced with input x. Please refer to abs.

acos ( name: str | None = None ) → Tensor [source] acos¶

Acos Activation Operator.

\[out = cos^{-1}(x)\]

Parameters

x (Tensor) – Input of Acos operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Acos operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.acos(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.98231316, 1.77215421, 1.47062886, 1.26610363])

acos_ ( name=None ) acos_¶: Inplace version of acos API, the output Tensor will be inplaced with input x. Please refer to acos.

acosh ( name: str | None = None ) → Tensor [source] acosh¶

Acosh Activation Operator.

\[out = acosh(x)\]

Parameters

x (Tensor) – Input of Acosh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Acosh operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([1., 3., 4., 5.])
>>> out = paddle.acosh(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.        , 1.76274717, 2.06343699, 2.29243159])

acosh_ ( name=None ) acosh_¶: Inplace version of acosh API, the output Tensor will be inplaced with input x. Please refer to acosh.

add ( y: Tensor, name: str | None = None ) → Tensor [source] add¶

Elementwise Add Operator. Add two tensors element-wise The equation is:

\[Out=X+Y\]

$X$ the tensor of any dimension. $Y$ the tensor whose dimensions must be less than or equal to the dimensions of $X$.

This operator is used in the following cases:

The shape of $Y$ is the same with $X$.

The shape of $Y$ is a continuous subsequence of $X$.

For example:

shape(X) = (2, 3, 4, 5), shape(Y) = (,)
shape(X) = (2, 3, 4, 5), shape(Y) = (5,)
shape(X) = (2, 3, 4, 5), shape(Y) = (4, 5), with axis=-1(default) or axis=2
shape(X) = (2, 3, 4, 5), shape(Y) = (3, 4), with axis=1
shape(X) = (2, 3, 4, 5), shape(Y) = (2), with axis=0
shape(X) = (2, 3, 4, 5), shape(Y) = (2, 1), with axis=0

Parameters

x (Tensor) – Tensor of any dimensions. Its dtype should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
y (Tensor) – Tensor of any dimensions. Its dtype should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

N-D Tensor. A location into which the result is stored. It’s dimension equals with x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 4], 'float64')
>>> y = paddle.to_tensor([1, 5, 2], 'float64')
>>> z = paddle.add(x, y)
>>> print(z)
Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True,
[3., 8., 6.])

add_ ( y: Tensor, name: str | None = None ) → Tensor add_¶: Inplace version of add API, the output Tensor will be inplaced with input x. Please refer to add.

add_n ( name: str | None = None ) → Tensor [source] add_n¶

Sum one or more Tensor of the input.

For example:

Case 1:

    Input:
        input.shape = [2, 3]
        input = [[1, 2, 3],
                 [4, 5, 6]]

    Output:
        output.shape = [2, 3]
        output = [[1, 2, 3],
                  [4, 5, 6]]

Case 2:

    Input:
        First input:
            input1.shape = [2, 3]
            Input1 = [[1, 2, 3],
                      [4, 5, 6]]

        The second input:
            input2.shape = [2, 3]
            input2 = [[7, 8, 9],
                      [10, 11, 12]]

        Output:
            output.shape = [2, 3]
            output = [[8, 10, 12],
                      [14, 16, 18]]

Parameters

inputs (Tensor|list[Tensor]|tuple[Tensor]) – A Tensor or a list/tuple of Tensors. The shape and data type of the list/tuple elements should be consistent. Input can be multi-dimensional Tensor, and data types can be: bfloat16, float16, float32, float64, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the sum of input $inputs$ , its shape and data types are consistent with $inputs$.

Examples

>>> import paddle

>>> input0 = paddle.to_tensor([[1, 2, 3], [4, 5, 6]], dtype='float32')
>>> input1 = paddle.to_tensor([[7, 8, 9], [10, 11, 12]], dtype='float32')
>>> output = paddle.add_n([input0, input1])
>>> output
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[8. , 10., 12.],
 [14., 16., 18.]])

addmm ( x: Tensor, y: Tensor, beta: float = 1.0, alpha: float = 1.0, name: str | None = None ) → Tensor [source] addmm¶

addmm

Perform matrix multiplication for input $x$ and $y$. $input$ is added to the final result. The equation is:

\[Out = alpha * x * y + beta * input\]

$Input$, $x$ and $y$ can carry the LoD (Level of Details) information, or not. But the output only shares the LoD information with input $input$.

Parameters

input (Tensor) – The input Tensor to be added to the final result.
x (Tensor) – The first input Tensor for matrix multiplication.
y (Tensor) – The second input Tensor for matrix multiplication.
beta (float, optional) – Coefficient of $input$, default is 1.
alpha (float, optional) – Coefficient of $x*y$, default is 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output Tensor of addmm.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.ones([2, 2])
>>> y = paddle.ones([2, 2])
>>> input = paddle.ones([2, 2])

>>> out = paddle.addmm(input=input, x=x, y=y, beta=0.5, alpha=5.0)

>>> print(out)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[10.50000000, 10.50000000],
 [10.50000000, 10.50000000]])

addmm_ ( x: Tensor, y: Tensor, beta: float = 1.0, alpha: float = 1.0, name: str | None = None ) → Tensor [source] addmm_¶: Inplace version of addmm API, the output Tensor will be inplaced with input input. Please refer to addmm.

all ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] all¶

Computes the logical and of tensor elements over the given dimension.

Parameters

x (Tensor) – An N-D Tensor, the input data type should be ‘bool’, ‘float32’, ‘float64’, ‘int32’, ‘int64’, ‘complex64’, ‘complex128’.
axis (int|list|tuple|None, optional) – The dimensions along which the logical and is compute. If None, and all elements of x and return a Tensor with a single element, otherwise must be in the range $[-rank(x), rank(x))$. If $axis[i] < 0$, the dimension to reduce is $rank + axis[i]$.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Results the logical and on the specified axis of input Tensor x, it’s data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> # x is a bool Tensor with following elements:
>>> #    [[True, False]
>>> #     [True, True]]
>>> x = paddle.to_tensor([[1, 0], [1, 1]], dtype='int32')
>>> x
Tensor(shape=[2, 2], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 0],
 [1, 1]])
>>> x = paddle.cast(x, 'bool')

>>> # out1 should be False
>>> out1 = paddle.all(x)
>>> out1
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
False)

>>> # out2 should be [True, False]
>>> out2 = paddle.all(x, axis=0)
>>> out2
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False])

>>> # keepdim=False, out3 should be [False, True], out.shape should be (2,)
>>> out3 = paddle.all(x, axis=-1)
>>> out3
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True ])

>>> # keepdim=True, out4 should be [[False], [True]], out.shape should be (2, 1)
>>> out4 = paddle.all(x, axis=1, keepdim=True)
>>> out4
Tensor(shape=[2, 1], dtype=bool, place=Place(cpu), stop_gradient=True,
[[False],
 [True ]])

allclose ( y: Tensor, rtol: float = 1e-05, atol: float = 1e-08, equal_nan: bool = False, name: str | None = None ) → Tensor [source] allclose¶

Check if all $x$ and $y$ satisfy the condition:

\[\left| x - y \right| \leq atol + rtol \times \left| y \right|\]

elementwise, for all elements of $x$ and $y$. This is analogous to $numpy.allclose$, namely that it returns $True$ if two tensors are elementwise equal within a tolerance.

Parameters

x (Tensor) – The input tensor, it’s data type should be float16, float32, float64.
y (Tensor) – The input tensor, it’s data type should be float16, float32, float64.
rtol (float, optional) – The relative tolerance. Default: $1e-5$ .
atol (float, optional) – The absolute tolerance. Default: $1e-8$ .
equal_nan (bool, optional) – ${equal_nan_comment}. Default: False.
name (str|None, optional) – Name for the operation. For more information, please refer to Name. Default: None.

Returns

The output tensor, it’s data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([10000., 1e-07])
>>> y = paddle.to_tensor([10000.1, 1e-08])
>>> result1 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=False, name="ignore_nan")
>>> print(result1)
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
False)
>>> result2 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=True, name="equal_nan")
>>> print(result2)
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
False)
>>> x = paddle.to_tensor([1.0, float('nan')])
>>> y = paddle.to_tensor([1.0, float('nan')])
>>> result1 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=False, name="ignore_nan")
>>> print(result1)
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
False)
>>> result2 = paddle.allclose(x, y, rtol=1e-05, atol=1e-08, equal_nan=True, name="equal_nan")
>>> print(result2)
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
True)

amax ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] amax¶

Computes the maximum of tensor elements over the given axis.

Note

The difference between max and amax is: If there are multiple maximum elements, amax evenly distributes gradient between these equal values, while max propagates gradient to all of them.

Parameters

x (Tensor) – A tensor, the data type is float32, float64, int32, int64, the dimension is no more than 4.
axis (int|list|tuple|None, optional) – The axis along which the maximum is computed. If None, compute the maximum over all elements of x and return a Tensor with a single element, otherwise must be in the range $[-x.ndim(x), x.ndim(x))$. If $axis[i] < 0$, the axis to reduce is $x.ndim + axis[i]$.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of maximum on the specified axis of input tensor, it’s data type is the same as x.

Examples

>>> import paddle
>>> # data_x is a Tensor with shape [2, 4] with multiple maximum elements
>>> # the axis is a int element

>>> x = paddle.to_tensor([[0.1, 0.9, 0.9, 0.9],
...                         [0.9, 0.9, 0.6, 0.7]],
...                         dtype='float64', stop_gradient=False)
>>> # There are 5 maximum elements:
>>> # 1) amax evenly distributes gradient between these equal values,
>>> #    thus the corresponding gradients are 1/5=0.2;
>>> # 2) while max propagates gradient to all of them,
>>> #    thus the corresponding gradient are 1.
>>> result1 = paddle.amax(x)
>>> result1.backward()
>>> result1
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False,
0.90000000)
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.20000000, 0.20000000, 0.20000000],
 [0.20000000, 0.20000000, 0.        , 0.        ]])

>>> x.clear_grad()
>>> result1_max = paddle.max(x)
>>> result1_max.backward()
>>> result1_max
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False,
0.90000000)
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0., 1., 1., 1.],
 [1., 1., 0., 0.]])

>>> x.clear_grad()
>>> result2 = paddle.amax(x, axis=0)
>>> result2.backward()
>>> result2
Tensor(shape=[4], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.90000000, 0.90000000, 0.90000000, 0.90000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.50000000, 1.        , 1.        ],
 [1.        , 0.50000000, 0.        , 0.        ]])

>>> x.clear_grad()
>>> result3 = paddle.amax(x, axis=-1)
>>> result3.backward()
>>> result3
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.90000000, 0.90000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.33333333, 0.33333333, 0.33333333],
 [0.50000000, 0.50000000, 0.        , 0.        ]])

>>> x.clear_grad()
>>> result4 = paddle.amax(x, axis=1, keepdim=True)
>>> result4.backward()
>>> result4
Tensor(shape=[2, 1], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.90000000],
 [0.90000000]])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.33333333, 0.33333333, 0.33333333],
 [0.50000000, 0.50000000, 0.        , 0.        ]])

>>> # data_y is a Tensor with shape [2, 2, 2]
>>> # the axis is list
>>> y = paddle.to_tensor([[[0.1, 0.9], [0.9, 0.9]],
...                         [[0.9, 0.9], [0.6, 0.7]]],
...                         dtype='float64', stop_gradient=False)
>>> result5 = paddle.amax(y, axis=[1, 2])
>>> result5.backward()
>>> result5
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.90000000, 0.90000000])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[0.        , 0.33333333],
  [0.33333333, 0.33333333]],
 [[0.50000000, 0.50000000],
  [0.        , 0.        ]]])

>>> y.clear_grad()
>>> result6 = paddle.amax(y, axis=[0, 1])
>>> result6.backward()
>>> result6
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.90000000, 0.90000000])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[0.        , 0.33333333],
  [0.50000000, 0.33333333]],
 [[0.50000000, 0.33333333],
  [0.        , 0.        ]]])

amin ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] amin¶

Computes the minimum of tensor elements over the given axis

Note

The difference between min and amin is: If there are multiple minimum elements, amin evenly distributes gradient between these equal values, while min propagates gradient to all of them.

Parameters

x (Tensor) – A tensor, the data type is float32, float64, int32, int64, the dimension is no more than 4.
axis (int|list|tuple|None, optional) – The axis along which the minimum is computed. If None, compute the minimum over all elements of x and return a Tensor with a single element, otherwise must be in the range $[-x.ndim, x.ndim)$. If $axis[i] < 0$, the axis to reduce is $x.ndim + axis[i]$.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of minimum on the specified axis of input tensor, it’s data type is the same as input’s Tensor.

Examples

>>> import paddle
>>> # data_x is a Tensor with shape [2, 4] with multiple minimum elements
>>> # the axis is a int element

>>> x = paddle.to_tensor([[0.2, 0.1, 0.1, 0.1],
...                         [0.1, 0.1, 0.6, 0.7]],
...                         dtype='float64', stop_gradient=False)
>>> # There are 5 minimum elements:
>>> # 1) amin evenly distributes gradient between these equal values,
>>> #    thus the corresponding gradients are 1/5=0.2;
>>> # 2) while min propagates gradient to all of them,
>>> #    thus the corresponding gradient are 1.
>>> result1 = paddle.amin(x)
>>> result1.backward()
>>> result1
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False,
0.10000000)
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.20000000, 0.20000000, 0.20000000],
 [0.20000000, 0.20000000, 0.        , 0.        ]])

>>> x.clear_grad()
>>> result1_min = paddle.min(x)
>>> result1_min.backward()
>>> result1_min
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False,
0.10000000)
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0., 1., 1., 1.],
 [1., 1., 0., 0.]])

>>> x.clear_grad()
>>> result2 = paddle.amin(x, axis=0)
>>> result2.backward()
>>> result2
Tensor(shape=[4], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.10000000, 0.10000000, 0.10000000, 0.10000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.50000000, 1.        , 1.        ],
 [1.        , 0.50000000, 0.        , 0.        ]])

>>> x.clear_grad()
>>> result3 = paddle.amin(x, axis=-1)
>>> result3.backward()
>>> result3
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.10000000, 0.10000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.33333333, 0.33333333, 0.33333333],
 [0.50000000, 0.50000000, 0.        , 0.        ]])

>>> x.clear_grad()
>>> result4 = paddle.amin(x, axis=1, keepdim=True)
>>> result4.backward()
>>> result4
Tensor(shape=[2, 1], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.10000000],
 [0.10000000]])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.        , 0.33333333, 0.33333333, 0.33333333],
 [0.50000000, 0.50000000, 0.        , 0.        ]])

>>> # data_y is a Tensor with shape [2, 2, 2]
>>> # the axis is list
>>> y = paddle.to_tensor([[[0.2, 0.1], [0.1, 0.1]],
...                       [[0.1, 0.1], [0.6, 0.7]]],
...                       dtype='float64', stop_gradient=False)
>>> result5 = paddle.amin(y, axis=[1, 2])
>>> result5.backward()
>>> result5
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.10000000, 0.10000000])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[0.        , 0.33333333],
  [0.33333333, 0.33333333]],
 [[0.50000000, 0.50000000],
  [0.        , 0.        ]]])

>>> y.clear_grad()
>>> result6 = paddle.amin(y, axis=[0, 1])
>>> result6.backward()
>>> result6
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.10000000, 0.10000000])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[0.        , 0.33333333],
  [0.50000000, 0.33333333]],
 [[0.50000000, 0.33333333],
  [0.        , 0.        ]]])

angle ( name: str | None = None ) → Tensor [source] angle¶

Element-wise angle of complex numbers. For non-negative real numbers, the angle is 0 while for negative real numbers, the angle is $\pi$, and NaNs are propagated..

Equation:: \[angle(x)=arctan2(x.imag, x.real)\]

Parameters

x (Tensor) – An N-D Tensor, the data type is complex64, complex128, or float32, float64 .
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor of real data type with the same precision as that of x’s data type.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([-2, -1, 0, 1]).unsqueeze(-1).astype('float32')
>>> y = paddle.to_tensor([-2, -1, 0, 1]).astype('float32')
>>> z = x + 1j * y
>>> z
Tensor(shape=[4, 4], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[(-2-2j), (-2-1j), (-2+0j), (-2+1j)],
 [(-1-2j), (-1-1j), (-1+0j), (-1+1j)],
 [-2j    , -1j    ,  0j    ,  1j    ],
 [ (1-2j),  (1-1j),  (1+0j),  (1+1j)]])

>>> theta = paddle.angle(z)
>>> theta
Tensor(shape=[4, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[-2.35619450, -2.67794514,  3.14159274,  2.67794514],
 [-2.03444386, -2.35619450,  3.14159274,  2.35619450],
 [-1.57079637, -1.57079637,  0.        ,  1.57079637],
 [-1.10714877, -0.78539819,  0.        ,  0.78539819]])

any ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] any¶

Computes the logical or of tensor elements over the given dimension, and return the result.

Parameters

x (Tensor) – An N-D Tensor, the input data type should be ‘bool’, ‘float32’, ‘float64’, ‘int32’, ‘int64’, ‘complex64’, ‘complex128’.
axis (int|list|tuple|None, optional) – The dimensions along which the logical or is compute. If None, and all elements of x and return a Tensor with a single element, otherwise must be in the range $[-rank(x), rank(x))$. If $axis[i] < 0$, the dimension to reduce is $rank + axis[i]$.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Results the logical or on the specified axis of input Tensor x, it’s data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 0], [1, 1]], dtype='int32')
>>> x = paddle.assign(x)
>>> x
Tensor(shape=[2, 2], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 0],
 [1, 1]])
>>> x = paddle.cast(x, 'bool')
>>> # x is a bool Tensor with following elements:
>>> #    [[True, False]
>>> #     [True, True]]

>>> # out1 should be True
>>> out1 = paddle.any(x)
>>> out1
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
True)

>>> # out2 should be [True, True]
>>> out2 = paddle.any(x, axis=0)
>>> out2
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[True, True])

>>> # keepdim=False, out3 should be [True, True], out.shape should be (2,)
>>> out3 = paddle.any(x, axis=-1)
>>> out3
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[True, True])

>>> # keepdim=True, result should be [[True], [True]], out.shape should be (2,1)
>>> out4 = paddle.any(x, axis=1, keepdim=True)
>>> out4
Tensor(shape=[2, 1], dtype=bool, place=Place(cpu), stop_gradient=True,
[[True],
 [True]])

apply ( func: Callable[[Tensor], Tensor] ) → Tensor apply¶

Apply the python function to the tensor.

Returns: None

Examples

>>> import paddle

>>> x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("cpu", "float64")
>>> f = lambda x: 3*x+2
>>> y = x.apply(f)
>>> print(y)
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
       [[2.90000004, 3.50000000, 2.30000000],
        [4.69999993, 4.69999993, 4.09999996],
        [3.20000002, 4.40000004, 2.60000001]])


>>> x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("cpu", "float16")
>>> y = x.apply(f)


>>> x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("cpu", "bfloat16")
>>> y = x.apply(f)


>>> if paddle.is_compiled_with_cuda():
>>>     x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("gpu", "float32")
>>>     y = x.apply(f)

apply_ ( func: Callable[[Tensor], Tensor] ) → Tensor apply_¶

Inplace apply the python function to the tensor.

Returns: None

Examples

>>> import paddle

>>> x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("cpu", "float64")
>>> f = lambda x: 3*x+2
>>> x.apply_(f)
>>> print(x)
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
       [[2.90000004, 3.50000000, 2.30000000],
        [4.69999993, 4.69999993, 4.09999996],
        [3.20000002, 4.40000004, 2.60000001]])


>>> x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("cpu", "float16")
>>> x.apply_(f)


>>> x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("cpu", "bfloat16")
>>> x.apply_(f)


>>> if paddle.is_compiled_with_cuda():
>>>     x = paddle.to_tensor([[0.3, 0.5, 0.1],
>>>        [0.9, 0.9, 0.7],
>>>        [0.4, 0.8, 0.2]]).to("gpu", "float32")
>>>     x.apply_(f)

argmax ( axis: int | None = None, keepdim: bool = False, dtype: DTypeLike = 'int64', name: str | None = None ) → Tensor [source] argmax¶

Computes the indices of the max elements of the input tensor’s element along the provided axis.

Parameters

x (Tensor) – An input N-D Tensor with type float16, float32, float64, int16, int32, int64, uint8.
axis (int|None, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is None, the input x will be into the flatten tensor, and selecting the min value index.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
dtype (str|np.dtype, optional) – Data type of the output tensor which can be int32, int64. The default value is int64 , and it will return the int64 indices.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, return the tensor of int32 if set dtype is int32, otherwise return the tensor of int64.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[5,8,9,5],
...                       [0,0,1,7],
...                       [6,9,2,4]])
>>> out1 = paddle.argmax(x)
>>> print(out1.numpy())
2
>>> out2 = paddle.argmax(x, axis=0)
>>> print(out2.numpy())
[2 2 0 1]
>>> out3 = paddle.argmax(x, axis=-1)
>>> print(out3.numpy())
[2 3 1]
>>> out4 = paddle.argmax(x, axis=0, keepdim=True)
>>> print(out4.numpy())
[[2 2 0 1]]

argmin ( axis: int | None = None, keepdim: bool = False, dtype: DTypeLike = 'int64', name: str | None = None ) → Tensor [source] argmin¶

Computes the indices of the min elements of the input tensor’s element along the provided axis.

Parameters

x (Tensor) – An input N-D Tensor with type float16, float32, float64, int16, int32, int64, uint8.
axis (int|None, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is None, the input x will be into the flatten tensor, and selecting the min value index.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
dtype (str|np.dtype, optional) – Data type of the output tensor which can be int32, int64. The default value is ‘int64’, and it will return the int64 indices.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, return the tensor of int32 if set dtype is int32, otherwise return the tensor of int64.

Examples

>>> import paddle

>>> x =  paddle.to_tensor([[5,8,9,5],
...                        [0,0,1,7],
...                        [6,9,2,4]])
>>> out1 = paddle.argmin(x)
>>> print(out1.numpy())
4
>>> out2 = paddle.argmin(x, axis=0)
>>> print(out2.numpy())
[1 1 1 2]
>>> out3 = paddle.argmin(x, axis=-1)
>>> print(out3.numpy())
[0 0 2]
>>> out4 = paddle.argmin(x, axis=0, keepdim=True)
>>> print(out4.numpy())
[[1 1 1 2]]

argsort ( axis: int = -1, descending: bool = False, stable: bool = False, name: str | None = None ) → Tensor [source] argsort¶

Sorts the input along the given axis, and returns the corresponding index tensor for the sorted output values. The default sort algorithm is ascending, if you want the sort algorithm to be descending, you must set the descending as True.

Parameters

x (Tensor) – An input N-D Tensor with type bfloat16, float16, float32, float64, int16, int32, int64, uint8.
axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is Rank(x). when axis<0, it works the same way as axis+R. Default is -1.
descending (bool, optional) – Descending is a flag, if set to true, algorithm will sort by descending order, else sort by ascending order. Default is false.
stable (bool, optional) – Whether to use stable sorting algorithm or not. When using stable sorting algorithm, the order of equivalent elements will be preserved. Default is False.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, sorted indices(with the same shape as x and with data type int64).

Examples

>>> import paddle

>>> x = paddle.to_tensor([[[5,8,9,5],
...                        [0,0,1,7],
...                        [6,9,2,4]],
...                       [[5,2,4,2],
...                        [4,7,7,9],
...                        [1,7,0,6]]],
...                      dtype='float32')
>>> out1 = paddle.argsort(x, axis=-1)
>>> out2 = paddle.argsort(x, axis=0)
>>> out3 = paddle.argsort(x, axis=1)

>>> print(out1)
Tensor(shape=[2, 3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[0, 3, 1, 2],
  [0, 1, 2, 3],
  [2, 3, 0, 1]],
 [[1, 3, 2, 0],
  [0, 1, 2, 3],
  [2, 0, 3, 1]]])

>>> print(out2)
Tensor(shape=[2, 3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[0, 1, 1, 1],
  [0, 0, 0, 0],
  [1, 1, 1, 0]],
 [[1, 0, 0, 0],
  [1, 1, 1, 1],
  [0, 0, 0, 1]]])

>>> print(out3)
Tensor(shape=[2, 3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[1, 1, 1, 2],
  [0, 0, 2, 0],
  [2, 2, 0, 1]],
 [[2, 0, 2, 0],
  [1, 1, 0, 2],
  [0, 2, 1, 1]]])

>>> x = paddle.to_tensor([1, 0]*40, dtype='float32')
>>> out1 = paddle.argsort(x, stable=False)
>>> out2 = paddle.argsort(x, stable=True)

>>> print(out1)
Tensor(shape=[80], dtype=int64, place=Place(cpu), stop_gradient=True,
[55, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 1 , 57, 59, 61,
 63, 65, 67, 69, 71, 73, 75, 77, 79, 17, 11, 13, 25, 7 , 3 , 27, 23, 19,
 15, 5 , 21, 9 , 10, 64, 62, 68, 60, 58, 8 , 66, 14, 6 , 70, 72, 4 , 74,
 76, 2 , 78, 0 , 20, 28, 26, 30, 32, 24, 34, 36, 22, 38, 40, 12, 42, 44,
 18, 46, 48, 16, 50, 52, 54, 56])

>>> print(out2)
Tensor(shape=[80], dtype=int64, place=Place(cpu), stop_gradient=True,
[1 , 3 , 5 , 7 , 9 , 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35,
 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71,
 73, 75, 77, 79, 0 , 2 , 4 , 6 , 8 , 10, 12, 14, 16, 18, 20, 22, 24, 26,
 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62,
 64, 66, 68, 70, 72, 74, 76, 78])

as_complex ( name: str | None = None ) → Tensor [source] as_complex¶

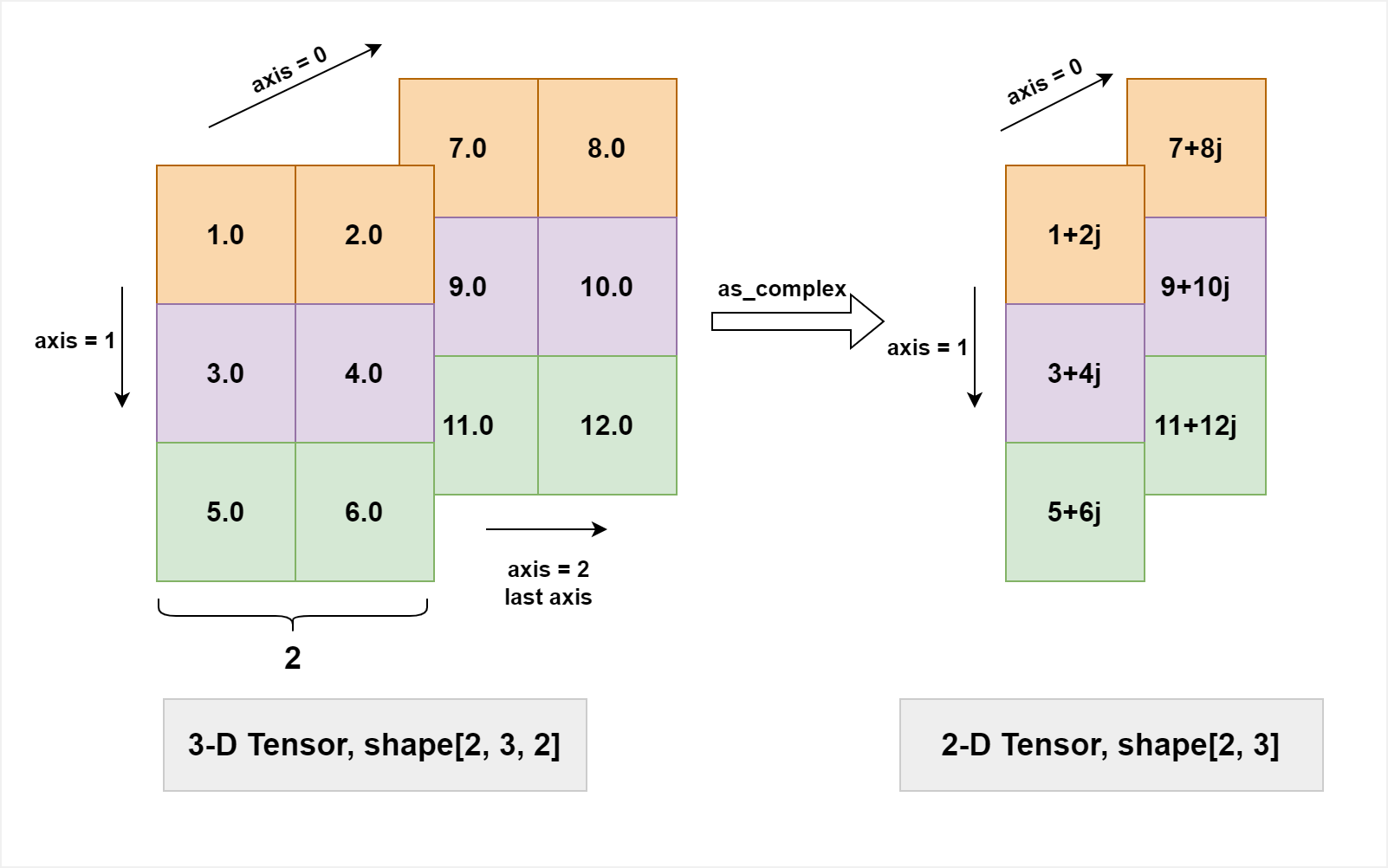
Transform a real tensor to a complex tensor.

The data type of the input tensor is ‘float32’ or ‘float64’, and the data type of the returned tensor is ‘complex64’ or ‘complex128’, respectively.

The shape of the input tensor is (* ,2), (* means arbitrary shape), i.e. the size of the last axis should be 2, which represent the real and imag part of a complex number. The shape of the returned tensor is (*,).

The image below demonstrates the case that a real 3D-tensor with shape [2, 3, 2] is transformed into a complex 2D-tensor with shape [2, 3].

Parameters

x (Tensor) – The input tensor. Data type is ‘float32’ or ‘float64’.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, The output. Data type is ‘complex64’ or ‘complex128’, with the same precision as the input.

Examples

>>> import paddle
>>> x = paddle.arange(12, dtype=paddle.float32).reshape([2, 3, 2])
>>> y = paddle.as_complex(x)
>>> print(y)
Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[1j      , (2+3j)  , (4+5j)  ],
 [(6+7j)  , (8+9j)  , (10+11j)]])

as_real ( name: str | None = None ) → Tensor [source] as_real¶

Transform a complex tensor to a real tensor.

The data type of the input tensor is ‘complex64’ or ‘complex128’, and the data type of the returned tensor is ‘float32’ or ‘float64’, respectively.

When the shape of the input tensor is (*, ), (* means arbitrary shape), the shape of the output tensor is (*, 2), i.e. the shape of the output is the shape of the input appended by an extra 2.

Parameters

x (Tensor) – The input tensor. Data type is ‘complex64’ or ‘complex128’.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, The output. Data type is ‘float32’ or ‘float64’, with the same precision as the input.

Examples

>>> import paddle
>>> x = paddle.arange(12, dtype=paddle.float32).reshape([2, 3, 2])
>>> y = paddle.as_complex(x)
>>> z = paddle.as_real(y)
>>> print(z)
Tensor(shape=[2, 3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[0. , 1. ],
 [2. , 3. ],
 [4. , 5. ]],
[[6. , 7. ],
 [8. , 9. ],
 [10., 11.]]])

as_strided ( shape: Sequence[int], stride: Sequence[int], offset: int = 0, name: str | None = None ) → Tensor [source] as_strided¶

View x with specified shape, stride and offset.

Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode.

The following image illustrates an example: transforming an input Tensor with shape [2,4,6] into a Tensor with shape [8,6] and stride [6,1].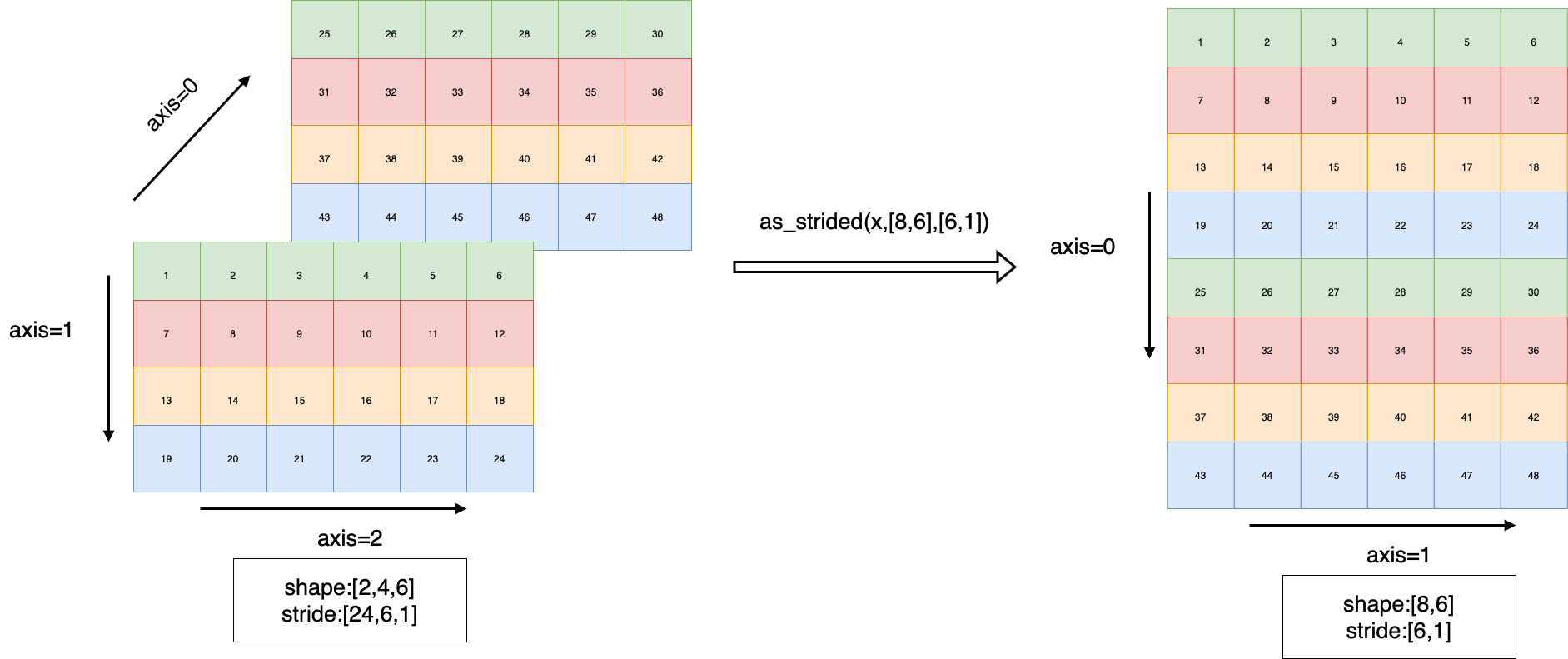

Parameters

x (Tensor) – An N-D Tensor. The data type is float32, float64, int32, int64 or bool
shape (list|tuple) – Define the target shape. Each element of it should be integer.
stride (list|tuple) – Define the target stride. Each element of it should be integer.
offset (int, optional) – Define the target Tensor’s offset from x’s holder. Default: 0.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A as_strided Tensor with the same data type as x.

Examples

>>> import paddle
>>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True})

>>> x = paddle.rand([2, 4, 6], dtype="float32")

>>> out = paddle.as_strided(x, [8, 6], [6, 1])
>>> print(out.shape)
[8, 6]
>>> # the stride is [6, 1].

asin ( name: str | None = None ) → Tensor [source] asin¶

Arcsine Operator.

\[out = sin^{-1}(x)\]

Parameters

x (Tensor) – Input of Asin operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Same shape and dtype as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.asin(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.41151685, -0.20135793,  0.10016742,  0.30469266])

asin_ ( name=None ) asin_¶: Inplace version of asin API, the output Tensor will be inplaced with input x. Please refer to asin.

asinh ( name: str | None = None ) → Tensor [source] asinh¶

Asinh Activation Operator.

\[out = asinh(x)\]

Parameters

x (Tensor) – Input of Asinh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Asinh operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.asinh(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.39003533, -0.19869010,  0.09983408,  0.29567307])

asinh_ ( name=None ) asinh_¶: Inplace version of asinh API, the output Tensor will be inplaced with input x. Please refer to asinh.

astype ( dtype: DTypeLike ) → Tensor astype¶

Cast a Tensor to a specified data type if it differs from the current dtype; otherwise, return the original Tensor.

Parameters: dtype – The target data type.
Returns: a new Tensor with target dtype
Return type: Tensor

Examples

>>> import paddle
>>> import numpy as np

>>> original_tensor = paddle.ones([2, 2])
>>> print("original tensor's dtype is: {}".format(original_tensor.dtype))
original tensor's dtype is: paddle.float32
>>> new_tensor = original_tensor.astype('float32')
>>> print("new tensor's dtype is: {}".format(new_tensor.dtype))
new tensor's dtype is: paddle.float32

atan ( name: str | None = None ) → Tensor [source] atan¶

Arctangent Operator.

\[out = tan^{-1}(x)\]

Parameters

x (Tensor) – Input of Atan operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Same shape and dtype as input x: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.atan(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.38050640, -0.19739556,  0.09966865,  0.29145682])

atan2 ( y: Tensor, name: str | None = None ) → Tensor [source] atan2¶

Element-wise arctangent of x/y with consideration of the quadrant.

Equation:: \[\begin{split}atan2(x,y)=\left\{\begin{matrix} & tan^{-1}(\frac{x}{y}) & y > 0 \\ & tan^{-1}(\frac{x}{y}) + \pi & x>=0, y < 0 \\ & tan^{-1}(\frac{x}{y}) - \pi & x<0, y < 0 \\ & +\frac{\pi}{2} & x>0, y = 0 \\ & -\frac{\pi}{2} & x<0, y = 0 \\ &\text{undefined} & x=0, y = 0 \end{matrix}\right.\end{split}\]

Parameters

x (Tensor) – An N-D Tensor, the data type is int32, int64, float16, float32, float64.
y (Tensor) – An N-D Tensor, must have the same type as x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor, the shape and data type is the same with input (The output data type is float64 when the input data type is int).

Return type

out (Tensor)

Examples

>>> import paddle

>>> x = paddle.to_tensor([-1, +1, +1, -1]).astype('float32')
>>> x
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-1,  1,  1, -1])

>>> y = paddle.to_tensor([-1, -1, +1, +1]).astype('float32')
>>> y
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-1,  -1,  1, 1])

>>> out = paddle.atan2(x, y)
>>> out
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-2.35619450,  2.35619450,  0.78539819, -0.78539819])

atan_ ( name=None ) atan_¶: Inplace version of atan API, the output Tensor will be inplaced with input x. Please refer to atan.

atanh ( name: str | None = None ) → Tensor [source] atanh¶

Atanh Activation Operator.

\[out = atanh(x)\]

Parameters

x (Tensor) – Input of Atan operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Atanh operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.atanh(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.42364895, -0.20273255,  0.10033534,  0.30951962])

atanh_ ( name=None ) atanh_¶: Inplace version of atanh API, the output Tensor will be inplaced with input x. Please refer to atanh.

atleast_1d ( *, name=None ) [source] atleast_1d¶

Convert inputs to tensors and return the view with at least 1-dimension. Scalar inputs are converted, one or high-dimensional inputs are preserved.

Parameters

inputs (list[Tensor]) – One or more tensors. The data type is float16, float32, float64, int16, int32, int64, int8, uint8, complex64, complex128, bfloat16 or bool.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

One Tensor, if there is only one input. List of Tensors, if there are more than one inputs.

Examples

>>> import paddle

>>> # one input
>>> x = paddle.to_tensor(123, dtype='int32')
>>> out = paddle.atleast_1d(x)
>>> print(out)
Tensor(shape=[1], dtype=int32, place=Place(cpu), stop_gradient=True,
[123])

>>> # more than one inputs
>>> x = paddle.to_tensor(123, dtype='int32')
>>> y = paddle.to_tensor([1.23], dtype='float32')
>>> out = paddle.atleast_1d(x, y)
>>> print(out)
[Tensor(shape=[1], dtype=int32, place=Place(cpu), stop_gradient=True,
[123]), Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.23000002])]

>>> # more than 1-D input
>>> x = paddle.to_tensor(123, dtype='int32')
>>> y = paddle.to_tensor([[1.23]], dtype='float32')
>>> out = paddle.atleast_1d(x, y)
>>> print(out)
[Tensor(shape=[1], dtype=int32, place=Place(cpu), stop_gradient=True,
[123]), Tensor(shape=[1, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.23000002]])]

atleast_2d ( *, name=None ) [source] atleast_2d¶

Convert inputs to tensors and return the view with at least 2-dimension. Two or high-dimensional inputs are preserved.

The following diagram illustrates the behavior of atleast_2d on different dimensional inputs for the following cases:

A 0-dim tensor input.

A 0-dim tensor and a 1-dim tensor input.

A 0-dim tensor and a 3-dim tensor input.

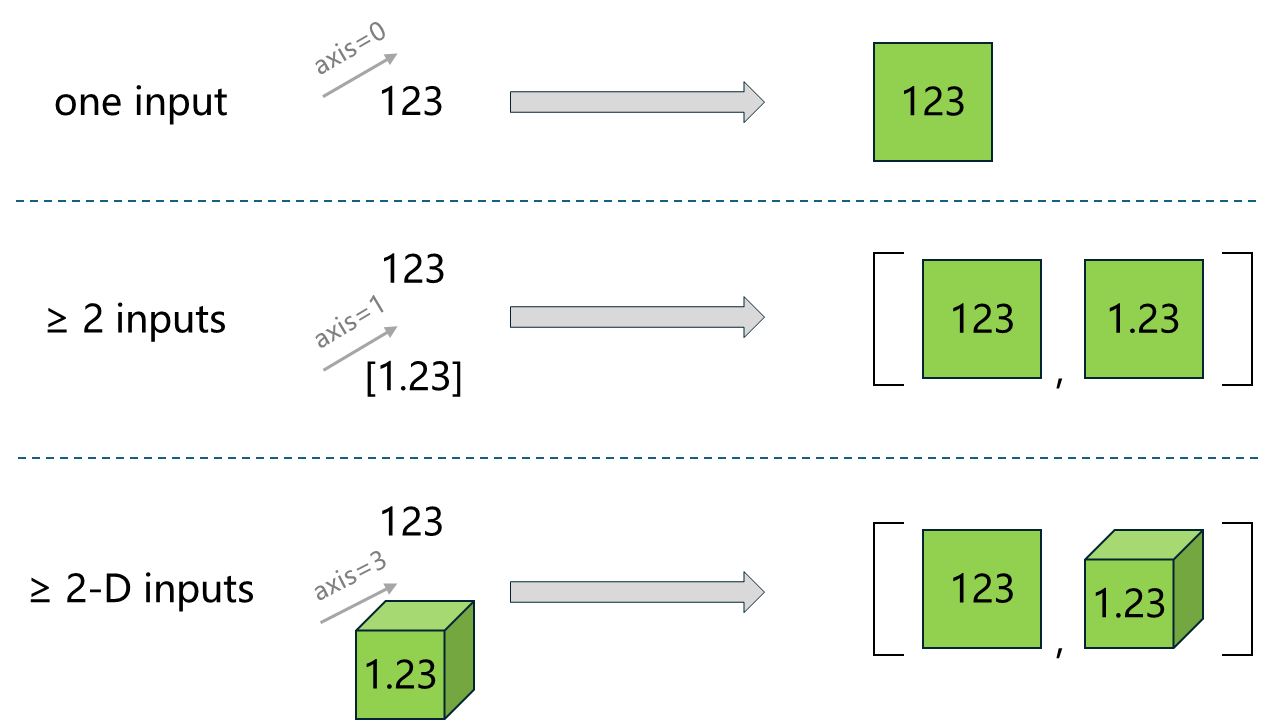
In each case, the function returns the tensors (or a list of tensors) in views with at least 2 dimensions.

Parameters

inputs (Tensor|list(Tensor)) – One or more tensors. The data type is float16, float32, float64, int16, int32, int64, int8, uint8, complex64, complex128, bfloat16 or bool.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

One Tensor, if there is only one input. List of Tensors, if there are more than one inputs.

Examples

>>> import paddle

>>> # one input
>>> x = paddle.to_tensor(123, dtype='int32')
>>> out = paddle.atleast_2d(x)
>>> print(out)
Tensor(shape=[1, 1], dtype=int32, place=Place(cpu), stop_gradient=True,
[[123]])

>>> # more than one inputs
>>> x = paddle.to_tensor(123, dtype='int32')
>>> y = paddle.to_tensor([1.23], dtype='float32')
>>> out = paddle.atleast_2d(x, y)
>>> print(out)
[Tensor(shape=[1, 1], dtype=int32, place=Place(cpu), stop_gradient=True,
[[123]]), Tensor(shape=[1, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.23000002]])]

>>> # more than 2-D input
>>> x = paddle.to_tensor(123, dtype='int32')
>>> y = paddle.to_tensor([[[1.23]]], dtype='float32')
>>> out = paddle.atleast_2d(x, y)
>>> print(out)
[Tensor(shape=[1, 1], dtype=int32, place=Place(cpu), stop_gradient=True,
[[123]]), Tensor(shape=[1, 1, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[1.23000002]]])]

atleast_3d ( *, name=None ) [source] atleast_3d¶

Convert inputs to tensors and return the view with at least 3-dimension. Three or high-dimensional inputs are preserved.

Parameters

inputs (Tensor|list(Tensor)) – One or more tensors. The data type is float16, float32, float64, int16, int32, int64, int8, uint8, complex64, complex128, bfloat16 or bool.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

One Tensor, if there is only one input. List of Tensors, if there are more than one inputs.

Examples

>>> import paddle

>>> # one input
>>> x = paddle.to_tensor(123, dtype='int32')
>>> out = paddle.atleast_3d(x)
>>> print(out)
Tensor(shape=[1, 1, 1], dtype=int32, place=Place(cpu), stop_gradient=True,
[[[123]]])

>>> # more than one inputs
>>> x = paddle.to_tensor(123, dtype='int32')
>>> y = paddle.to_tensor([1.23], dtype='float32')
>>> out = paddle.atleast_3d(x, y)
>>> print(out)
[Tensor(shape=[1, 1, 1], dtype=int32, place=Place(cpu), stop_gradient=True,
[[[123]]]), Tensor(shape=[1, 1, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[1.23000002]]])]

>>> # more than 3-D input
>>> x = paddle.to_tensor(123, dtype='int32')
>>> y = paddle.to_tensor([[[[1.23]]]], dtype='float32')
>>> out = paddle.atleast_3d(x, y)
>>> print(out)
[Tensor(shape=[1, 1, 1], dtype=int32, place=Place(cpu), stop_gradient=True,
[[[123]]]), Tensor(shape=[1, 1, 1, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[[1.23000002]]]])]

backward ( grad_tensor: Tensor | None = None, retain_graph: bool = False ) → None backward¶

Run backward of current Graph which starts from current Tensor.

The new gradient will accumulate on previous gradient.

You can clear gradient by Tensor.clear_grad() .

Parameters

grad_tensor (Tensor|None, optional) – initial gradient values of the current Tensor. If grad_tensor is None, the initial gradient values of the current Tensor would be Tensor filled with 1.0; if grad_tensor is not None, it must have the same length as the current Tensor. The default value is None.
retain_graph (bool, optional) – If False, the graph used to compute grads will be freed. If you would like to add more ops to the built graph after calling this method( backward ), set the parameter retain_graph to True, then the grads will be retained. Thus, setting it to False is much more memory-efficient. Defaults to False.

Returns

None

Examples

>>> import paddle
>>> x = paddle.to_tensor(5., stop_gradient=False)
>>> for i in range(5):
...     y = paddle.pow(x, 4.0)
...     y.backward()
...     print("{}: {}".format(i, x.grad))
0: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
500.)
1: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
1000.)
2: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
1500.)
3: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
2000.)
4: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
2500.)

>>> x.clear_grad()
>>> print("{}".format(x.grad))
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
0.)

>>> grad_tensor=paddle.to_tensor(2.)
>>> for i in range(5):
...     y = paddle.pow(x, 4.0)
...     y.backward(grad_tensor)
...     print("{}: {}".format(i, x.grad))
0: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
1000.)
1: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
2000.)
2: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
3000.)
3: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
4000.)
4: Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
5000.)

baddbmm ( x: Tensor, y: Tensor, beta: float = 1.0, alpha: float = 1.0, name: str | None = None ) → Tensor [source] baddbmm¶

baddbmm

Perform batch matrix multiplication for input $x$ and $y$. $input$ is added to the final result. The equation is:

\[Out = alpha * x * y + beta * input\]

$Input$, $x$ and $y$ can carry the LoD (Level of Details) information, or not. But the output only shares the LoD information with input $input$.

Parameters

input (Tensor) – The input Tensor to be added to the final result.
x (Tensor) – The first input Tensor for batch matrix multiplication.
y (Tensor) – The second input Tensor for batch matrix multiplication.
beta (float, optional) – Coefficient of $input$, default is 1.
alpha (float, optional) – Coefficient of $x*y$, default is 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output Tensor of baddbmm.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.ones([2, 2, 2])
>>> y = paddle.ones([2, 2, 2])
>>> input = paddle.ones([2, 2, 2])

>>> out = paddle.baddbmm(input=input, x=x, y=y, beta=0.5, alpha=5.0)

>>> out
Tensor(shape=[2, 2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[10.50000000, 10.50000000],
  [10.50000000, 10.50000000]],
 [[10.50000000, 10.50000000],
  [10.50000000, 10.50000000]]])

baddbmm_ ( x: Tensor, y: Tensor, beta: float = 1.0, alpha: float = 1.0, name: str | None = None ) → Tensor [source] baddbmm_¶: Inplace version of baddbmm API, the output Tensor will be inplaced with input input. Please refer to baddbmm.

bernoulli_ ( p: float | Tensor = 0.5, name: str | None = None ) → Tensor [source] bernoulli_¶

This is the inplace version of api bernoulli, which returns a Tensor filled with random values sampled from a bernoulli distribution. The output Tensor will be inplaced with input x. Please refer to bernoulli.

Parameters

x (Tensor) – The input tensor to be filled with random values.
p (float|Tensor, optional) – The success probability parameter of the output Tensor’s bernoulli distribution. If p is float, all elements of the output Tensor shared the same success probability. If p is a Tensor, it has per-element success probabilities, and the shape should be broadcastable to x. Default is 0.5
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, A Tensor filled with random values sampled from the bernoulli distribution with success probability p .

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> paddle.seed(200)
>>> x = paddle.randn([3, 4])
>>> x.bernoulli_()
>>> print(x)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 1., 0., 1.],
 [1., 1., 0., 1.],
 [0., 1., 0., 0.]])

>>> x = paddle.randn([3, 4])
>>> p = paddle.randn([3, 1])
>>> x.bernoulli_(p)
>>> print(x)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 1., 1., 1.],
 [0., 0., 0., 0.],
 [0., 0., 0., 0.]])

bincount ( weights: Tensor | None = None, minlength: int = 0, name: str | None = None ) → Tensor [source] bincount¶

Computes frequency of each value in the input tensor.

Parameters

x (Tensor) – A Tensor with non-negative integer. Should be 1-D tensor.
weights (Tensor, optional) – Weight for each value in the input tensor. Should have the same shape as input. Default is None.
minlength (int, optional) – Minimum number of bins. Should be non-negative integer. Default is 0.
name (str|None, optional) – Normally there is no need for user to set this property. For more information, please refer to Name. Default is None.

Returns

The tensor of frequency.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 1, 4, 5])
>>> result1 = paddle.bincount(x)
>>> print(result1)
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 2, 1, 0, 1, 1])

>>> w = paddle.to_tensor([2.1, 0.4, 0.1, 0.5, 0.5])
>>> result2 = paddle.bincount(x, weights=w)
>>> print(result2)
Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.        , 2.19999981, 0.40000001, 0.        , 0.50000000, 0.50000000])

bitwise_and ( y: Tensor, out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_and¶

Apply bitwise_and on Tensor X and Y .

\[Out = X \& Y\]

Note

paddle.bitwise_and supports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .

Parameters

x (Tensor) – Input Tensor of bitwise_and . It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
y (Tensor) – Input Tensor of bitwise_and . It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
out (Tensor|None, optional) – Result of bitwise_and . It is a N-D Tensor with the same data type of input Tensor. Default: None.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Result of bitwise_and . It is a N-D Tensor with the same data type of input Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([-5, -1, 1])
>>> y = paddle.to_tensor([4,  2, -3])
>>> res = paddle.bitwise_and(x, y)
>>> print(res)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 2, 1])

bitwise_and_ ( y: Tensor, name: str | None = None ) → Tensor [source] bitwise_and_¶: Inplace version of bitwise_and API, the output Tensor will be inplaced with input x. Please refer to bitwise_and.

bitwise_invert ( out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_invert¶

Apply bitwise_not (bitwise inversion) on Tensor x.

This is an alias to the paddle.bitwise_not function.

\[Out = \sim X\]

Note

paddle.bitwise_invert is functionally equivalent to paddle.bitwise_not.

Parameters

x (Tensor) – Input Tensor of bitwise_invert. It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
out (Tensor|None, optional) – Result of bitwise_invert. It is a N-D Tensor with the same data type as the input Tensor. Default: None.
name (str|None, optional) – The default value is None. This property is typically not set by the user. For more information, please refer to Name.

Returns

Result of bitwise_invert. It is a N-D Tensor with the same data type as the input Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([-5, -1, 1])
>>> res = x.bitwise_invert()
>>> print(res)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[ 4,  0, -2])

bitwise_invert_ ( name: str | None = None ) → Tensor [source] bitwise_invert_¶: Inplace version of bitwise_invert API, the output Tensor will be inplaced with input x. Please refer to bitwise_invert_.

bitwise_left_shift ( y: Tensor, is_arithmetic: bool = True, out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_left_shift¶

Apply bitwise_left_shift on Tensor X and Y .

\[Out = X \ll Y\]

Note

paddle.bitwise_left_shift supports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .

Parameters

x (Tensor) – Input Tensor of bitwise_left_shift . It is a N-D Tensor of uint8, int8, int16, int32, int64.
y (Tensor) – Input Tensor of bitwise_left_shift . It is a N-D Tensor of uint8, int8, int16, int32, int64.
is_arithmetic (bool, optional) – A boolean indicating whether to choose arithmetic shift, if False, means logic shift. Default True.
out (Tensor|None, optional) – Result of bitwise_left_shift . It is a N-D Tensor with the same data type of input Tensor. Default: None.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Result of bitwise_left_shift . It is a N-D Tensor with the same data type of input Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([[1,2,4,8],[16,17,32,65]])
>>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]])
>>> paddle.bitwise_left_shift(x, y, is_arithmetic=True)
Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [[2  , 8  , 32 , 128],
        [64 , 136, 128, 130]])

>>> import paddle
>>> x = paddle.to_tensor([[1,2,4,8],[16,17,32,65]])
>>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]])
>>> paddle.bitwise_left_shift(x, y, is_arithmetic=False)
Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
    [[2  , 8  , 32 , 128],
        [64 , 136, 128, 130]])

bitwise_left_shift_ ( y: Tensor, is_arithmetic: bool = True, out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_left_shift_¶: Inplace version of bitwise_left_shift API, the output Tensor will be inplaced with input x. Please refer to bitwise_left_shift.

bitwise_not ( out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_not¶

Apply bitwise_not on Tensor X.

\[Out = \sim X\]

Note

paddle.bitwise_not supports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .

Parameters

x (Tensor) – Input Tensor of bitwise_not . It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
out (Tensor|None, optional) – Result of bitwise_not . It is a N-D Tensor with the same data type of input Tensor. Default: None.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Result of bitwise_not . It is a N-D Tensor with the same data type of input Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([-5, -1, 1])
>>> res = paddle.bitwise_not(x)
>>> print(res)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[ 4,  0, -2])

bitwise_not_ ( name: str | None = None ) → Tensor [source] bitwise_not_¶: Inplace version of bitwise_not API, the output Tensor will be inplaced with input x. Please refer to bitwise_not.

bitwise_or ( y: Tensor, out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_or¶

Apply bitwise_or on Tensor X and Y .

\[Out = X | Y\]

Note

paddle.bitwise_or supports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .

Parameters

x (Tensor) – Input Tensor of bitwise_or . It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
y (Tensor) – Input Tensor of bitwise_or . It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
out (Tensor|None, optional) – Result of bitwise_or . It is a N-D Tensor with the same data type of input Tensor. Default: None.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Result of bitwise_or . It is a N-D Tensor with the same data type of input Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([-5, -1, 1])
>>> y = paddle.to_tensor([4,  2, -3])
>>> res = paddle.bitwise_or(x, y)
>>> print(res)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[-1, -1, -3])

bitwise_or_ ( y: Tensor, name: str | None = None ) → Tensor [source] bitwise_or_¶: Inplace version of bitwise_or API, the output Tensor will be inplaced with input x. Please refer to bitwise_or.

bitwise_right_shift ( y: Tensor, is_arithmetic: bool = True, out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_right_shift¶

Apply bitwise_right_shift on Tensor X and Y .

\[Out = X \gg Y\]

Note

paddle.bitwise_right_shift supports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .

Parameters

x (Tensor) – Input Tensor of bitwise_right_shift . It is a N-D Tensor of uint8, int8, int16, int32, int64.
y (Tensor) – Input Tensor of bitwise_right_shift . It is a N-D Tensor of uint8, int8, int16, int32, int64.
is_arithmetic (bool, optional) – A boolean indicating whether to choose arithmetic shift, if False, means logic shift. Default True.
out (Tensor|None, optional) – Result of bitwise_right_shift . It is a N-D Tensor with the same data type of input Tensor. Default: None.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Result of bitwise_right_shift . It is a N-D Tensor with the same data type of input Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([[10,20,40,80],[16,17,32,65]])
>>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]])
>>> paddle.bitwise_right_shift(x, y, is_arithmetic=True)
Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [[5 , 5 , 5 , 5 ],
        [4 , 2 , 8 , 32]])

>>> import paddle
>>> x = paddle.to_tensor([[-10,-20,-40,-80],[-16,-17,-32,-65]], dtype=paddle.int8)
>>> y = paddle.to_tensor([[1,2,3,4,], [2,3,2,1]], dtype=paddle.int8)
>>> paddle.bitwise_right_shift(x, y, is_arithmetic=False)  # logic shift
Tensor(shape=[2, 4], dtype=int8, place=Place(gpu:0), stop_gradient=True,
    [[123, 59 , 27 , 11 ],
        [60 , 29 , 56 , 95 ]])

bitwise_right_shift_ ( y: Tensor, is_arithmetic: bool = True, out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_right_shift_¶: Inplace version of bitwise_right_shift API, the output Tensor will be inplaced with input x. Please refer to bitwise_left_shift.

bitwise_xor ( y: Tensor, out: Tensor | None = None, name: str | None = None ) → Tensor [source] bitwise_xor¶

Apply bitwise_xor on Tensor X and Y .

\[Out = X ^\wedge Y\]

Note

paddle.bitwise_xor supports broadcasting. If you want know more about broadcasting, please refer to please refer to Introduction to Tensor .

Parameters

x (Tensor) – Input Tensor of bitwise_xor . It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
y (Tensor) – Input Tensor of bitwise_xor . It is a N-D Tensor of bool, uint8, int8, int16, int32, int64.
out (Tensor|None, optional) – Result of bitwise_xor . It is a N-D Tensor with the same data type of input Tensor. Default: None.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Result of bitwise_xor . It is a N-D Tensor with the same data type of input Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([-5, -1, 1])
>>> y = paddle.to_tensor([4,  2, -3])
>>> res = paddle.bitwise_xor(x, y)
>>> print(res)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[-1, -3, -4])

bitwise_xor_ ( y: Tensor, name: str | None = None ) → Tensor [source] bitwise_xor_¶: Inplace version of bitwise_xor API, the output Tensor will be inplaced with input x. Please refer to bitwise_xor.

block_diag ( name: str | None = None ) → Tensor [source] block_diag¶

Create a block diagonal matrix from provided tensors.

Parameters

inputs (list|tuple) – inputs is a Tensor list or Tensor tuple, one or more tensors with 0, 1, or 2 dimensions. The data type: bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None).

Returns

Tensor, A Tensor. The data type is same as inputs.

Examples

>>> import paddle

>>> A = paddle.to_tensor([[4], [3], [2]])
>>> B = paddle.to_tensor([7, 6, 5])
>>> C = paddle.to_tensor(1)
>>> D = paddle.to_tensor([[5, 4, 3], [2, 1, 0]])
>>> E = paddle.to_tensor([[8, 7], [7, 8]])
>>> out = paddle.block_diag([A, B, C, D, E])
>>> print(out)
Tensor(shape=[9, 10], dtype=int64, place=Place(gpu:0), stop_gradient=True,
    [[4, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [3, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [2, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 7, 6, 5, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 5, 4, 3, 0, 0],
    [0, 0, 0, 0, 0, 2, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 8, 7],
    [0, 0, 0, 0, 0, 0, 0, 0, 7, 8]])

bmm ( y: Tensor, name: str | None = None ) → Tensor [source] bmm¶

Applies batched matrix multiplication to two tensors.

Both of the two input tensors must be three-dimensional and share the same batch size.

If x is a (b, m, k) tensor, y is a (b, k, n) tensor, the output will be a (b, m, n) tensor.

Parameters

x (Tensor) – The input Tensor.
y (Tensor) – The input Tensor.
name (str|None) – A name for this layer(optional). If set None, the layer will be named automatically. Default: None.

Returns

The product Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> # In imperative mode:
>>> # size x: (2, 2, 3) and y: (2, 3, 2)
>>> x = paddle.to_tensor([[[1.0, 1.0, 1.0],
...                     [2.0, 2.0, 2.0]],
...                     [[3.0, 3.0, 3.0],
...                     [4.0, 4.0, 4.0]]])
>>> y = paddle.to_tensor([[[1.0, 1.0],[2.0, 2.0],[3.0, 3.0]],
...                     [[4.0, 4.0],[5.0, 5.0],[6.0, 6.0]]])
>>> out = paddle.bmm(x, y)
>>> print(out)
Tensor(shape=[2, 2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[6. , 6. ],
  [12., 12.]],
 [[45., 45.],
  [60., 60.]]])

broadcast_shape ( y_shape: Sequence[int] ) → list[int] [source] broadcast_shape¶

The function returns the shape of doing operation with broadcasting on tensors of x_shape and y_shape.

Note

If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x_shape (list[int]|tuple[int]) – A shape of tensor.
y_shape (list[int]|tuple[int]) – A shape of tensor.

Returns

list[int], the result shape.

Examples

>>> import paddle

>>> shape = paddle.broadcast_shape([2, 1, 3], [1, 3, 1])
>>> shape
[2, 3, 3]

>>> # shape = paddle.broadcast_shape([2, 1, 3], [3, 3, 1])
>>> # ValueError (terminated with error message).

broadcast_tensors ( name: str | None = None ) → list[Tensor] [source] broadcast_tensors¶

Broadcast a list of tensors following broadcast semantics

Note

If you want know more about broadcasting, please refer to Introduction to Tensor .

The following figure illustrates the process of broadcasting three tensors to the same dimensions. The dimensions of the three tensors are [4, 1, 3], [2, 3], and [4, 2, 1], respectively. During broadcasting, alignment starts from the last dimension, and for each dimension, either the sizes of the two tensors in that dimension are equal, or one of the tensors has a dimension of 1, or one of the tensors lacks that dimension. In the figure below, in the last dimension, Tensor3 has a size of 1, while Tensor1 and Tensor2 have sizes of 3; thus, this dimension is expanded to 3 for all tensors. In the second-to-last dimension, Tensor1 has a size of 2, and Tensor2 and Tensor3 both have sizes of 2; hence, this dimension is expanded to 2 for all tensors. In the third-to-last dimension, Tensor2 lacks this dimension, while Tensor1 and Tensor3 have sizes of 4; consequently, this dimension is expanded to 4 for all tensors. Ultimately, all tensors are expanded to [4, 2, 3].

Parameters

input (list|tuple) – input is a Tensor list or Tensor tuple which is with data type bool, float16, float32, float64, int32, int64, complex64, complex128. All the Tensors in input must have same data type. Currently we only support tensors with rank no greater than 5.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

list(Tensor), The list of broadcasted tensors following the same order as input.

Examples

>>> import paddle
>>> x1 = paddle.rand([1, 2, 3, 4]).astype('float32')
>>> x2 = paddle.rand([1, 2, 1, 4]).astype('float32')
>>> x3 = paddle.rand([1, 1, 3, 1]).astype('float32')
>>> out1, out2, out3 = paddle.broadcast_tensors(input=[x1, x2, x3])
>>> # out1, out2, out3: tensors broadcasted from x1, x2, x3 with shape [1,2,3,4]

broadcast_to ( shape: ShapeLike, name: str | None = None ) → Tensor [source] broadcast_to¶

Broadcast the input tensor to a given shape.

Both the number of dimensions of x and the number of elements in shape should be less than or equal to 6. The dimension to broadcast to must have a value 0.

The following figure shows the process of broadcasting a one-dimensional tensor of shape [3] to a two-dimensional tensor of shape [2,3] based on the shape specified by ‘shape’.

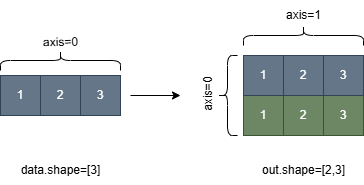
Parameters

x (Tensor) – The input tensor, its data type is bool, float16, float32, float64, int32, int64, uint8 or uint16.
shape (list|tuple|Tensor) – The result shape after broadcasting. The data type is int32. If shape is a list or tuple, all its elements should be integers or 0-D or 1-D Tensors with the data type int32. If shape is a Tensor, it should be an 1-D Tensor with the data type int32. The value -1 in shape means keeping the corresponding dimension unchanged.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor, A Tensor with the given shape. The data type is the same as x.

Examples

>>> import paddle

>>> data = paddle.to_tensor([1, 2, 3], dtype='int32')
>>> out = paddle.broadcast_to(data, shape=[2, 3])
>>> print(out)
Tensor(shape=[2, 3], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 2, 3],
 [1, 2, 3]])

bucketize ( sorted_sequence: Tensor, out_int32: bool = False, right: bool = False, name: str | None = None ) → Tensor [source] bucketize¶

This API is used to find the index of the corresponding 1D tensor sorted_sequence in the innermost dimension based on the given x.

Parameters

x (Tensor) – An input N-D tensor value with type int32, int64, float32, float64.
sorted_sequence (Tensor) – An input 1-D tensor with type int32, int64, float32, float64. The value of the tensor monotonically increases in the innermost dimension.
out_int32 (bool, optional) – Data type of the output tensor which can be int32, int64. The default value is False, and it indicates that the output data type is int64.
right (bool, optional) – Find the upper or lower bounds of the sorted_sequence range in the innermost dimension based on the given x. If the value of the sorted_sequence is nan or inf, return the size of the innermost dimension. The default value is False and it shows the lower bounds.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor (the same sizes of the x), return the tensor of int32 if set out_int32 is True, otherwise return the tensor of int64.

Examples

>>> import paddle

>>> sorted_sequence = paddle.to_tensor([2, 4, 8, 16], dtype='int32')
>>> x = paddle.to_tensor([[0, 8, 4, 16], [-1, 2, 8, 4]], dtype='int32')
>>> out1 = paddle.bucketize(x, sorted_sequence)
>>> print(out1)
Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 2, 1, 3],
 [0, 0, 2, 1]])
>>> out2 = paddle.bucketize(x, sorted_sequence, right=True)
>>> print(out2)
Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 3, 2, 4],
 [0, 1, 3, 2]])
>>> out3 = x.bucketize(sorted_sequence)
>>> print(out3)
Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 2, 1, 3],
 [0, 0, 2, 1]])
>>> out4 = x.bucketize(sorted_sequence, right=True)
>>> print(out4)
Tensor(shape=[2, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 3, 2, 4],
 [0, 1, 3, 2]])

cast ( dtype: DTypeLike ) → Tensor [source] cast¶

Take in the Tensor x with x.dtype and cast it to the output with dtype. It’s meaningless if the output dtype equals the input dtype, but it’s fine if you do so.

The following picture shows an example where a tensor of type float64 is cast to a tensor of type uint8.

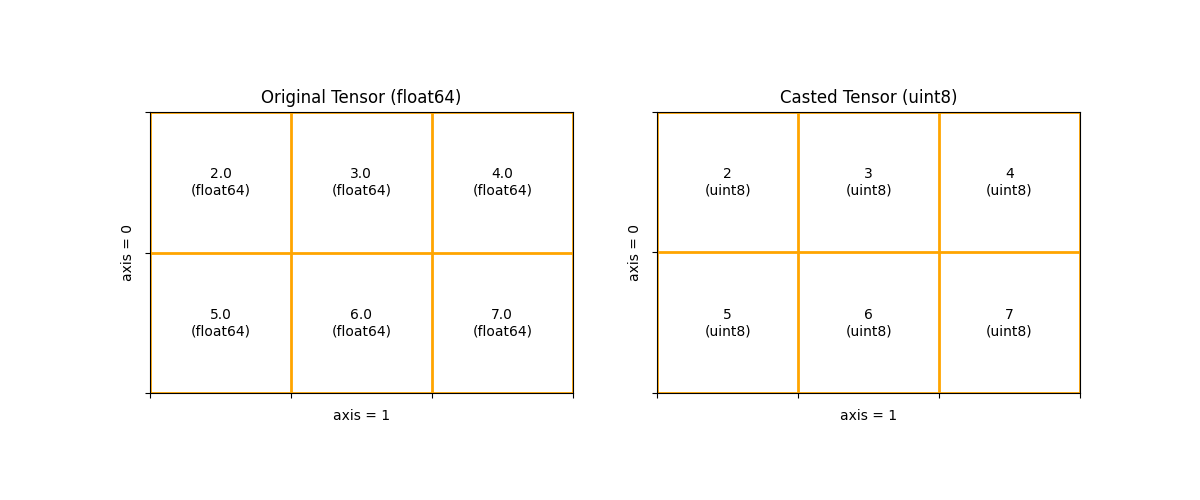
Parameters

x (Tensor) – An input N-D Tensor with data type bool, float16, float32, float64, int32, int64, uint8.
dtype (paddle.dtype|np.dtype|str) – Data type of the output: bool, float16, float32, float64, int8, int32, int64, uint8.

Returns

Tensor, A Tensor with the same shape as input’s.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 4], 'float64')
>>> y = paddle.cast(x, 'uint8')

cast_ ( dtype: DTypeLike ) → Tensor [source] cast_¶: Inplace version of cast API, the output Tensor will be inplaced with input x. Please refer to cast.

cauchy_ ( loc: Numeric = 0, scale: Numeric = 1, name: str | None = None ) → paddle.Tensor [source] cauchy_¶

Fills the tensor with numbers drawn from the Cauchy distribution.

Parameters

x (Tensor) – the tensor will be filled, The data type is float32 or float64.
loc (scalar, optional) – Location of the peak of the distribution. The data type is float32 or float64.
scale (scalar, optional) – The half-width at half-maximum (HWHM). The data type is float32 or float64. Must be positive values.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

input tensor with numbers drawn from the Cauchy distribution.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.randn([3, 4])
>>> x.cauchy_(1, 2)
>>> 
>>> print(x)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 3.80087137,  2.25415039,  2.77960515,  7.64125967],
 [ 0.76541221,  2.74023032,  1.99383152, -0.12685823],
 [ 1.45228469,  1.76275957, -4.30458832, 34.74880219]])

cdist ( y: Tensor, p: float = 2.0, compute_mode: Literal['use_mm_for_euclid_dist_if_necessary', 'use_mm_for_euclid_dist', 'donot_use_mm_for_euclid_dist'] = 'use_mm_for_euclid_dist_if_necessary', name: str | None = None ) → Tensor [source] cdist¶

Compute the p-norm distance between each pair of the two collections of inputs.

This function is equivalent to scipy.spatial.distance.cdist(input,’minkowski’, p=p) if $p \in (0, \infty)$. When $p = 0$ it is equivalent to scipy.spatial.distance.cdist(input, ‘hamming’) * M. When $p = \infty$, the closest scipy function is scipy.spatial.distance.cdist(xn, lambda x, y: np.abs(x - y).max()).

Parameters

x (Tensor) – A tensor with shape $B \times P \times M$.
y (Tensor) – A tensor with shape $B \times R \times M$.
p (float, optional) – The value for the p-norm distance to calculate between each vector pair. Default: $2.0$.
compute_mode (str, optional) –
The mode for compute distance.
- use_mm_for_euclid_dist_if_necessary , for p = 2.0 and (P > 25 or R > 25), it will use matrix multiplication to calculate euclid distance if possible.
- use_mm_for_euclid_dist , for p = 2.0, it will use matrix multiplication to calculate euclid distance.
- donot_use_mm_for_euclid_dist , it will not use matrix multiplication to calculate euclid distance.
Default: use_mm_for_euclid_dist_if_necessary.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, the dtype is same as input tensor.

If x has shape $B \times P \times M$ and y has shape $B \times R \times M$ then the output will have shape $B \times P \times R$.

Examples

>>> import paddle
>>> x = paddle.to_tensor([[0.9041,  0.0196], [-0.3108, -2.4423], [-0.4821,  1.059]], dtype=paddle.float32)
>>> y = paddle.to_tensor([[-2.1763, -0.4713], [-0.6986,  1.3702]], dtype=paddle.float32)
>>> distance = paddle.cdist(x, y)
>>> print(distance)
Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[3.11927032, 2.09589314],
 [2.71384072, 3.83217239],
 [2.28300953, 0.37910119]])

ceil ( name: str | None = None ) → Tensor [source] ceil¶

Ceil Operator. Computes ceil of x element-wise.

\[out = \left \lceil x \right \rceil\]

Parameters

x (Tensor) – Input of Ceil operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Ceil operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.ceil(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0., -0., 1. , 1. ])

ceil_ ( name=None ) ceil_¶: Inplace version of ceil API, the output Tensor will be inplaced with input x. Please refer to ceil.

cholesky ( upper: bool = False, name: str | None = None ) → Tensor [source] cholesky¶

Computes the Cholesky decomposition of one symmetric positive-definite matrix or batches of symmetric positive-definite matrices.

If upper is True, the decomposition has the form $A = U^{T}U$ , and the returned matrix $U$ is upper-triangular. Otherwise, the decomposition has the form $A = LL^{T}$ , and the returned matrix $L$ is lower-triangular.

Parameters

x (Tensor) – The input tensor. Its shape should be [*, M, M], where * is zero or more batch dimensions, and matrices on the inner-most 2 dimensions all should be symmetric positive-definite. Its data type should be float32 or float64.
upper (bool, optional) – The flag indicating whether to return upper or lower triangular matrices. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A Tensor with same shape and data type as x. It represents triangular matrices generated by Cholesky decomposition.

Examples

>>> import paddle
>>> paddle.seed(2023)

>>> a = paddle.rand([3, 3], dtype="float32")
>>> a_t = paddle.transpose(a, [1, 0])
>>> x = paddle.matmul(a, a_t) + 1e-03

>>> out = paddle.linalg.cholesky(x, upper=False)
>>> print(out)
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.04337072, 0.        , 0.        ],
 [1.06467664, 0.17859250, 0.        ],
 [1.30602181, 0.08326444, 0.22790681]])

cholesky_inverse ( upper: bool = False, name: str | None = None ) → Tensor cholesky_inverse¶

Using the Cholesky factor U to calculate the inverse matrix of a symmetric positive definite matrix, returns the matrix inv.

If upper is False, U is lower triangular matrix:

\[inv = (UU^{T})^{-1}\]

If upper is True, U is upper triangular matrix:

\[inv = (U^{T}U)^{-1}\]

Parameters

x (Tensor) – A tensor of lower or upper triangular Cholesky decompositions of symmetric matrix with shape [N, N]. The data type of the x should be one of float32, float64.
upper (bool, optional) – If upper is False, x is lower triangular matrix, or is upper triangular matrix. Default: False.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor. Computes the inverse matrix.

Examples

>>> import paddle

>>> # lower triangular matrix
>>> x = paddle.to_tensor([[3.,.0,.0], [5.,3.,.0], [-1.,1.,2.]])
>>> out = paddle.linalg.cholesky_inverse(x)
>>> print(out)
Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
[[ 0.61728382, -0.25925916,  0.22222219],
 [-0.25925916,  0.13888884, -0.08333331],
 [ 0.22222218, -0.08333331,  0.25000000]])

>>> # upper triangular matrix
>>> out = paddle.linalg.cholesky_inverse(x.T, upper=True)
>>> print(out)
Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
[[ 0.61728382, -0.25925916,  0.22222219],
 [-0.25925916,  0.13888884, -0.08333331],
 [ 0.22222218, -0.08333331,  0.25000000]])

cholesky_solve ( y: Tensor, upper: bool = False, name: str | None = None ) → Tensor cholesky_solve¶

Solves a linear system of equations A @ X = B, given A’s Cholesky factor matrix u and matrix B.

Input x and y is 2D matrices or batches of 2D matrices. If the inputs are batches, the outputs is also batches.

Parameters

x (Tensor) – Multiple right-hand sides of system of equations. Its shape should be [*, M, K], where * is zero or more batch dimensions. Its data type should be float32 or float64.
y (Tensor) – The input matrix which is upper or lower triangular Cholesky factor of square matrix A. Its shape should be [*, M, M], where * is zero or more batch dimensions. Its data type should be float32 or float64.
upper (bool, optional) – whether to consider the Cholesky factor as a lower or upper triangular matrix. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The solution of the system of equations. Its data type is the same as that of x.

Return type

Tensor

Examples

>>> import paddle

>>> u = paddle.to_tensor([[1, 1, 1],
...                       [0, 2, 1],
...                       [0, 0,-1]], dtype="float64")
>>> b = paddle.to_tensor([[0], [-9], [5]], dtype="float64")
>>> out = paddle.linalg.cholesky_solve(b, u, upper=True)

>>> print(out)
Tensor(shape=[3, 1], dtype=float64, place=Place(cpu), stop_gradient=True,
[[-2.50000000],
 [-7.        ],
 [ 9.50000000]])

chunk ( chunks: int, axis: int | Tensor = 0, name: str | None = None ) → list[Tensor] [source] chunk¶

Split the input tensor into multiple sub-Tensors.

Here are some examples to explain it.

Given a 3-D tensor x with a shape [3, 3, 3], if we split the first dimension into three equal parts, it will output a list containing three 3-D tensors with a shape of [1, 3, 3].

Given a 3-D tensor x with a shape [3, 3, 3], if we split the second dimension into three equal parts, it will output a list containing three 3-D tensors with a shape of [3, 1, 3].

Given a 3-D tensor x with a shape [3, 3, 3], if we split the third dimension into three equal parts, it will output a list containing three 3-D tensors with a shape of [3, 3, 1].

The following figure illustrates the first example.

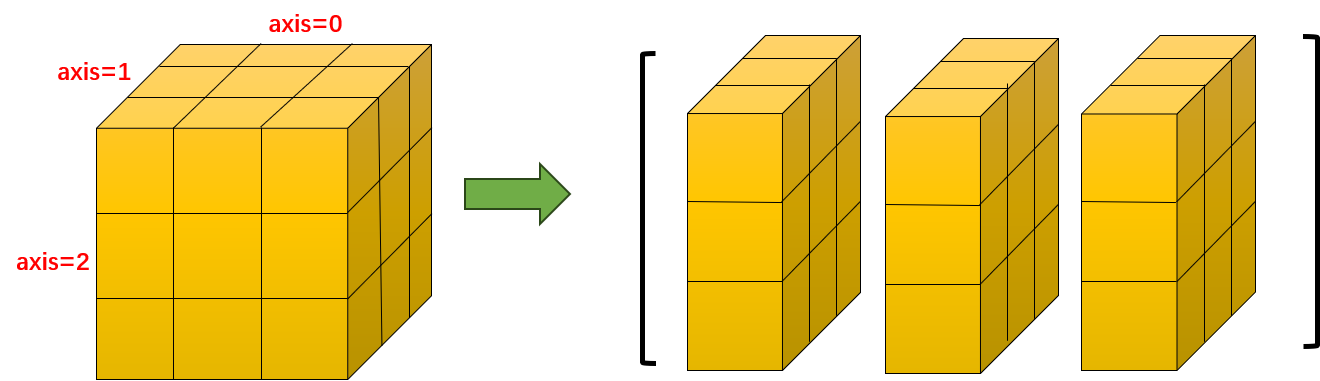
Parameters

x (Tensor) – A N-D Tensor. The data type is bool, float16, float32, float64, int32 or int64.
chunks (int) – The number of tensor to be split along the certain axis.
axis (int|Tensor, optional) – The axis along which to split, it can be a integer or a 0-D Tensor with shape [] and data type int32 or int64. If :math::axis < 0, the axis to split along is $rank(x) + axis$. Default is 0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

list(Tensor), The list of segmented Tensors.

Examples

>>> import paddle

>>> x = paddle.rand([3, 9, 5])

>>> out0, out1, out2 = paddle.chunk(x, chunks=3, axis=1)
>>> # out0.shape [3, 3, 5]
>>> # out1.shape [3, 3, 5]
>>> # out2.shape [3, 3, 5]


>>> # axis is negative, the real axis is (rank(x) + axis) which real
>>> # value is 1.
>>> out0, out1, out2 = paddle.chunk(x, chunks=3, axis=-2)
>>> # out0.shape [3, 3, 5]
>>> # out1.shape [3, 3, 5]
>>> # out2.shape [3, 3, 5]

clear_grad ( ) → None clear_grad¶: The alias of clear_gradient().

clear_gradient ( set_to_zero=True, / ) clear_gradient¶

Only for Tensor that has gradient, normally we use this for Parameters since other temporary Tensor doesn’t has gradient.

The Gradient of current Tensor will be set to 0 elementwise or None.

Parameters: set_to_zero (bool, optional) – If set to True, the gradient will be set to 0 elementwise, otherwise the gradient will be set to None. Default: True.
Returns: None.

Examples

>>> import paddle
>>> input = paddle.uniform([10, 2])
>>> linear = paddle.nn.Linear(2, 3)
>>> out = linear(input)
>>> out.backward()
>>> print("Before clear_gradient, linear.weight.grad: {}".format(linear.weight.grad))
>>> 
Before clear_gradient, linear.weight.grad: Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=False,
[[-0.03178465, -0.03178465, -0.03178465],
 [-0.98546225, -0.98546225, -0.98546225]])
>>> 
>>> linear.weight.clear_gradient()
>>> print("After clear_gradient, linear.weight.grad: {}".format(linear.weight.grad))
After clear_gradient, linear.weight.grad: Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=False,
[[0., 0., 0.],
 [0., 0., 0.]])

clip ( min: float | None = None, max: float | None = None, name: str | None = None ) → Tensor [source] clip¶

This operator clip all elements in input into the range [ min, max ] and return a resulting tensor as the following equation:

\[Out = MIN(MAX(x, min), max)\]

Parameters

x (Tensor) – An N-D Tensor with data type bfloat16, float16, float32, float64, int32 or int64.
min (float|int|Tensor, optional) – The lower bound with type float , int or a 0-D Tensor with shape [] and type bfloat16, float16, float32, float64, int32.
max (float|int|Tensor, optional) – The upper bound with type float, int or a 0-D Tensor with shape [] and type bfloat16, float16, float32, float64, int32.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

A Tensor with the same data type and data shape as input.

Return type

Tensor

Examples

>>> import paddle

>>> x1 = paddle.to_tensor([[1.2, 3.5], [4.5, 6.4]], 'float32')
>>> out1 = paddle.clip(x1, min=3.5, max=5.0)
>>> out1
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[3.50000000, 3.50000000],
 [4.50000000, 5.        ]])
>>> out2 = paddle.clip(x1, min=2.5)
>>> out2
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[2.50000000, 3.50000000],
 [4.50000000, 6.40000010]])

clip_ ( min: float | None = None, max: float | None = None, name: str | None = None ) → Tensor clip_¶: Inplace version of clip API, the output Tensor will be inplaced with input x. Please refer to clip.

clone ( ) [source] clone¶

Returns a new Tensor, which is clone of origin Tensor, and it remains in the current graph. It will always have a Tensor copy. In addition, the cloned Tensor provides gradient propagation.

Returns: Tensor, The cloned Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.0, stop_gradient=False)
>>> clone_x = x.clone()
>>> clone_x.retain_grads()
>>> y = clone_x**2
>>> y.backward()
>>> print(clone_x.stop_gradient)
False
>>> print(clone_x.grad)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False, 2.)
>>> print(x.stop_gradient)
False
>>> print(x.grad)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False, 2.)

>>> x = paddle.to_tensor(1.0)
>>> clone_x = x.clone()
>>> clone_x.stop_gradient = False
>>> z = clone_x**3
>>> z.backward()
>>> print(clone_x.stop_gradient)
False
>>> print(clone_x.grad)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False, 3.)
>>> print(x.stop_gradient)
True
>>> print(x.grad)
None

coalesce ( name: str | None = None ) → Tensor coalesce¶

the coalesced operator include sorted and merge, after coalesced, the indices of x is sorted and unique.

Parameters

x (Tensor) – the input SparseCooTensor.
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

return the SparseCooTensor after coalesced.

Return type

Tensor

Examples

>>> import paddle

>>> indices = [[0, 0, 1], [1, 1, 2]]
>>> values = [1.0, 2.0, 3.0]
>>> sp_x = paddle.sparse.sparse_coo_tensor(indices, values)
>>> sp_x = sp_x.coalesce()
>>> print(sp_x.indices())
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1],
[1, 2]])
>>> print(sp_x.values())
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[3., 3.])

cols ( ) cols¶

Note

This API is only available for SparseCsrTensor.

Returns the column index of non zero elements in input SparseCsrTensor.

Returns: DenseTensor

Examples

>>> import paddle

>>> crows = [0, 2, 3, 5]
>>> cols = [1, 3, 2, 0, 1]
>>> values = [1, 2, 3, 4, 5]
>>> dense_shape = [3, 4]
>>> csr = paddle.sparse.sparse_csr_tensor(crows, cols, values, dense_shape)
>>> csr.cols()
Tensor(shape=[5], dtype=int64, place=Place(gpu:0), stop_gradient=True,
[1, 3, 2, 0, 1])

combinations ( r: int = 2, with_replacement: bool = False, name: str | None = None ) → Tensor [source] combinations¶

Compute combinations of length r of the given tensor. The behavior is similar to python’s itertools.combinations when with_replacement is set to False, and itertools.combinations_with_replacement when with_replacement is set to True.

Parameters

x (Tensor) – 1-D input Tensor, the data type is float16, float32, float64, int32 or int64.
r (int, optional) – number of elements to combine, default value is 2.
with_replacement (bool, optional) – whether to allow duplication in combination, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to Name.

Returns

out (Tensor). Tensor concatenated by combinations, same dtype with x.

Examples

>>> import paddle
>>> x = paddle.to_tensor([1, 2, 3], dtype='int32')
>>> res = paddle.combinations(x)
>>> print(res)
Tensor(shape=[3, 2], dtype=int32, place=Place(gpu:0), stop_gradient=True,
       [[1, 2],
        [1, 3],
        [2, 3]])

concat ( axis: int | Tensor = 0, name: str | None = None ) → Tensor [source] concat¶

Concatenates the input along the axis. It doesn’t support 0-D Tensor because it requires a certain axis, and 0-D Tensor doesn’t have any axis.

The image illustrates a typical case of the concat operation. Two three-dimensional tensors with shapes [2, 3, 4] are concatenated along different axes, resulting in tensors of different shapes. The effects of concatenation along various dimensions are clearly visible.

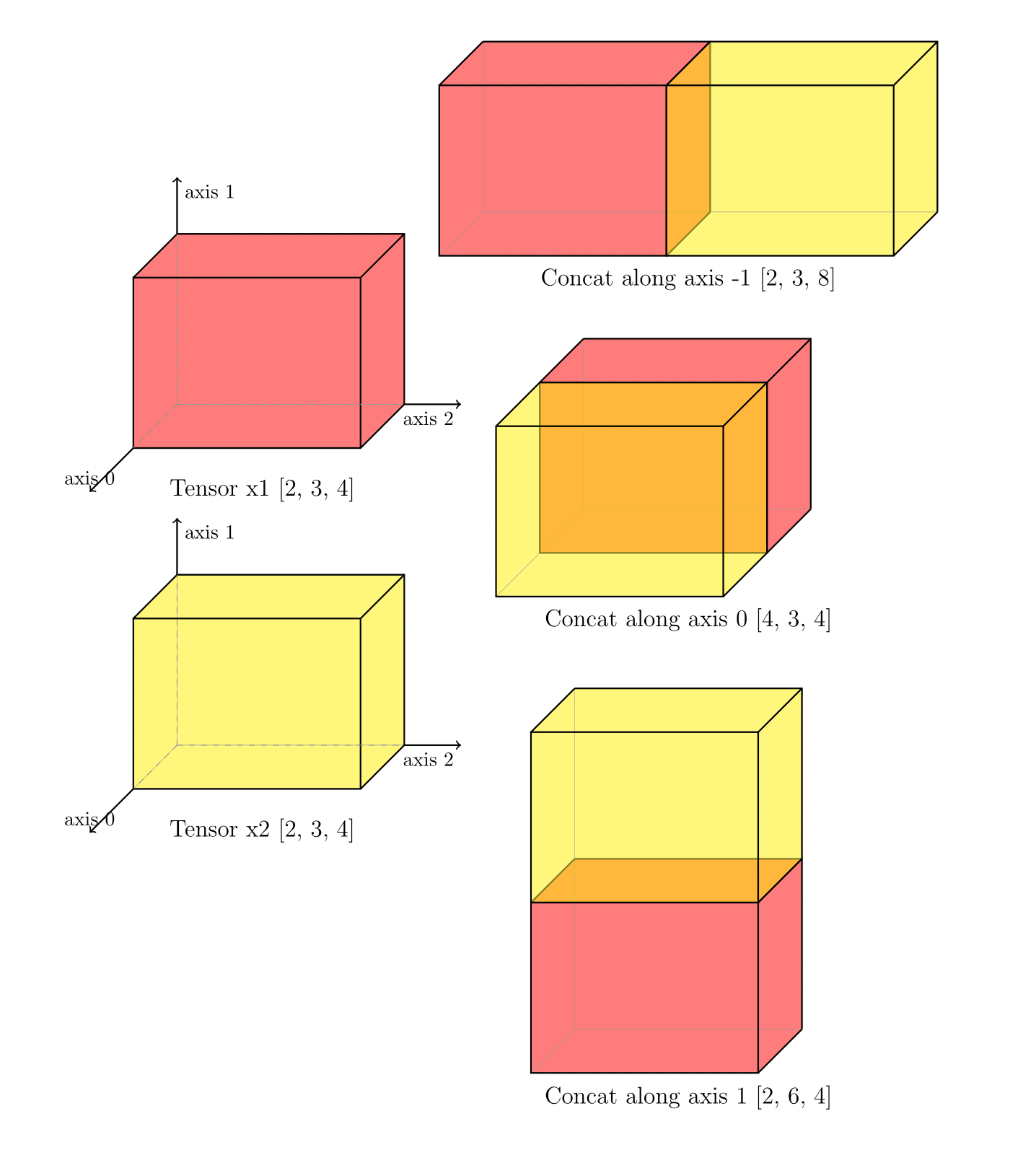
Parameters

x (list|tuple) – x is a Tensor list or Tensor tuple which is with data type bool, float16, bfloat16, float32, float64, int8, int16, int32, int64, uint8, uint16, complex64, complex128. All the Tensors in x must have same data type.
axis (int|Tensor, optional) – Specify the axis to operate on the input Tensors. Tt should be integer or 0-D int Tensor with shape []. The effective range is [-R, R), where R is Rank(x). When axis < 0, it works the same way as axis+R. Default is 0.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A Tensor with the same data type as x.

Examples

>>> import paddle

>>> x1 = paddle.to_tensor([[1, 2, 3],
...                        [4, 5, 6]])
>>> x2 = paddle.to_tensor([[11, 12, 13],
...                        [14, 15, 16]])
>>> x3 = paddle.to_tensor([[21, 22],
...                        [23, 24]])
>>> zero = paddle.full(shape=[1], dtype='int32', fill_value=0)
>>> # When the axis is negative, the real axis is (axis + Rank(x))
>>> # As follow, axis is -1, Rank(x) is 2, the real axis is 1
>>> out1 = paddle.concat(x=[x1, x2, x3], axis=-1)
>>> out2 = paddle.concat(x=[x1, x2], axis=0)
>>> out3 = paddle.concat(x=[x1, x2], axis=zero)
>>> print(out1)
Tensor(shape=[2, 8], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 , 11, 12, 13, 21, 22],
 [4 , 5 , 6 , 14, 15, 16, 23, 24]])
>>> print(out2)
Tensor(shape=[4, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 ],
 [4 , 5 , 6 ],
 [11, 12, 13],
 [14, 15, 16]])
>>> print(out3)
Tensor(shape=[4, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 ],
 [4 , 5 , 6 ],
 [11, 12, 13],
 [14, 15, 16]])

cond ( p: float | _POrder | None = None, name: str | None = None ) → Tensor cond¶

Computes the condition number of a matrix or batches of matrices with respect to a matrix norm p.

Parameters

x (Tensor) – The input tensor could be tensor of shape (*, m, n) where * is zero or more batch dimensions for p in (2, -2), or of shape (*, n, n) where every matrix is invertible for any supported p. And the input data type could be float32 or float64.
p (float|string, optional) – Order of the norm. Supported values are fro, nuc, 1, -1, 2, -2, inf, -inf. Default value is None, meaning that the order of the norm is 2.
name (str, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

computing results of condition number, its data type is the same as input Tensor x.

Return type

Tensor

Examples

>>> import paddle
>>> paddle.seed(2023)
>>> x = paddle.to_tensor([[1., 0, -1], [0, 1, 0], [1, 0, 1]])

>>> # compute conditional number when p is None
>>> out = paddle.linalg.cond(x)
>>> print(out)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
1.41421378)

>>> # compute conditional number when order of the norm is 'fro'
>>> out_fro = paddle.linalg.cond(x, p='fro')
>>> print(out_fro)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
3.16227770)

>>> # compute conditional number when order of the norm is 'nuc'
>>> out_nuc = paddle.linalg.cond(x, p='nuc')
>>> print(out_nuc)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
9.24264145)

>>> # compute conditional number when order of the norm is 1
>>> out_1 = paddle.linalg.cond(x, p=1)
>>> print(out_1)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
2.)

>>> # compute conditional number when order of the norm is -1
>>> out_minus_1 = paddle.linalg.cond(x, p=-1)
>>> print(out_minus_1)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
1.)

>>> # compute conditional number when order of the norm is 2
>>> out_2 = paddle.linalg.cond(x, p=2)
>>> print(out_2)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
1.41421378)

>>> # compute conditional number when order of the norm is -1
>>> out_minus_2 = paddle.linalg.cond(x, p=-2)
>>> print(out_minus_2)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
0.70710671)

>>> # compute conditional number when order of the norm is inf
>>> out_inf = paddle.linalg.cond(x, p=float("inf"))
>>> print(out_inf)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
2.)

>>> # compute conditional number when order of the norm is -inf
>>> out_minus_inf = paddle.linalg.cond(x, p=-float("inf"))
>>> print(out_minus_inf)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
1.)

>>> a = paddle.randn([2, 4, 4])
>>> print(a)
Tensor(shape=[2, 4, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[ 0.06132207,  1.11349595,  0.41906244, -0.24858207],
  [-1.85169315, -1.50370061,  1.73954511,  0.13331604],
  [ 1.66359663, -0.55764782, -0.59911072, -0.57773495],
  [-1.03176904, -0.33741450, -0.29695082, -1.50258386]],
 [[ 0.67233968, -1.07747352,  0.80170447, -0.06695852],
  [-1.85003340, -0.23008066,  0.65083790,  0.75387722],
  [ 0.61212337, -0.52664012,  0.19209868, -0.18707706],
  [-0.00711021,  0.35236868, -0.40404350,  1.28656745]]])

>>> a_cond_fro = paddle.linalg.cond(a, p='fro')
>>> print(a_cond_fro)
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[6.37173700 , 35.15114594])

>>> b = paddle.randn([2, 3, 4])
>>> print(b)
Tensor(shape=[2, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[ 0.03306439,  0.70149767,  0.77064633, -0.55978841],
  [-0.84461296,  0.99335045, -1.23486686,  0.59551388],
  [-0.63035583, -0.98797107,  0.09410731,  0.47007179]],
 [[ 0.85850012, -0.98949534, -1.63086998,  1.07340240],
  [-0.05492965,  1.04750168, -2.33754158,  1.16518629],
  [ 0.66847134, -1.05326962, -0.05703246, -0.48190674]]])

>>> b_cond_2 = paddle.linalg.cond(b, p=2)
>>> print(b_cond_2)
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[2.86566353, 6.85834455])

conj ( name: str | None = None ) → Tensor [source] conj¶

This function computes the conjugate of the Tensor elementwisely.

Parameters

x (Tensor) – The input Tensor which hold the complex numbers. Optional data types are: bfloat16, float16, complex64, complex128, float32, float64, int32 or int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The conjugate of input. The shape and data type is the same with input. If the elements of tensor is real type such as float32, float64, int32 or int64, the out is the same with input.

Return type

out (Tensor)

Examples

>>> import paddle

>>> data = paddle.to_tensor([[1+1j, 2+2j, 3+3j], [4+4j, 5+5j, 6+6j]])
>>> data
Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[(1+1j), (2+2j), (3+3j)],
 [(4+4j), (5+5j), (6+6j)]])

>>> conj_data = paddle.conj(data)
>>> conj_data
Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[(1-1j), (2-2j), (3-3j)],
 [(4-4j), (5-5j), (6-6j)]])

contiguous ( ) contiguous¶

Returns a contiguous in memory tensor containing the same data as current Tensor. If self tensor is already contiguous, this function returns the current Tensor.

Returns: Tensor, The contiguous Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = x[1]
>>> y = y.contiguous()
>>> print(y)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True, 2)

copysign ( y: Tensor | float, name: str | None = None ) → Tensor [source] copysign¶

Create a new floating-point tensor with the magnitude of input x and the sign of y, elementwise.

Equation:: \[\begin{split}copysign(x_{i},y_{i})=\left\{\begin{matrix} & -|x_{i}| & if \space y_{i} <= -0.0\\ & |x_{i}| & if \space y_{i} >= 0.0 \end{matrix}\right.\end{split}\]

Parameters

x (Tensor) – The input Tensor, magnitudes, the data type is bool, uint8, int8, int16, int32, int64, bfloat16, float16, float32, float64.
y (Tensor|float) – contains value(s) whose signbit(s) are applied to the magnitudes in input.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), the output tensor. The data type is the same as the input tensor.

Examples

>>> import paddle
>>> x = paddle.to_tensor([1, 2, 3], dtype='float64')
>>> y = paddle.to_tensor([-1, 1, -1], dtype='float64')
>>> out = paddle.copysign(x, y)
>>> print(out)
Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True,
       [-1.,  2., -3.])

>>> import paddle
>>> x = paddle.to_tensor([1, 2, 3], dtype='float64')
>>> y = paddle.to_tensor([-2], dtype='float64')
>>> res = paddle.copysign(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True,
       [-1.,  -2.,  -3.])

>>> import paddle
>>> x = paddle.to_tensor([1, 2, 3], dtype='float64')
>>> y = paddle.to_tensor([0.0], dtype='float64')
>>> out = paddle.copysign(x, y)
>>> print(out)
Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True,
    [1., 2., 3.])

>>> import paddle
>>> x = paddle.to_tensor([1, 2, 3], dtype='float64')
>>> y = paddle.to_tensor([-0.0], dtype='float64')
>>> out = paddle.copysign(x, y)
>>> print(out)
Tensor(shape=[3], dtype=float64, place=Place(gpu:0), stop_gradient=True,
    [-1., -2., -3.])

copysign_ ( y: Tensor, name: str | None = None ) → Tensor [source] copysign_¶: Inplace version of copysign API, the output Tensor will be inplaced with input x. Please refer to copysign.

corrcoef ( rowvar: bool = True, name: str | None = None ) → Tensor corrcoef¶

A correlation coefficient matrix indicate the correlation of each pair variables in the input matrix. For example, for an N-dimensional samples X=[x1,x2,…xN]T, then the correlation coefficient matrix element Rij is the correlation of xi and xj. The element Rii is the covariance of xi itself.

The relationship between the correlation coefficient matrix R and the covariance matrix C, is

\[R_{ij} = \frac{ C_{ij} } { \sqrt{ C_{ii} * C_{jj} } }\]

The values of R are between -1 and 1.

Parameters

x (Tensor) – A N-D(N<=2) Tensor containing multiple variables and observations. By default, each row of x represents a variable. Also see rowvar below.
rowvar (bool, optional) – If rowvar is True (default), then each row represents a variable, with observations in the columns. Default: True.
name (str|None, optional) – Name of the output. It’s used to print debug info for developers. Details: Name. Default: None.

Returns

The correlation coefficient matrix of the variables.

Examples

>>> import paddle
>>> paddle.seed(2023)

>>> xt = paddle.rand((3,4))
>>> print(paddle.linalg.corrcoef(xt))
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 0.99999988, -0.47689581, -0.89559376],
 [-0.47689593,  1.        ,  0.16345492],
 [-0.89559382,  0.16345496,  1.        ]])

cos ( name: str | None = None ) → Tensor [source] cos¶

Cosine Operator. Computes cosine of x element-wise.

Input range is (-inf, inf) and output range is [-1,1].

\[out = cos(x)\]

Parameters

x (Tensor) – Input of Cos operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Cos operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.cos(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.92106098, 0.98006660, 0.99500418, 0.95533651])

cos_ ( name=None ) cos_¶: Inplace version of cos API, the output Tensor will be inplaced with input x. Please refer to cos.

cosh ( name: str | None = None ) → Tensor [source] cosh¶

Cosh Activation Operator.

Input range (-inf, inf), output range (1, inf).

\[out = \frac{exp(x)+exp(-x)}{2}\]

Parameters

x (Tensor) – Input of Cosh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Cosh operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.cosh(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.08107233, 1.02006674, 1.00500417, 1.04533851])

cosh_ ( name=None ) cosh_¶: Inplace version of cosh API, the output Tensor will be inplaced with input x. Please refer to cosh.

count_nonzero ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] count_nonzero¶

Counts the number of non-zero values in the tensor x along the specified axis.

Parameters

x (Tensor) – An N-D Tensor, the data type is bool, float16, float32, float64, int32 or int64.
axis (int|list|tuple, optional) – The dimensions along which the sum is performed. If None, sum all elements of x and return a Tensor with a single element, otherwise must be in the range $[-rank(x), rank(x))$. If $axis[i] < 0$, the dimension to reduce is $rank + axis[i]$.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Results of count operation on the specified axis of input Tensor x, it’s data type is ‘int64’.

Return type

Tensor

Examples

>>> import paddle
>>> # x is a 2-D Tensor:
>>> x = paddle.to_tensor([[0., 1.1, 1.2], [0., 0., 1.3], [0., 0., 0.]])
>>> out1 = paddle.count_nonzero(x)
>>> out1
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
3)
>>> out2 = paddle.count_nonzero(x, axis=0)
>>> out2
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 1, 2])
>>> out3 = paddle.count_nonzero(x, axis=0, keepdim=True)
>>> out3
Tensor(shape=[1, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1, 2]])
>>> out4 = paddle.count_nonzero(x, axis=1)
>>> out4
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[2, 1, 0])
>>> out5 = paddle.count_nonzero(x, axis=1, keepdim=True)
>>> out5
Tensor(shape=[3, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[2],
 [1],
 [0]])

>>> # y is a 3-D Tensor:
>>> y = paddle.to_tensor([[[0., 1.1, 1.2], [0., 0., 1.3], [0., 0., 0.]],
...                         [[0., 2.5, 2.6], [0., 0., 2.4], [2.1, 2.2, 2.3]]])
>>> out6 = paddle.count_nonzero(y, axis=[1, 2])
>>> out6
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[3, 6])
>>> out7 = paddle.count_nonzero(y, axis=[0, 1])
>>> out7
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 3, 5])

cov ( rowvar: bool = True, ddof: bool = True, fweights: Tensor | None = None, aweights: Tensor | None = None, name: str | None = None ) → Tensor cov¶

Estimate the covariance matrix of the input variables, given data and weights.

A covariance matrix is a square matrix, indicate the covariance of each pair variables in the input matrix. For example, for an N-dimensional samples X=[x1,x2,…xN]T, then the covariance matrix element Cij is the covariance of xi and xj. The element Cii is the variance of xi itself.

Parameters

x (Tensor) – A N-D(N<=2) Tensor containing multiple variables and observations. By default, each row of x represents a variable. Also see rowvar below.
rowvar (bool, optional) – If rowvar is True (default), then each row represents a variable, with observations in the columns. Default: True.
ddof (bool, optional) – If ddof=True will return the unbiased estimate, and ddof=False will return the simple average. Default: True.
fweights (Tensor, optional) – 1-D Tensor of integer frequency weights; The number of times each observation vector should be repeated. Default: None.
aweights (Tensor, optional) – 1-D Tensor of observation vector weights. How important of the observation vector, larger data means this element is more important. Default: None.
name (str|None, optional) – Name of the output. Default is None. It’s used to print debug info for developers. Details: Name .

Returns

The covariance matrix Tensor of the variables.

Return type

Tensor

Examples

>>> import paddle
>>> paddle.seed(2023)

>>> xt = paddle.rand((3, 4))
>>> paddle.linalg.cov(xt)
>>> print(xt)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.86583614, 0.52014720, 0.25960937, 0.90525323],
 [0.42400089, 0.40641287, 0.97020894, 0.74437362],
 [0.51785129, 0.73292869, 0.97786582, 0.04315904]])

create_parameter ( dtype: DTypeLike, name: str | None = None, attr: ParamAttrLike | None = None, is_bias: bool = False, default_initializer: paddle.nn.initializer.Initializer | None = None ) → paddle.Tensor [source] create_parameter¶

This function creates a parameter. The parameter is a learnable variable, which can have gradient, and can be optimized.

Note

This is a very low-level API. This API is useful when you create operator by your self, instead of using layers.

Parameters

shape (list of int) – Shape of the parameter
dtype (str) – Data type of the parameter. It can be set as ‘float16’, ‘float32’, ‘float64’.
name (str|None, optional) – For detailed information, please refer to Name . Usually name is no need to set and None by default.
attr (ParamAttr|None, optional) – Attribute object of the specified argument. For detailed information, please refer to ParamAttr None by default, which means that ParamAttr will be initialized as it is.
is_bias (bool, optional) – This can affect which default initializer is chosen when default_initializer is None. If is_bias, initializer.Constant(0.0) will be used. Otherwise, Xavier() will be used.
default_initializer (Initializer|None, optional) – Initializer for the parameter

Returns

The created parameter.

Examples

>>> import paddle
>>> paddle.enable_static()
>>> W = paddle.create_parameter(shape=[784, 200], dtype='float32')

create_tensor ( name: str | None = None, persistable: bool = False ) → paddle.Tensor create_tensor¶

Create a variable, which will hold a Tensor with data type dtype.

Parameters

dtype (string|numpy.dtype) – the data type of Tensor to be created, the data type is bool, float16, float32, float64, int8, int16, int32 and int64.
name (string, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name
persistable (bool) – Set the persistable flag of the create tensor. default value is False.

Returns

The tensor to be created according to dtype.

Return type

Variable

Examples

>>> import paddle
>>> tensor = paddle.tensor.create_tensor(dtype='float32')

cross ( y: Tensor, axis: int = 9, name: str | None = None ) → Tensor [source] cross¶

Computes the cross product between two tensors along an axis.

Inputs must have the same shape, and the length of their axes should be equal to 3. If axis is not given, it defaults to the first axis found with the length 3.

Parameters

x (Tensor) – The first input tensor, the data type is float16, float32, float64, int32, int64, complex64, complex128.
y (Tensor) – The second input tensor, the data type is float16, float32, float64, int32, int64, complex64, complex128.
axis (int, optional) – The axis along which to compute the cross product. It defaults to be 9 which indicates using the first axis found with the length 3.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. A Tensor with same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 1.0, 1.0],
...                         [2.0, 2.0, 2.0],
...                         [3.0, 3.0, 3.0]])
>>> y = paddle.to_tensor([[1.0, 1.0, 1.0],
...                         [1.0, 1.0, 1.0],
...                         [1.0, 1.0, 1.0]])
...
>>> z1 = paddle.cross(x, y)
>>> print(z1)
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[-1., -1., -1.],
 [ 2.,  2.,  2.],
 [-1., -1., -1.]])

>>> z2 = paddle.cross(x, y, axis=1)
>>> print(z2)
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 0., 0.],
 [0., 0., 0.],
 [0., 0., 0.]])

crows ( ) crows¶

Note

This API is only available for SparseCsrTensor.

Returns the compressed row index of non zero elements in input SparseCsrTensor.

Returns: DenseTensor

Examples

>>> import paddle

>>> crows = [0, 2, 3, 5]
>>> cols = [1, 3, 2, 0, 1]
>>> values = [1, 2, 3, 4, 5]
>>> dense_shape = [3, 4]
>>> csr = paddle.sparse.sparse_csr_tensor(crows, cols, values, dense_shape)
>>> csr.crows()
Tensor(shape=[4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
[0, 2, 3, 5])

cummax ( axis: int | None = None, dtype: DTypeLike = 'int64', name: str | None = None ) → tuple[Tensor, Tensor] [source] cummax¶

The cumulative max of the elements along a given axis.

Note

The first element of the result is the same as the first element of the input.

Parameters

x (Tensor) – The input tensor needed to be cummaxed.
axis (int, optional) – The dimension to accumulate along. -1 means the last dimension. The default (None) is to compute the cummax over the flattened array.
dtype (str|paddle.dtype|np.dtype, optional) – The data type of the indices tensor, can be int32, int64. The default value is int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), The result of cummax operation. The dtype of cummax result is same with input x.

indices (Tensor), The corresponding index results of cummax operation.

Examples

>>> import paddle

>>> data = paddle.to_tensor([-1, 5, 0, -2, -3, 2])
>>> data = paddle.reshape(data, (2, 3))

>>> value, indices = paddle.cummax(data)
>>> value
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[-1,  5,  5,  5,  5,  5])
>>> indices
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 1, 1, 1, 1, 1])

>>> value, indices = paddle.cummax(data, axis=0)
>>> value
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[-1,  5,  0],
 [-1,  5,  2]])
>>> indices
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 0],
 [0, 0, 1]])

>>> value, indices = paddle.cummax(data, axis=-1)
>>> value
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[-1,  5,  5],
 [-2, -2,  2]])
>>> indices
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1, 1],
 [0, 0, 2]])

>>> value, indices = paddle.cummax(data, dtype='int64')
>>> assert indices.dtype == paddle.int64

cummin ( axis: int | None = None, dtype: DTypeLike = 'int64', name: str | None = None ) → tuple[Tensor, Tensor] [source] cummin¶

The cumulative min of the elements along a given axis.

Note

The first element of the result is the same as the first element of the input.

Parameters

x (Tensor) – The input tensor needed to be cummined.
axis (int, optional) – The dimension to accumulate along. -1 means the last dimension. The default (None) is to compute the cummin over the flattened array.
dtype (str|paddle.dtype|np.dtype, optional) – The data type of the indices tensor, can be int32, int64. The default value is int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), The result of cummin operation. The dtype of cummin result is same with input x.

indices (Tensor), The corresponding index results of cummin operation.

Examples

>>> import paddle
>>> data = paddle.to_tensor([-1, 5, 0, -2, -3, 2])
>>> data = paddle.reshape(data, (2, 3))

>>> value, indices = paddle.cummin(data)
>>> value
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[-1, -1, -1, -2, -3, -3])
>>> indices
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 0, 0, 3, 4, 4])

>>> value, indices = paddle.cummin(data, axis=0)
>>> value
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[-1,  5,  0],
 [-2, -3,  0]])
>>> indices
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 0],
 [1, 1, 0]])

>>> value, indices = paddle.cummin(data, axis=-1)
>>> value
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[-1, -1, -1],
 [-2, -3, -3]])
>>> indices
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 0],
 [0, 1, 1]])

>>> value, indices = paddle.cummin(data, dtype='int64')
>>> assert indices.dtype == paddle.int64

cumprod ( dim: int | None = None, dtype: DTypeLike | None = None, name: str | None = None ) → Tensor [source] cumprod¶

Compute the cumulative product of the input tensor x along a given dimension dim.

Note

The first element of the result is the same as the first element of the input.

Parameters

x (Tensor) – the input tensor need to be cumproded.
dim (int|None, optional) – the dimension along which the input tensor will be accumulated. It need to be in the range of [-x.rank, x.rank), where x.rank means the dimensions of the input tensor x and -1 means the last dimension.
dtype (str|paddle.dtype|np.dtype, optional) – The data type of the output tensor, can be bfloat16, float16, float32, float64, int32, int64, complex64, complex128. If specified, the input tensor is casted to dtype before the operation is performed. This is useful for preventing data type overflows. The default value is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the result of cumprod operator.

Examples

>>> import paddle

>>> data = paddle.arange(12)
>>> data = paddle.reshape(data, (3, 4))
>>> data
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0 , 1 , 2 , 3 ],
 [4 , 5 , 6 , 7 ],
 [8 , 9 , 10, 11]])

>>> y = paddle.cumprod(data, dim=0)
>>> y
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0  , 1  , 2  , 3  ],
 [0  , 5  , 12 , 21 ],
 [0  , 45 , 120, 231]])

>>> y = paddle.cumprod(data, dim=-1)
>>> y
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0   , 0   , 0   , 0   ],
 [4   , 20  , 120 , 840 ],
 [8   , 72  , 720 , 7920]])

>>> y = paddle.cumprod(data, dim=1, dtype='float64')
>>> y
Tensor(shape=[3, 4], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0.   , 0.   , 0.   , 0.   ],
 [4.   , 20.  , 120. , 840. ],
 [8.   , 72.  , 720. , 7920.]])

>>> assert y.dtype == paddle.float64

cumprod_ ( dim: int | None = None, dtype: DTypeLike | None = None, name: str | None = None ) → Tensor [source] cumprod_¶: Inplace version of cumprod API, the output Tensor will be inplaced with input x. Please refer to cumprod.

cumsum ( axis: int | None = None, dtype: DTypeLike | None = None, name: str | None = None ) → Tensor [source] cumsum¶

The cumulative sum of the elements along a given axis.

Note

The first element of the result is the same as the first element of the input.

Parameters

x (Tensor) – The input tensor needed to be cumsumed.
axis (int, optional) – The dimension to accumulate along. -1 means the last dimension. The default (None) is to compute the cumsum over the flattened array.
dtype (str|paddle.dtype|np.dtype|None, optional) – The data type of the output tensor, can be bfloat16, float16, float32, float64, int32, int64, complex64, complex128. If specified, the input tensor is casted to dtype before the operation is performed. This is useful for preventing data type overflows. The default value is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the result of cumsum operator.

Examples

>>> import paddle

>>> data = paddle.arange(12)
>>> data = paddle.reshape(data, (3, 4))

>>> y = paddle.cumsum(data)
>>> y
Tensor(shape=[12], dtype=int64, place=Place(cpu), stop_gradient=True,
[0 , 1 , 3 , 6 , 10, 15, 21, 28, 36, 45, 55, 66])

>>> y = paddle.cumsum(data, axis=0)
>>> y
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0 , 1 , 2 , 3 ],
 [4 , 6 , 8 , 10],
 [12, 15, 18, 21]])

>>> y = paddle.cumsum(data, axis=-1)
>>> y
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0 , 1 , 3 , 6 ],
 [4 , 9 , 15, 22],
 [8 , 17, 27, 38]])

>>> y = paddle.cumsum(data, dtype='float64')
>>> assert y.dtype == paddle.float64

cumsum_ ( axis: int | None = None, dtype: DTypeLike | None = None, name: str | None = None ) → Tensor [source] cumsum_¶: Inplace version of cumprod API, the output Tensor will be inplaced with input x. Please refer to cumprod.

cumulative_trapezoid ( x: Tensor | None = None, dx: float | None = None, axis: int = -1, name: str | None = None ) → Tensor [source] cumulative_trapezoid¶

Integrate along the given axis using the composite trapezoidal rule. Use the cumsum method

Parameters

y (Tensor) – Input tensor to integrate. It’s data type should be float16, float32, float64.
x (Tensor|None, optional) – The sample points corresponding to the y values, the same type as y. It is known that the size of y is [d_1, d_2, … , d_n] and $axis=k$, then the size of x can only be [d_k] or [d_1, d_2, … , d_n ]. If x is None, the sample points are assumed to be evenly spaced dx apart. The default is None.
dx (float|None, optional) – The spacing between sample points when x is None. If neither x nor dx is provided then the default is $dx = 1$.
axis (int, optional) – The axis along which to integrate. The default is -1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Definite integral of y is N-D tensor as approximated along a single axis by the trapezoidal rule. The result is an N-D tensor.

Examples

>>> import paddle

>>> y = paddle.to_tensor([4, 5, 6], dtype='float32')

>>> paddle.cumulative_trapezoid(y)
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[4.50000000, 10.       ])

>>> paddle.cumulative_trapezoid(y, dx=2.)
>>> # Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
>>> #        [9. , 20.])

>>> y = paddle.to_tensor([4, 5, 6], dtype='float32')
>>> x = paddle.to_tensor([1, 2, 3], dtype='float32')

>>> paddle.cumulative_trapezoid(y, x)
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[4.50000000, 10.       ])

>>> y = paddle.to_tensor([1, 2, 3], dtype='float64')
>>> x = paddle.to_tensor([8, 6, 4], dtype='float64')

>>> paddle.cumulative_trapezoid(y, x)
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=True,
[-3., -8.])

>>> y = paddle.arange(6).reshape((2, 3)).astype('float32')

>>> paddle.cumulative_trapezoid(y, axis=0)
Tensor(shape=[1, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.50000000, 2.50000000, 3.50000000]])
>>> paddle.cumulative_trapezoid(y, axis=1)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.50000000, 2.        ],
 [3.50000000, 8.        ]])

data

Tensor’s self.

Returns: self.
Return type: Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.)
>>> print(x)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
1.)

>>> print(x.data)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
1.)

>>> x.data = paddle.to_tensor(2.)
>>> print(x)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
2.)

>>> print(x.data)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
2.)

data_ptr ( ) data_ptr¶

Returns the address of the first element of current Tensor.

Returns: int, The address of the first element of current Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> print(x.data_ptr())
>>> 
93220864
>>> 

deg2rad ( name: str | None = None ) → Tensor [source] deg2rad¶

Convert each of the elements of input x from degrees to angles in radians.

\[deg2rad(x)=\pi * x / 180\]

Parameters

x (Tensor) – An N-D Tensor, the data type is float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor, the shape and data type is the same with input (The output data type is float32 when the input data type is int).

Return type

out (Tensor)

Examples

>>> import paddle

>>> x1 = paddle.to_tensor([180.0, -180.0, 360.0, -360.0, 90.0, -90.0])
>>> result1 = paddle.deg2rad(x1)
>>> result1
Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True,
[3.14159274, -3.14159274,  6.28318548, -6.28318548,  1.57079637,
-1.57079637])

>>> x2 = paddle.to_tensor(180)
>>> result2 = paddle.deg2rad(x2)
>>> result2
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
3.14159274)

dense_dim ( ) dense_dim¶

Returns the number of dense dimensions of sparse Tensor.

Note

If self is not sparse Tensor, return len(self.shape).

Returns: int, dense dim of self Tensor

Examples

>>> import paddle
>>> import numpy as np

>>> indices = [[0, 1, 1], [2, 0, 2]]
>>> values = np.array([[3, 4], [5, 6], [7, 8]])
>>> dense_shape = [2, 3, 2]
>>> coo = paddle.sparse.sparse_coo_tensor(indices, values, dense_shape)
>>> coo.dense_dim()
1

>>> crows = [0, 2, 3, 5]
>>> cols = [1, 3, 2, 0, 1]
>>> values = [1, 2, 3, 4, 5]
>>> dense_shape = [3, 4]
>>> csr = paddle.sparse.sparse_csr_tensor(crows, cols, values, dense_shape)
>>> csr.dense_dim()
0

>>> dense = paddle.to_tensor([[1, 2, 3]])
>>> dense.dense_dim()
>>> 2

detach ( ) detach¶

Returns a new Tensor, detached from the current graph. It will share data with origin Tensor and always doesn’t have a Tensor copy. In addition, the detached Tensor doesn’t provide gradient propagation.

Returns: Tensor, The detached Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1.0], stop_gradient=False)
>>> detach_x = x.detach()
>>> detach_x[0] = 10.0
>>> print(x)
Tensor(shape=[1], dtype=float32, place=CPUPlace, stop_gradient=False, [10.])

>>> y = x**2
>>> y.backward()
>>> print(x.grad)
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=False, [20.])

>>> print(detach_x.grad) # None, 'stop_gradient=True' by default
None

>>> detach_x.stop_gradient = False # Set stop_gradient to be False, supported auto-grad
>>> z = detach_x**3
>>> z.backward()

>>> print(x.grad)
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=False, [20.])

>>> print(detach_x.grad)
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=False, [300.])

>>> # Due to sharing of data with origin Tensor, There are some unsafe operations:
>>> # y = 2 * x
>>> # detach_x[:] = 5.0
>>> # y.backward()
>>> # It will raise Error:
>>> #   one of the variables needed for gradient computation has been modified by an inplace operation.

detach_ ( ) detach_¶

Detach self from the current graph, and returns self Tensor. In addition, the detached Tensor doesn’t provide gradient propagation.

Returns: Tensor, The detached Tensor.

diag ( offset: int = 0, padding_value: int = 0, name: Optional[str] = None ) → Tensor [source] diag¶

If x is a vector (1-D tensor), a 2-D square tensor with the elements of x as the diagonal is returned.

If x is a matrix (2-D tensor), a 1-D tensor with the diagonal elements of x is returned.

The argument offset controls the diagonal offset:

If offset = 0, it is the main diagonal.

If offset > 0, it is superdiagonal.

If offset < 0, it is subdiagonal.

Parameters

x (Tensor) – The input tensor. Its shape is either 1-D or 2-D. Its data type should be float16, float32, float64, int32, int64, complex64, complex128.
offset (int, optional) – The diagonal offset. A positive value represents superdiagonal, 0 represents the main diagonal, and a negative value represents subdiagonal.
padding_value (int|float, optional) – Use this value to fill the area outside the specified diagonal band. Only takes effect when the input is a 1-D Tensor. The default value is 0.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, a square matrix or a vector. The output data type is the same as input data type.

Examples

>>> import paddle

>>> paddle.disable_static()
>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.diag(x)
>>> print(y)
Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 0, 0],
 [0, 2, 0],
 [0, 0, 3]])

>>> y = paddle.diag(x, offset=1)
>>> print(y)
Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1, 0, 0],
 [0, 0, 2, 0],
 [0, 0, 0, 3],
 [0, 0, 0, 0]])

>>> y = paddle.diag(x, padding_value=6)
>>> print(y)
Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 6, 6],
 [6, 2, 6],
 [6, 6, 3]])

>>> import paddle

>>> paddle.disable_static()
>>> x = paddle.to_tensor([[1, 2, 3], [4, 5, 6]])
>>> y = paddle.diag(x)
>>> print(y)
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 5])

>>> y = paddle.diag(x, offset=1)
>>> print(y)
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[2, 6])

>>> y = paddle.diag(x, offset=-1)
>>> print(y)
Tensor(shape=[1], dtype=int64, place=Place(cpu), stop_gradient=True,
[4])

diag_embed ( offset: int = 0, dim1: int = -2, dim2: int = -1 ) → paddle.Tensor [source] diag_embed¶

Creates a tensor whose diagonals of certain 2D planes (specified by dim1 and dim2) are filled by input. By default, a 2D plane formed by the last two dimensions of the returned tensor will be selected.

The argument offset determines which diagonal is generated:

If offset = 0, it is the main diagonal.
If offset > 0, it is above the main diagonal.
If offset < 0, it is below the main diagonal.

Parameters

input (Tensor|numpy.ndarray) – The input tensor. Must be at least 1-dimensional. The input data type should be float32, float64, int32, int64.
offset (int, optional) – Which diagonal to consider. Default: 0 (main diagonal).
dim1 (int, optional) – The first dimension with respect to which to take diagonal. Default: -2.
dim2 (int, optional) – The second dimension with respect to which to take diagonal. Default: -1.

Returns

Tensor, the output data type is the same as input data type.

Examples

>>> import paddle

>>> diag_embed_input = paddle.arange(6)

>>> diag_embed_output1 = paddle.diag_embed(diag_embed_input)
>>> print(diag_embed_output1)
Tensor(shape=[6, 6], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 0, 0, 0, 0],
 [0, 1, 0, 0, 0, 0],
 [0, 0, 2, 0, 0, 0],
 [0, 0, 0, 3, 0, 0],
 [0, 0, 0, 0, 4, 0],
 [0, 0, 0, 0, 0, 5]])

>>> diag_embed_output2 = paddle.diag_embed(diag_embed_input, offset=-1, dim1=0,dim2=1 )
>>> print(diag_embed_output2)
Tensor(shape=[7, 7], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0, 0, 0],
 [0, 1, 0, 0, 0, 0, 0],
 [0, 0, 2, 0, 0, 0, 0],
 [0, 0, 0, 3, 0, 0, 0],
 [0, 0, 0, 0, 4, 0, 0],
 [0, 0, 0, 0, 0, 5, 0]])

>>> diag_embed_input_2dim = paddle.reshape(diag_embed_input,[2,3])
>>> print(diag_embed_input_2dim)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1, 2],
[3, 4, 5]])
>>> diag_embed_output3 = paddle.diag_embed(diag_embed_input_2dim,offset= 0, dim1=0, dim2=2 )
>>> print(diag_embed_output3)
Tensor(shape=[3, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[0, 0, 0],
  [3, 0, 0]],
 [[0, 1, 0],
  [0, 4, 0]],
 [[0, 0, 2],
  [0, 0, 5]]])

diagflat ( offset: int = 0, name: Optional[str] = None ) → Tensor [source] diagflat¶

If x is a vector (1-D tensor), a 2-D square tensor with the elements of x as the diagonal is returned.

If x is a tensor (more than 1-D), a 2-D square tensor with the elements of flattened x as the diagonal is returned.

The argument offset controls the diagonal offset.

If offset = 0, it is the main diagonal.

If offset > 0, it is superdiagonal.

If offset < 0, it is subdiagonal.

Parameters

x (Tensor) – The input tensor. It can be any shape. Its data type should be float16, float32, float64, int32, int64.
offset (int, optional) – The diagonal offset. A positive value represents superdiagonal, 0 represents the main diagonal, and a negative value represents subdiagonal. Default: 0 (main diagonal).
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, a square matrix. The output data type is the same as input data type.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.diagflat(x)
>>> print(y)
Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 0, 0],
 [0, 2, 0],
 [0, 0, 3]])

>>> y = paddle.diagflat(x, offset=1)
>>> print(y)
Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1, 0, 0],
 [0, 0, 2, 0],
 [0, 0, 0, 3],
 [0, 0, 0, 0]])

>>> y = paddle.diagflat(x, offset=-1)
>>> print(y)
Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 0, 0],
 [1, 0, 0, 0],
 [0, 2, 0, 0],
 [0, 0, 3, 0]])

>>> import paddle

>>> x = paddle.to_tensor([[1, 2], [3, 4]])
>>> y = paddle.diagflat(x)
>>> print(y)
Tensor(shape=[4, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 0, 0, 0],
 [0, 2, 0, 0],
 [0, 0, 3, 0],
 [0, 0, 0, 4]])

>>> y = paddle.diagflat(x, offset=1)
>>> print(y)
Tensor(shape=[5, 5], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1, 0, 0, 0],
 [0, 0, 2, 0, 0],
 [0, 0, 0, 3, 0],
 [0, 0, 0, 0, 4],
 [0, 0, 0, 0, 0]])

>>> y = paddle.diagflat(x, offset=-1)
>>> print(y)
Tensor(shape=[5, 5], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 0, 0, 0],
 [1, 0, 0, 0, 0],
 [0, 2, 0, 0, 0],
 [0, 0, 3, 0, 0],
 [0, 0, 0, 4, 0]])

diagonal ( offset: int = 0, axis1: int = 0, axis2: int = 1, name: str | None = None ) → Tensor [source] diagonal¶

Computes the diagonals of the input tensor x.

If x is 2D, returns the diagonal. If x has larger dimensions, diagonals be taken from the 2D planes specified by axis1 and axis2. By default, the 2D planes formed by the first and second axis of the input tensor x.

The argument offset determines where diagonals are taken from input tensor x:

If offset = 0, it is the main diagonal.
If offset > 0, it is above the main diagonal.
If offset < 0, it is below the main diagonal.

Parameters

x (Tensor) – The input tensor x. Must be at least 2-dimensional. The input data type should be bool, int32, int64, bfloat16, float16, float32, float64.
offset (int, optional) – Which diagonals in input tensor x will be taken. Default: 0 (main diagonals).
axis1 (int, optional) – The first axis with respect to take diagonal. Default: 0.
axis2 (int, optional) – The second axis with respect to take diagonal. Default: 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

a partial view of input tensor in specify two dimensions, the output data type is the same as input data type.

Return type

Tensor

Examples

>>> import paddle

>>> paddle.seed(2023)
>>> x = paddle.rand([2, 2, 3],'float32')
>>> print(x)
Tensor(shape=[2, 2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[0.86583614, 0.52014720, 0.25960937],
  [0.90525323, 0.42400089, 0.40641287]],
 [[0.97020894, 0.74437362, 0.51785129],
  [0.73292869, 0.97786582, 0.04315904]]])

>>> out1 = paddle.diagonal(x)
>>> print(out1)
Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.86583614, 0.73292869],
 [0.52014720, 0.97786582],
 [0.25960937, 0.04315904]])

>>> out2 = paddle.diagonal(x, offset=0, axis1=2, axis2=1)
>>> print(out2)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.86583614, 0.42400089],
 [0.97020894, 0.97786582]])

>>> out3 = paddle.diagonal(x, offset=1, axis1=0, axis2=1)
>>> print(out3)
Tensor(shape=[3, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.90525323],
 [0.42400089],
 [0.40641287]])

>>> out4 = paddle.diagonal(x, offset=0, axis1=1, axis2=2)
>>> print(out4)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.86583614, 0.42400089],
 [0.97020894, 0.97786582]])

diagonal_scatter ( y: Tensor, offset: int = 0, axis1: int = 0, axis2: int = 1, name: str | None = None ) → Tensor [source] diagonal_scatter¶

Embed the values of Tensor y into Tensor x along the diagonal elements of Tensor x, with respect to axis1 and axis2.

This function returns a tensor with fresh storage.

The argument offset controls which diagonal to consider:

If offset = 0, it is the main diagonal.
If offset > 0, it is above the main diagonal.
If offset < 0, it is below the main diagonal.

Note

y should have the same shape as paddle.diagonal.

The image below demonstrates the example: A 2D tensor with a shape of [2, 3] is diagonal_scatter along its main diagonal (offset = 0) within axis1 = 0 and axis2 = 1 using a 1D tensor filled with ones.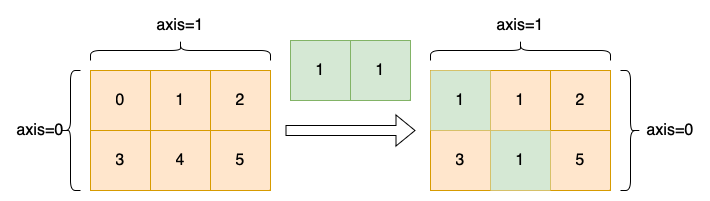

Parameters

x (Tensor) – x is the original Tensor. Must be at least 2-dimensional.
y (Tensor) – y is the Tensor to embed into x
offset (int, optional) – which diagonal to consider. Default: 0 (main diagonal).
axis1 (int, optional) – first axis with respect to which to take diagonal. Default: 0.
axis2 (int, optional) – second axis with respect to which to take diagonal. Default: 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Tensor with diagonal embedded with y.

Examples

>>> import paddle
>>> x = paddle.arange(6.0).reshape((2, 3))
>>> y = paddle.ones((2,))
>>> out = x.diagonal_scatter(y)
>>> print(out)
Tensor(shape=[2, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[1., 1., 2.],
        [3., 1., 5.]])

diff ( n: int = 1, axis: int = -1, prepend: Tensor | None = None, append: Tensor | None = None, name: str | None = None ) → Tensor [source] diff¶

Computes the n-th forward difference along the given axis. The first-order differences is computed by using the following formula:

\[out[i] = x[i+1] - x[i]\]

Higher-order differences are computed by using paddle.diff() recursively. The number of n supports any positive integer value.

Parameters

x (Tensor) – The input tensor to compute the forward difference on, the data type is float16, float32, float64, bool, int32, int64.
n (int, optional) – The number of times to recursively compute the difference. Supports any positive integer value. Default:1
axis (int, optional) – The axis to compute the difference along. Default:-1
prepend (Tensor|None, optional) – The tensor to prepend to input along axis before computing the difference. It’s dimensions must be equivalent to that of x, and its shapes must match x’s shape except on axis.
append (Tensor|None, optional) – The tensor to append to input along axis before computing the difference, It’s dimensions must be equivalent to that of x, and its shapes must match x’s shape except on axis.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output tensor with same dtype with x.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 4, 5, 2])
>>> out = paddle.diff(x)
>>> out
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[ 3,  1, -3])

>>> x_2 = paddle.to_tensor([1, 4, 5, 2])
>>> out = paddle.diff(x_2, n=2)
>>> out
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[ -2,  -4])

>>> y = paddle.to_tensor([7, 9])
>>> out = paddle.diff(x, append=y)
>>> out
Tensor(shape=[5], dtype=int64, place=Place(cpu), stop_gradient=True,
[ 3,  1, -3,  5,  2])

>>> out = paddle.diff(x, n=2, append=y)
>>> out
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[-2, -4,  8, -3])

>>> out = paddle.diff(x, n=3, append=y)
>>> out
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[-2 ,  12, -11])

>>> z = paddle.to_tensor([[1, 2, 3], [4, 5, 6]])
>>> out = paddle.diff(z, axis=0)
>>> out
Tensor(shape=[1, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 3, 3]])
>>> out = paddle.diff(z, axis=1)
>>> out
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 1],
 [1, 1]])

digamma ( name: str | None = None ) → Tensor [source] digamma¶

Calculates the digamma of the given input tensor, element-wise.

\[Out = \Psi(x) = \frac{ \Gamma^{'}(x) }{ \Gamma(x) }\]

Parameters

x (Tensor) – Input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the digamma of the input Tensor, the shape and data type is the same with input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> data = paddle.to_tensor([[1, 1.5], [0, -2.2]], dtype='float32')
>>> res = paddle.digamma(data)
>>> res
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[-0.57721591,  0.03648996],
 [ nan       ,  5.32286835]])

digamma_ ( name: str | None = None ) → Tensor [source] digamma_¶: Inplace version of digamma API, the output Tensor will be inplaced with input x. Please refer to digamma.

dist ( y: Tensor, p: float = 2, name: str | None = None ) → Tensor [source] dist¶

Returns the p-norm of (x - y). It is not a norm in a strict sense, only as a measure of distance. The shapes of x and y must be broadcastable. The definition is as follows, for details, please refer to the Introduction to Tensor:

Each input has at least one dimension.
Match the two input dimensions from back to front, the dimension sizes must either be equal, one of them is 1, or one of them does not exist.

Where, z = x - y, the shapes of x and y are broadcastable, then the shape of z can be obtained as follows:

1. If the number of dimensions of x and y are not equal, prepend 1 to the dimensions of the tensor with fewer dimensions.

For example, The shape of x is [8, 1, 6, 1], the shape of y is [7, 1, 5], prepend 1 to the dimension of y.

x (4-D Tensor): 8 x 1 x 6 x 1

y (4-D Tensor): 1 x 7 x 1 x 5

2. Determine the size of each dimension of the output z: choose the maximum value from the two input dimensions.

z (4-D Tensor): 8 x 7 x 6 x 5

If the number of dimensions of the two inputs are the same, the size of the output can be directly determined in step 2. When p takes different values, the norm formula is as follows:

When p = 0, defining $0^0=0$, the zero-norm of z is simply the number of non-zero elements of z.

\[\begin{split}||z||_{0}=\lim_{p \\rightarrow 0}\sum_{i=1}^{m}|z_i|^{p}\end{split}\]

When p = inf, the inf-norm of z is the maximum element of the absolute value of z.

\[||z||_\infty=\max_i |z_i|\]

When p = -inf, the negative-inf-norm of z is the minimum element of the absolute value of z.

\[||z||_{-\infty}=\min_i |z_i|\]

Otherwise, the p-norm of z follows the formula,

\[\begin{split}||z||_{p}=(\sum_{i=1}^{m}|z_i|^p)^{\\frac{1}{p}}\end{split}\]

Parameters

x (Tensor) – 1-D to 6-D Tensor, its data type is bfloat16, float16, float32 or float64.
y (Tensor) – 1-D to 6-D Tensor, its data type is bfloat16, float16, float32 or float64.
p (float, optional) – The norm to be computed, its data type is float32 or float64. Default: 2.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor that is the p-norm of (x - y).

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([[3, 3],[3, 3]], dtype="float32")
>>> y = paddle.to_tensor([[3, 3],[3, 1]], dtype="float32")
>>> out = paddle.dist(x, y, 0)
>>> print(out)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
1.)

>>> out = paddle.dist(x, y, 2)
>>> print(out)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
2.)

>>> out = paddle.dist(x, y, float("inf"))
>>> print(out)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
2.)

>>> out = paddle.dist(x, y, float("-inf"))
>>> print(out)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
0.)

divide ( y: Tensor, name: str | None = None ) → Tensor [source] divide¶

Divide two tensors element-wise. The equation is:

\[out = x / y\]

Note

paddle.divide supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
y (Tensor) – the input tensor, it’s data type should be bool, bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 4], dtype='float64')
>>> y = paddle.to_tensor([1, 5, 2], dtype='float64')
>>> z = paddle.divide(x, y)
>>> print(z)
Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True,
[2.        , 0.60000000, 2.        ])

divide_ ( y: Tensor, name: str | None = None ) → Tensor [source] divide_¶: Inplace version of divide API, the output Tensor will be inplaced with input x. Please refer to divide.

dot ( y: Tensor, name: str | None = None ) → Tensor [source] dot¶

This operator calculates inner product for vectors.

Note

Support 1-d and 2-d Tensor. When it is 2d, the first dimension of this matrix is the batch dimension, which means that the vectors of multiple batches are dotted.

Parameters

x (Tensor) – 1-D or 2-D Tensor. Its dtype should be float32, float64, int32, int64, complex64, complex128
y (Tensor) – 1-D or 2-D Tensor. Its dtype should be float32, float64, int32, int64, complex64, complex128
name (str|None, optional) – Name of the output. Default is None. It’s used to print debug info for developers. Details: Name

Returns

the calculated result Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> # 1-D Tensor * 1-D Tensor
>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([4, 5, 6])
>>> z = paddle.dot(x, y)
>>> print(z)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
32)

>>> # 2-D Tensor * 2-D Tensor
>>> x = paddle.to_tensor([[1, 2, 3], [2, 4, 6]])
>>> y = paddle.to_tensor([[4, 5, 6], [4, 5, 6]])
>>> z = paddle.dot(x, y)
>>> print(z)
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[32, 64])

dsplit ( num_or_indices: int | Sequence[int], name: str | None = None ) → list[Tensor] [source] dsplit¶

dsplit Full name Depth Split, splits the input Tensor into multiple sub-Tensors along the depth axis, which is equivalent to paddle.tensor_split with axis=2.

Note

Make sure that the number of Tensor dimensions transformed using paddle.dsplit must be no less than 3.

In the following figure, Tenser x has shape [4, 4, 4], and after paddle.dsplit(x, num_or_indices=2) transformation, we get out0 and out1 sub-Tensors whose shapes are both [4, 4, 2] :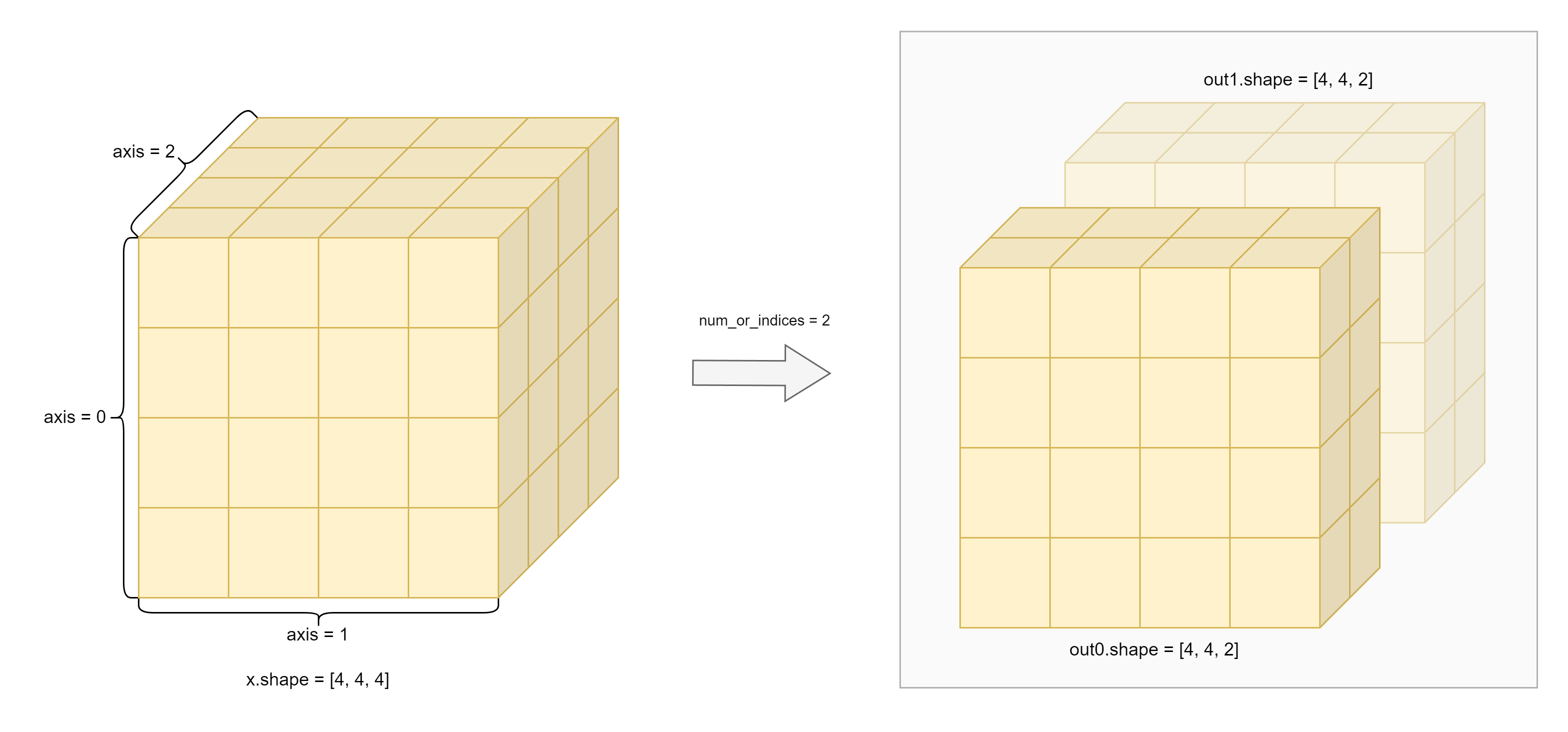

https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/dsplit/dsplit.png

Parameters

x (Tensor) – A Tensor whose dimension must be greater than 2. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If num_or_indices is an int n, x is split into n sections. If num_or_indices is a list or tuple of integer indices, x is split at each of the indices.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

list[Tensor], The list of segmented Tensors.

Examples

>>> import paddle

>>> # x is a Tensor of shape [7, 6, 8]
>>> x = paddle.rand([7, 6, 8])
>>> out0, out1 = paddle.dsplit(x, num_or_indices=2)
>>> print(out0.shape)
[7, 6, 4]
>>> print(out1.shape)
[7, 6, 4]

>>> out0, out1, out2 = paddle.dsplit(x, num_or_indices=[1, 4])
>>> print(out0.shape)
[7, 6, 1]
>>> print(out1.shape)
[7, 6, 3]
>>> print(out2.shape)
[7, 6, 4]

dtype [source]

Tensor’s data type.

Returns: dtype.
Return type: paddle dtype

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> print(x.dtype)
paddle.int64

eig ( name: str | None = None ) → tuple[Tensor, Tensor] eig¶

Performs the eigenvalue decomposition of a square matrix or a batch of square matrices.

Note

If the matrix is a Hermitian or a real symmetric matrix, please use eigh instead, which is much faster.
If only eigenvalues is needed, please use eigvals instead.
If the matrix is of any shape, please use svd.
This API is only supported on CPU device.
The output datatype is always complex for both real and complex input.

Parameters

x (Tensor) – A tensor with shape math:[*, N, N], The data type of the x should be one of float32, float64, compplex64 or complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

A tensor with shape math:[*, N] refers to the eigen values. Eigenvectors(Tensor): A tensor with shape math:[*, N, N] refers to the eigen vectors.

Return type

Eigenvalues(Tensor)

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.6707249, 7.2249975, 6.5045543],
...                       [9.956216,  8.749598,  6.066444 ],
...                       [4.4251957, 1.7983172, 0.370647 ]])
>>> w, v = paddle.linalg.eig(x)
>>> print(v)
Tensor(shape=[3, 3], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[ (0.5061365365982056+0j) ,  (0.7971761226654053+0j) ,
   (0.1851806491613388+0j) ],
 [ (0.8308236598968506+0j) , (-0.3463813066482544+0j) ,
   (-0.6837005615234375+0j) ],
 [ (0.23142573237419128+0j), (-0.49449989199638367+0j),
   (0.7058765292167664+0j) ]])

>>> print(w)
Tensor(shape=[3], dtype=complex64, place=Place(cpu), stop_gradient=True,
[ (16.50470733642578+0j)  , (-5.503481388092041+0j)  ,
  (-0.21026138961315155+0j)])

eigvals ( name: str | None = None ) → Tensor eigvals¶

Compute the eigenvalues of one or more general matrices.

Warning

The gradient kernel of this operator does not yet developed. If you need back propagation through this operator, please replace it with paddle.linalg.eig.

Parameters

x (Tensor) – A square matrix or a batch of square matrices whose eigenvalues will be computed. Its shape should be [*, M, M], where * is zero or more batch dimensions. Its data type should be float32, float64, complex64, or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A tensor containing the unsorted eigenvalues which has the same batch dimensions with x. The eigenvalues are complex-valued even when x is real.

Examples

>>> import paddle
>>> paddle.seed(2023)

>>> x = paddle.rand(shape=[3, 3], dtype='float64')
>>> print(x)
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0.86583615, 0.52014721, 0.25960938],
 [0.90525323, 0.42400090, 0.40641288],
 [0.97020893, 0.74437359, 0.51785128]])

>>> print(paddle.linalg.eigvals(x))
Tensor(shape=[3], dtype=complex128, place=Place(cpu), stop_gradient=True,
[ (1.788956694280852+0j)  ,  (0.16364484879581526+0j),
  (-0.14491322408727625+0j)])

eigvalsh ( UPLO: Literal['L', 'U'] = 'L', name: str | None = None ) → Tensor [source] eigvalsh¶

Computes the eigenvalues of a complex Hermitian (conjugate symmetric) or a real symmetric matrix.

Parameters

x (Tensor) – A tensor with shape $[*, M, M]$ , where * is zero or greater batch dimension. The data type of the input Tensor x should be one of float32, float64, complex64, complex128.
UPLO (str, optional) – Lower triangular part of a (‘L’, default) or the upper triangular part (‘U’).
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The tensor eigenvalues in ascending order.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, -2j], [2j, 5]])
>>> out_value = paddle.eigvalsh(x, UPLO='L')
>>> print(out_value)
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.17157286, 5.82842731])

element_size ( ) element_size¶

Returns the size in bytes of an element in the Tensor.

Returns: int, The size in bytes of an element in the Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor(1, dtype='bool')
>>> x.element_size()
1

>>> x = paddle.to_tensor(1, dtype='float16')
>>> x.element_size()
2

>>> x = paddle.to_tensor(1, dtype='float32')
>>> x.element_size()
4

>>> x = paddle.to_tensor(1, dtype='float64')
>>> x.element_size()
8

>>> x = paddle.to_tensor(1, dtype='complex128')
>>> x.element_size()
16

equal ( y: Tensor, name: str | None = None ) → Tensor [source] equal¶

This layer returns the truth value of $x == y$ elementwise.

Note

The output has no gradient.

Parameters

x (Tensor) – Tensor, data type is bool, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Tensor, data type is bool, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

output Tensor, it’s shape is the same as the input’s Tensor, and the data type is bool. The result of this op is stop_gradient.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 3, 2])
>>> result1 = paddle.equal(x, y)
>>> print(result1)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False, False])

equal_ ( y: Tensor, name: str | None = None ) → Tensor [source] equal_¶: Inplace version of equal API, the output Tensor will be inplaced with input x. Please refer to equal.

equal_all ( y: Tensor, name: str | None = None ) → Tensor [source] equal_all¶

Returns the truth value of $x == y$. True if two inputs have the same elements, False otherwise.

Note

The output has no gradient.

Parameters

x (Tensor) – Tensor, data type is bool, float32, float64, int32, int64.
y (Tensor) – Tensor, data type is bool, float32, float64, int32, int64.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

output Tensor, data type is bool, value is [False] or [True].

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 2, 3])
>>> z = paddle.to_tensor([1, 4, 3])
>>> result1 = paddle.equal_all(x, y)
>>> print(result1)
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
True)
>>> result2 = paddle.equal_all(x, z)
>>> print(result2)
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
False)

erf ( name: str | None = None ) → Tensor [source] erf¶

The error function. For more details, see Error function.

Equation:: \[out = \frac{2}{\sqrt{\pi}} \int_{0}^{x}e^{- \eta^{2}}d\eta\]

Parameters

x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

float32 or float64 (integer types are autocasted into float32), shape: the same as the input.

Return type

Tensor. The output of Erf, dtype

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.erf(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.42839241, -0.22270259,  0.11246292,  0.32862678])

erfinv ( name: str | None = None ) → Tensor [source] erfinv¶

The inverse error function of x. Please refer to erf

\[erfinv(erf(x)) = x.\]

Parameters

x (Tensor) – An N-D Tensor, the data type is float16, bfloat16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), an N-D Tensor, the shape and data type is the same with input: (integer types are autocasted into float32).

Example

>>> import paddle

>>> x = paddle.to_tensor([0, 0.5, -1.], dtype="float32")
>>> out = paddle.erfinv(x)
>>> out
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 0.       , 0.47693631, -inf.     ])

erfinv_ ( name: str | None = None ) → Tensor erfinv_¶: Inplace version of erfinv API, the output Tensor will be inplaced with input x. Please refer to erfinv.

exp ( name: str | None = None ) → Tensor [source] exp¶

Computes exp of x element-wise with a natural number e as the base.

\[out = e^x\]

Parameters

x (Tensor) – Input of Exp operator, an N-D Tensor, with data type int32, int64, bfloat16, float16, float32, float64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Exp operator, a Tensor with shape same as input.

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.exp(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.67032003, 0.81873077, 1.10517097, 1.34985888])

exp_ ( name=None ) exp_¶: Inplace version of exp API, the output Tensor will be inplaced with input x. Please refer to exp.

expand ( shape: ShapeLike, name: str | None = None ) → Tensor [source] expand¶

Expand the input tensor to a given shape.

Both the number of dimensions of x and the number of elements in shape should be less than or equal to 6. And the number of dimensions of x should be less than the number of elements in shape. The dimension to expand must have a value 0.

The image illustrates a typical case of the expand operation. The Original Tensor is a 1D tensor with shape [3] and values [1, 2, 3]. Using the paddle.expand method with the parameter shape = [2, 3], it is broadcasted and expanded into a 2D tensor with shape [2, 3]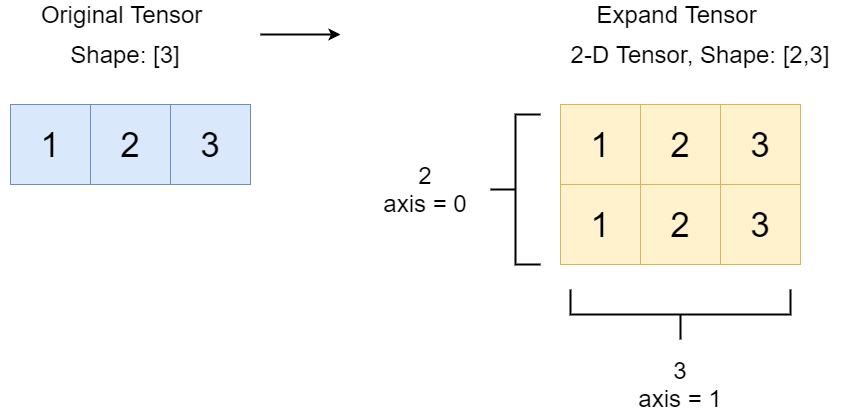

Parameters

x (Tensor) – The input Tensor, its data type is bool, float16, float32, float64, int32, int64, uint8, uint16, complex64 or complex128.
shape (list|tuple|Tensor) – The result shape after expanding. The data type is int32. If shape is a list or tuple, all its elements should be integers or 0-D or 1-D Tensors with the data type int32. If shape is a Tensor, it should be an 1-D Tensor with the data type int32. The value -1 in shape means keeping the corresponding dimension unchanged.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

N-D Tensor, A Tensor with the given shape. The data type is the same as x.

Examples

>>> import paddle

>>> data = paddle.to_tensor([1, 2, 3], dtype='int32')
>>> out = paddle.expand(data, shape=[2, 3])
>>> print(out)
Tensor(shape=[2, 3], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 2, 3],
 [1, 2, 3]])

expand_as ( y: Tensor, name: str | None = None ) → Tensor [source] expand_as¶

Expand the input tensor x to the same shape as the input tensor y.

Both the number of dimensions of x and y must be less than or equal to 6, and the number of dimensions of y must be greater than or equal to that of x. The dimension to expand must have a value of 0.

The following diagram illustrates how a one-dimensional tensor is transformed into a tensor with a shape of [2,3] through the expand_as operation. The target tensor has a shape of [2,3], and through expand_as, the one-dimensional tensor is expanded into a tensor with a shape of [2,3].

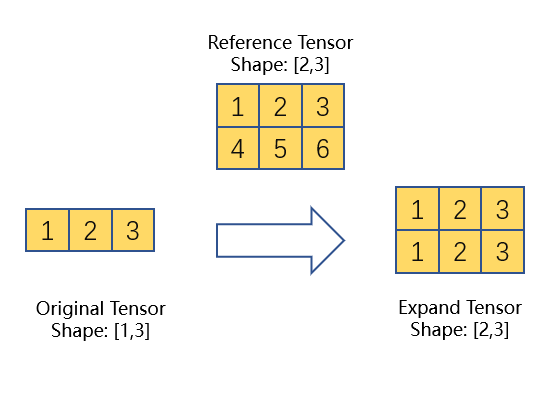
Parameters

x (Tensor) – The input tensor, its data type is bool, float32, float64, int32 or int64.
y (Tensor) – The input tensor that gives the shape to expand to.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

N-D Tensor, A Tensor with the same shape as y. The data type is the same as x.

Examples

>>> import paddle

>>> data_x = paddle.to_tensor([1, 2, 3], 'int32')
>>> data_y = paddle.to_tensor([[1, 2, 3], [4, 5, 6]], 'int32')
>>> out = paddle.expand_as(data_x, data_y)
>>> print(out)
Tensor(shape=[2, 3], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 2, 3],
 [1, 2, 3]])

expm1 ( name: str | None = None ) → Tensor [source] expm1¶

Expm1 Operator. Computes expm1 of x element-wise with a natural number $e$ as the base.

\[out = e^x - 1\]

Parameters

x (Tensor) – Input of Expm1 operator, an N-D Tensor, with data type int32, int64, bfloat16, float16, float32, float64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Expm1 operator, a Tensor with shape same as input.

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.expm1(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.32967997, -0.18126924,  0.10517092,  0.34985882])

exponential_ ( lam: float = 1.0, name: str | None = None ) → Tensor exponential_¶

This inplace OP fill input Tensor x with random number from a Exponential Distribution.

lam is $\lambda$ parameter of Exponential Distribution.

\[f(x) = \lambda e^{-\lambda x}\]

Parameters

x (Tensor) – Input tensor. The data type should be float32, float64.
lam (float, optional) – $\lambda$ parameter of Exponential Distribution. Default, 1.0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, Input Tensor x.

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> paddle.seed(100)

>>> x = paddle.empty([2,3])
>>> x.exponential_()
>>> 
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.80643415, 0.23211166, 0.01169797],
 [0.72520679, 0.45208144, 0.30234432]])
>>> 

fill_ ( value: float ) → Tensor fill_¶

Notes:: This API is ONLY available in Dygraph mode

This function fill the Tensor with value inplace.

Parameters

x (Tensor) – x is the Tensor we want to filled data inplace
value (int|float) – value is the value to be filled in x

Returns

x(Tensor), Tensor x filled with value inplace

Examples

>>> import paddle

>>> tensor = paddle.to_tensor([0, 1, 2, 3, 4])

>>> tensor.fill_(0)
>>> print(tensor.tolist())
[0, 0, 0, 0, 0]

fill_diagonal_ ( value: float, offset: int = 0, wrap: bool = False, name: str | None = None ) → Tensor fill_diagonal_¶

Note

This API is ONLY available in Dygraph mode.

This function fill the value into the x Tensor’s diagonal inplace.

Parameters

x (Tensor) – x is the original Tensor
value (int|float) – value is the value to filled in x
offset (int,optional) – the offset to the main diagonal. Default: 0 (main diagonal).
wrap (bool,optional) – the diagonal ‘wrapped’ after N columns for tall matrices.
name (str|None,optional) – Name for the operation (optional, default is None)

Returns

Tensor, Tensor with diagonal filled with value.

Examples

>>> import paddle
>>> x = paddle.ones((4, 3)) * 2
>>> x.fill_diagonal_(1.0)
>>> print(x.tolist())
[[1.0, 2.0, 2.0], [2.0, 1.0, 2.0], [2.0, 2.0, 1.0], [2.0, 2.0, 2.0]]

fill_diagonal_tensor ( y: Tensor, offset: int = 0, dim1: int = 0, dim2: int = 1, name: str | None = None ) → Tensor fill_diagonal_tensor¶

This function fill the source Tensor y into the x Tensor’s diagonal.

Parameters

x (Tensor) – x is the original Tensor
y (Tensor) – y is the Tensor to filled in x
dim1 (int,optional) – first dimension with respect to which to fill diagonal. Default: 0.
dim2 (int,optional) – second dimension with respect to which to fill diagonal. Default: 1.
offset (int,optional) – the offset to the main diagonal. Default: 0 (main diagonal).
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Tensor with diagonal filled with y.

Examples

>>> import paddle

>>> x = paddle.ones((4, 3)) * 2
>>> y = paddle.ones((3,))
>>> nx = x.fill_diagonal_tensor(y)
>>> print(nx.tolist())
[[1.0, 2.0, 2.0], [2.0, 1.0, 2.0], [2.0, 2.0, 1.0], [2.0, 2.0, 2.0]]

fill_diagonal_tensor_ ( y: Tensor, offset: int = 0, dim1: int = 0, dim2: int = 1, name: str | None = None ) → Tensor fill_diagonal_tensor_¶

Note

This API is ONLY available in Dygraph mode.

This function fill the source Tensor y into the x Tensor’s diagonal inplace.

Parameters

x (Tensor) – x is the original Tensor
y (Tensor) – y is the Tensor to filled in x
dim1 (int,optional) – first dimension with respect to which to fill diagonal. Default: 0.
dim2 (int,optional) – second dimension with respect to which to fill diagonal. Default: 1.
offset (int,optional) – the offset to the main diagonal. Default: 0 (main diagonal).
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Tensor with diagonal filled with y.

Examples

>>> import paddle

>>> x = paddle.ones((4, 3)) * 2
>>> y = paddle.ones((3,))
>>> x.fill_diagonal_tensor_(y)
>>> print(x.tolist())
[[1.0, 2.0, 2.0], [2.0, 1.0, 2.0], [2.0, 2.0, 1.0], [2.0, 2.0, 2.0]]

flatten ( start_axis: int = 0, stop_axis: int = -1, name: str | None = None ) → Tensor [source] flatten¶

Flattens a contiguous range of axes in a tensor according to start_axis and stop_axis.

Note

The output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode. If you want to use the Tensor copy version, please use Tensor.clone like flatten_clone_x = x.flatten().clone().

For Example:

Case 1:

  Given
    X.shape = (3, 100, 100, 4)

  and
    start_axis = 1
    end_axis = 2

  We get:
    Out.shape = (3, 100 * 100, 4)

Case 2:

  Given
    X.shape = (3, 100, 100, 4)

  and
    start_axis = 0
    stop_axis = -1

  We get:
    Out.shape = (3 * 100 * 100 * 4)

Parameters

x (Tensor) – A tensor of number of dimensions >= axis. A tensor with data type float16, float32, float64, int8, int32, int64, uint8.
start_axis (int) – the start axis to flatten
stop_axis (int) – the stop axis to flatten
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A tensor with the contents of the input tensor, whose input axes are flattened by indicated start_axis and end_axis, and data type is the same as input x.

Examples

>>> import paddle

>>> image_shape=(2, 3, 4, 4)

>>> x = paddle.arange(end=image_shape[0] * image_shape[1] * image_shape[2] * image_shape[3])
>>> img = paddle.reshape(x, image_shape)

>>> out = paddle.flatten(img, start_axis=1, stop_axis=2)
>>> print(out.shape)
[2, 12, 4]

>>> # out shares data with img in dygraph mode
>>> img[0, 0, 0, 0] = -1
>>> print(out[0, 0, 0])
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
-1)

flatten_ ( start_axis: int = 0, stop_axis: int = -1, name: str | None = None ) → Tensor [source] flatten_¶: Inplace version of flatten API, the output Tensor will be inplaced with input x. Please refer to flatten.

flip ( axis: Sequence[int] | int, name: str | None = None ) → Tensor [source] flip¶

Reverse the order of a n-D tensor along given axis in axis.

The image below illustrates how flip works.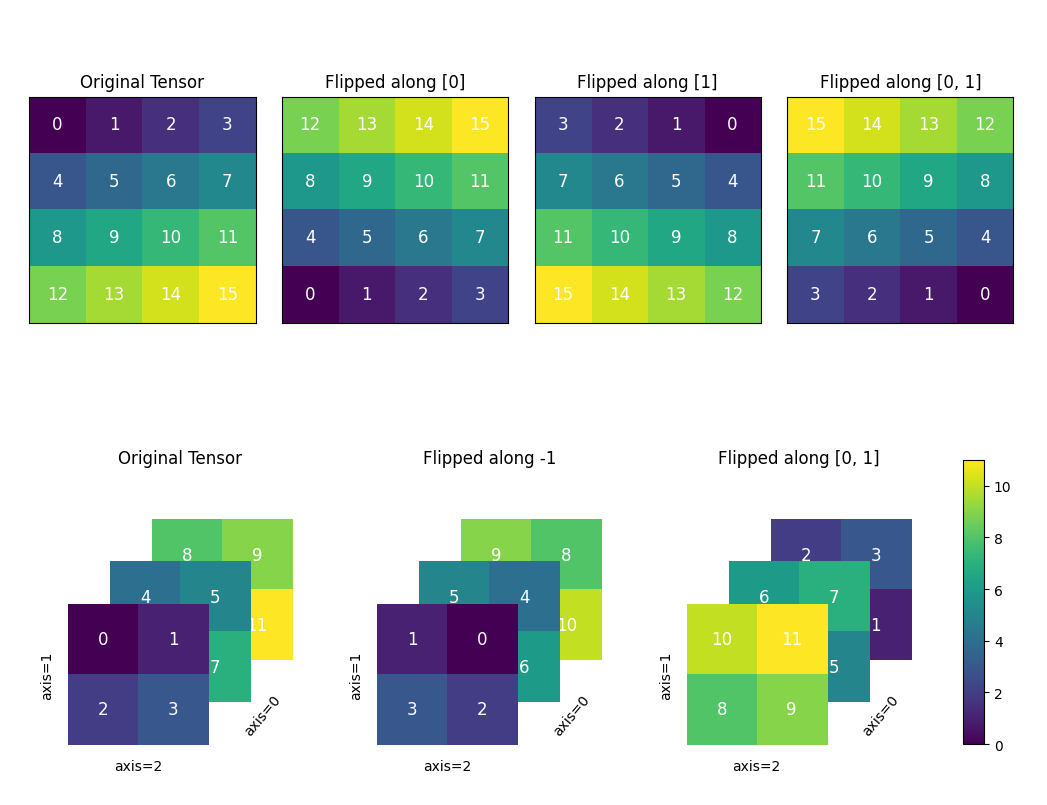

Parameters

x (Tensor) – A Tensor with shape $[N_1, N_2,..., N_k]$ . The data type of the input Tensor x should be float32, float64, int32, int64, bool.
axis (list|tuple|int) – The axis(axes) to flip on. Negative indices for indexing from the end are accepted.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Tensor or DenseTensor calculated by flip layer. The data type is same with input x.

Examples

>>> 
>>> import paddle

>>> image_shape=(3, 2, 2)
>>> img = paddle.arange(image_shape[0] * image_shape[1] * image_shape[2]).reshape(image_shape)
>>> tmp = paddle.flip(img, [0,1])
>>> print(tmp)
Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[10, 11],
  [8 , 9 ]],
 [[6 , 7 ],
  [4 , 5 ]],
 [[2 , 3 ],
  [0 , 1 ]]])

>>> out = paddle.flip(tmp,-1)
>>> print(out)
Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[11, 10],
  [9 , 8 ]],
 [[7 , 6 ],
  [5 , 4 ]],
 [[3 , 2 ],
  [1 , 0 ]]])

floor ( name: str | None = None ) → Tensor [source] floor¶

Floor Activation Operator. Computes floor of x element-wise.

\[out = \lfloor x \rfloor\]

Parameters

x (Tensor) – Input of Floor operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Floor operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.floor(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-1., -1.,  0.,  0.])

floor_ ( name=None ) floor_¶: Inplace version of floor API, the output Tensor will be inplaced with input x. Please refer to floor.

floor_divide ( y: Tensor, name: str | None = None ) → Tensor [source] floor_divide¶

Floor divide two tensors element-wise and rounds the quotinents to the nearest integer toward negative infinite. The equation is:

\[out = floor(x / y)\]

$x$: Multidimensional Tensor.
$y$: Multidimensional Tensor.

Note

paddle.floor_divide supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be uint8, int8, int32, int64, float32, float64, float16, bfloat16.
y (Tensor) – the input tensor, it’s data type should be uint8, int8, int32, int64, float32, float64, float16, bfloat16.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. It’s dimension equals with $x$.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 8, 7])
>>> y = paddle.to_tensor([1, 5, 3, 3])
>>> z = paddle.floor_divide(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[2, 0, 2, 2])

>>> x = paddle.to_tensor([2, 3, 8, 7])
>>> y = paddle.to_tensor([1, -5, -3, -3])
>>> z = paddle.floor_divide(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[2, -1, -3, -3])

floor_divide_ ( y: Tensor, name: str | None = None ) → Tensor [source] floor_divide_¶: Inplace version of floor_divide API, the output Tensor will be inplaced with input x. Please refer to floor_divide.

floor_mod ( y: Tensor, name: str | None = None ) → Tensor [source] floor_mod¶

Mod two tensors element-wise. The equation is:

\[out = x \% y\]

Note

paddle.remainder supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

And mod, floor_mod are all functions with the same name

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 8, 7])
>>> y = paddle.to_tensor([1, 5, 3, 3])
>>> z = paddle.remainder(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

>>> z = paddle.floor_mod(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

>>> z = paddle.mod(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

floor_mod_ ( y: Tensor, name: str | None = None ) → Tensor floor_mod_¶: Inplace version of floor_mod_ API, the output Tensor will be inplaced with input x. Please refer to floor_mod_.

fmax ( y: Tensor, name: str | None = None ) → Tensor [source] fmax¶

Compares the elements at the corresponding positions of the two tensors and returns a new tensor containing the maximum value of the element. If one of them is a nan value, the other value is directly returned, if both are nan values, then the first nan value is returned. The equation is:

\[out = fmax(x, y)\]

Note

paddle.fmax supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2], [7, 8]])
>>> y = paddle.to_tensor([[3, 4], [5, 6]])
>>> res = paddle.fmax(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 4],
 [7, 8]])

>>> x = paddle.to_tensor([[1, 2, 3], [1, 2, 3]])
>>> y = paddle.to_tensor([3, 0, 4])
>>> res = paddle.fmax(x, y)
>>> print(res)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 2, 4],
 [3, 2, 4]])

>>> x = paddle.to_tensor([2, 3, 5], dtype='float32')
>>> y = paddle.to_tensor([1, float("nan"), float("nan")], dtype='float32')
>>> res = paddle.fmax(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[2., 3., 5.])

>>> x = paddle.to_tensor([5, 3, float("inf")], dtype='float32')
>>> y = paddle.to_tensor([1, -float("inf"), 5], dtype='float32')
>>> res = paddle.fmax(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[5.  , 3.  , inf.])

fmin ( y: Tensor, name: str | None = None ) → Tensor [source] fmin¶

Compares the elements at the corresponding positions of the two tensors and returns a new tensor containing the minimum value of the element. If one of them is a nan value, the other value is directly returned, if both are nan values, then the first nan value is returned. The equation is:

\[out = fmin(x, y)\]

Note

paddle.fmin supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2], [7, 8]])
>>> y = paddle.to_tensor([[3, 4], [5, 6]])
>>> res = paddle.fmin(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 2],
 [5, 6]])

>>> x = paddle.to_tensor([[[1, 2, 3], [1, 2, 3]]])
>>> y = paddle.to_tensor([3, 0, 4])
>>> res = paddle.fmin(x, y)
>>> print(res)
Tensor(shape=[1, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[1, 0, 3],
  [1, 0, 3]]])

>>> x = paddle.to_tensor([2, 3, 5], dtype='float32')
>>> y = paddle.to_tensor([1, float("nan"), float("nan")], dtype='float32')
>>> res = paddle.fmin(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1., 3., 5.])

>>> x = paddle.to_tensor([5, 3, float("inf")], dtype='float64')
>>> y = paddle.to_tensor([1, -float("inf"), 5], dtype='float64')
>>> res = paddle.fmin(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True,
[ 1.  , -inf.,  5.  ])

frac ( name: str | None = None ) → Tensor [source] frac¶

This API is used to return the fractional portion of each element in input.

Parameters

x (Tensor) – The input tensor, which data type should be int32, int64, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output Tensor of frac.

Return type

Tensor

Examples

>>> import paddle

>>> input = paddle.to_tensor([[12.22000003, -1.02999997],
...                           [-0.54999995, 0.66000003]])
>>> output = paddle.frac(input)
>>> output
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 0.22000003, -0.02999997],
 [-0.54999995,  0.66000003]])

frac_ ( name: str | None = None ) → Tensor [source] frac_¶: Inplace version of frac API, the output Tensor will be inplaced with input x. Please refer to frac.

frexp ( name: str | None = None ) → tuple[Tensor, Tensor] [source] frexp¶

The function used to decompose a floating point number into mantissa and exponent.

Parameters

x (Tensor) – The input tensor, it’s data type should be float32, float64.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

mantissa (Tensor), A mantissa Tensor. The shape and data type of mantissa tensor and exponential tensor are

the same as those of input.
exponent (Tensor), A exponent Tensor. The shape and data type of mantissa tensor and exponential tensor are

the same as those of input.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2, 3, 4]], dtype="float32")
>>> mantissa, exponent = paddle.tensor.math.frexp(x)
>>> mantissa
Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.50000000, 0.50000000, 0.75000000, 0.50000000]])
>>> exponent
Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 2., 2., 3.]])

gammainc ( y: Tensor, name: str | None = None ) → Tensor [source] gammainc¶

Computes the regularized lower incomplete gamma function.

\[P(x, y) = \frac{1}{\Gamma(x)} \int_{0}^{y} t^{x-1} e^{-t} dt\]

Parameters

x (Tensor) – The non-negative argument Tensor. Must be one of the following types: float32, float64.
y (Tensor) – The positive parameter Tensor. Must be one of the following types: float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the gammainc of the input Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([0.5, 0.5, 0.5, 0.5, 0.5], dtype="float32")
>>> y = paddle.to_tensor([0, 1, 10, 100, 1000], dtype="float32")
>>> out = paddle.gammainc(x, y)
>>> print(out)
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
    [0.        , 0.84270084, 0.99999225, 1.        , 1.        ])

gammainc_ ( y: Tensor, name: str | None = None ) → Tensor [source] gammainc_¶: Inplace version of gammainc API, the output Tensor will be inplaced with input x. Please refer to gammainc.

gammaincc ( y: Tensor, name: str | None = None ) → Tensor [source] gammaincc¶

Computes the regularized upper incomplete gamma function.

\[Q(x, y) = \frac{1}{\Gamma(x)} \int_{y}^{\infty} t^{x-1} e^{-t} dt\]

Parameters

x (Tensor) – The non-negative argument Tensor. Must be one of the following types: float32, float64.
y (Tensor) – The positive parameter Tensor. Must be one of the following types: float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the gammaincc of the input Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([0.5, 0.5, 0.5, 0.5, 0.5], dtype="float32")
>>> y = paddle.to_tensor([0, 1, 10, 100, 1000], dtype="float32")
>>> out = paddle.gammaincc(x, y)
>>> print(out)
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
    [1.        , 0.15729916, 0.00000774, 0.        , 0.        ])

gammaincc_ ( y: Tensor, name: str | None = None ) → Tensor [source] gammaincc_¶: Inplace version of gammaincc API, the output Tensor will be inplaced with input x. Please refer to gammaincc.

gammaln ( name: str | None = None ) → Tensor [source] gammaln¶

Calculates the logarithm of the absolute value of the gamma function elementwisely.

Parameters

x (Tensor) – Input Tensor. Must be one of the following types: float16, float32, float64, bfloat16.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, The values of the logarithm of the absolute value of the gamma at the given tensor x.

Examples

>>> import paddle

>>> x = paddle.arange(1.5, 4.5, 0.5)
>>> out = paddle.gammaln(x)
>>> print(out)
Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True,
    [-0.12078224,  0.        ,  0.28468287,  0.69314718,  1.20097363,
        1.79175949])

gammaln_ ( name: str | None = None ) → Tensor [source] gammaln_¶: Inplace version of gammaln API, the output Tensor will be inplaced with input x. Please refer to gammaln.

gather ( index: Tensor, axis: Tensor | int | None = None, name: str | None = None ) → Tensor [source] gather¶

Output is obtained by gathering entries of axis of x indexed by index and concatenate them together.

Given:

x = [[1, 2],
     [3, 4],
     [5, 6]]

index = [1, 2]
axis=[0]

Then:

out = [[3, 4],
       [5, 6]]

Parameters

x (Tensor) – The source input tensor with rank>=1. Supported data type is int32, int64, float32, float64, complex64, complex128 and uint8 (only for CPU), float16 (only for GPU).
index (Tensor) – The index input tensor with rank=0 or rank=1. Data type is int32 or int64.
axis (Tensor|int|None, optional) – The axis of input to be gathered, it’s can be int or a Tensor with data type is int32 or int64. The default value is None, if None, the axis is 0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

output (Tensor), If the index is a 1-D tensor, the output is a tensor with the same shape as x. If the index is a 0-D tensor, the output will reduce the dimension where the axis pointing.

Examples

>>> import paddle

>>> input = paddle.to_tensor([[1,2],[3,4],[5,6]])
>>> index = paddle.to_tensor([0,1])
>>> output = paddle.gather(input, index, axis=0)
>>> print(output)
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 2],
 [3, 4]])

gather_nd ( index: Tensor, name: str | None = None ) → Tensor [source] gather_nd¶

This function is actually a high-dimensional extension of gather and supports for simultaneous indexing by multiple axes. index is a K-dimensional integer tensor, which is regarded as a (K-1)-dimensional tensor of index into input, where each element defines a slice of params:

\[output[(i_0, ..., i_{K-2})] = input[index[(i_0, ..., i_{K-2})]]\]

Obviously, index.shape[-1] <= input.rank . And, the output tensor has shape index.shape[:-1] + input.shape[index.shape[-1]:] .

Given:
    x =  [[[ 0,  1,  2,  3],
           [ 4,  5,  6,  7],
           [ 8,  9, 10, 11]],
          [[12, 13, 14, 15],
           [16, 17, 18, 19],
           [20, 21, 22, 23]]]
    x.shape = (2, 3, 4)

* Case 1:
    index = [[1]]

    gather_nd(x, index)
             = [x[1, :, :]]
             = [[12, 13, 14, 15],
                [16, 17, 18, 19],
                [20, 21, 22, 23]]

* Case 2:
    index = [[0,2]]

    gather_nd(x, index)
             = [x[0, 2, :]]
             = [8, 9, 10, 11]

* Case 3:
    index = [[1, 2, 3]]

    gather_nd(x, index)
             = [x[1, 2, 3]]
             = [23]

Parameters

x (Tensor) – The input Tensor which it’s data type should be bool, float16, float32, float64, int32, int64.
index (Tensor) – The index input with rank > 1, index.shape[-1] <= input.rank. Its dtype should be int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

-1] + input.shape[index.shape[-1]:]

Return type

output (Tensor), A tensor with the shape index.shape[

Examples

>>> import paddle

>>> x = paddle.to_tensor([[[1, 2], [3, 4], [5, 6]],
...                       [[7, 8], [9, 10], [11, 12]]])
>>> index = paddle.to_tensor([[0, 1]])

>>> output = paddle.gather_nd(x, index)
>>> print(output)
Tensor(shape=[1, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 4]])

gcd ( y: Tensor, name: str | None = None ) → Tensor [source] gcd¶

Computes the element-wise greatest common divisor (GCD) of input |x| and |y|. Both x and y must have integer types.

Note

gcd(0,0)=0, gcd(0, y)=|y|

If x.shape != y.shape, they must be broadcastable to a common shape (which becomes the shape of the output).

Parameters

x (Tensor) – An N-D Tensor, the data type is int32, int64.
y (Tensor) – An N-D Tensor, the data type is int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor, the data type is the same with input.

Return type

out (Tensor)

Examples

>>> import paddle

>>> x1 = paddle.to_tensor(12)
>>> x2 = paddle.to_tensor(20)
>>> paddle.gcd(x1, x2)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
4)

>>> x3 = paddle.arange(6)
>>> paddle.gcd(x3, x2)
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[20, 1 , 2 , 1 , 4 , 5])

>>> x4 = paddle.to_tensor(0)
>>> paddle.gcd(x4, x2)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
20)

>>> paddle.gcd(x4, x4)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
0)

>>> x5 = paddle.to_tensor(-20)
>>> paddle.gcd(x1, x5)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
4)

gcd_ ( y: Tensor, name: str | None = None ) → Tensor [source] gcd_¶: Inplace version of gcd API, the output Tensor will be inplaced with input x. Please refer to gcd.

geometric_ ( probs: float | paddle.Tensor, name: str | None = None ) → Tensor [source] geometric_¶

Fills the tensor with numbers drawn from the Geometric distribution.

Parameters

x (Tensor) – the tensor will be filled, The data type is float32 or float64.
probs (float|Tensor) – Probability parameter. The value of probs must be positive. When the parameter is a tensor, probs is probability of success for each trial.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

input tensor with numbers drawn from the Geometric distribution.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.randn([3, 4])
>>> x.geometric_(0.3)
>>> 
>>> print(x)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[2.42739224, 4.78268528, 1.23302543, 3.76555204],
 [1.38877118, 0.16075331, 0.16401523, 2.47349310],
 [1.72872102, 2.76533413, 0.33410925, 1.63351011]])

get_strides ( ) get_strides¶

Returns the strides of current Tensor.

Returns: List, the strides of current Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = x[1]
>>> print(y.get_strides())
[]

get_tensor ( ) get_tensor¶

Returns the underline tensor in the origin Tensor.

Returns: Underline tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1.0], stop_gradient=False)
>>> underline_x = x.get_tensor()
>>> print(underline_x)
  - place: Place(cpu)
  - shape: [1]
  - layout: NCHW
  - dtype: float32
  - data: [1]

grad [source]

Tensor’s grad Tensor.

Returns: grad Tensor.
Return type: Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.0, stop_gradient=False)
>>> y = x**2
>>> y.backward()
>>> print(x.grad)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
2.)

>>> x.grad = paddle.to_tensor(3.0)
>>> print(x.grad)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=False,
3.)

gradient ( ) → npt.NDArray[Any] | tuple[npt.NDArray[Any], npt.NDArray[Any]] | None gradient¶

Warning

API “paddle.base.dygraph.tensor_patch_methods.gradient” is deprecated since 2.1.0, and will be removed in future versions. Reason: Please use tensor.grad, which returns the tensor value of the gradient.

Warning

This API will be deprecated in the future, it is recommended to use x.grad which returns the tensor value of the gradient.

Get the Gradient of Current Tensor.

Returns: Numpy value of the gradient of current Tensor
Return type: ndarray

Examples

>>> import paddle

>>> x = paddle.to_tensor(5., stop_gradient=False)
>>> y = paddle.pow(x, 4.0)
>>> y.backward()
>>> print("grad of x: {}".format(x.gradient()))
grad of x: 500.0

greater_equal ( y: Tensor, name: str | None = None ) → Tensor [source] greater_equal¶

Returns the truth value of $x >= y$ elementwise, which is equivalent function to the overloaded operator >=.

Note

The output has no gradient.

Parameters

x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The output shape is same as input x. The output data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 3, 2])
>>> result1 = paddle.greater_equal(x, y)
>>> print(result1)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False, True ])

greater_equal_ ( y: Tensor, name: str | None = None ) → Tensor [source] greater_equal_¶: Inplace version of greater_equal API, the output Tensor will be inplaced with input x. Please refer to greater_equal.

greater_than ( y: Tensor, name: str | None = None ) → Tensor [source] greater_than¶

Returns the truth value of $x > y$ elementwise, which is equivalent function to the overloaded operator >.

Note

The output has no gradient.

Parameters

x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The output shape is same as input x. The output data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 3, 2])
>>> result1 = paddle.greater_than(x, y)
>>> print(result1)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, False, True ])

greater_than_ ( y: Tensor, name: str | None = None ) → Tensor [source] greater_than_¶: Inplace version of greater_than API, the output Tensor will be inplaced with input x. Please refer to greater_than.

heaviside ( y: Tensor, name: str | None = None ) → Tensor [source] heaviside¶

Computes the Heaviside step function determined by corresponding element in y for each element in x. The equation is

\[\begin{split}heaviside(x, y)= \left\{ \begin{array}{lcl} 0,& &\text{if} \ x < 0, \\ y,& &\text{if} \ x = 0, \\ 1,& &\text{if} \ x > 0. \end{array} \right.\end{split}\]

Note

paddle.heaviside supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – The input tensor of Heaviside step function, it’s data type should be bfloat16, float16, float32, float64, int32 or int64.
y (Tensor) – The tensor that determines a Heaviside step function, it’s data type should be bfloat16, float16, float32, float64, int32 or int64.
name (str|None, optional) – Name for the operation (optional, default is None). Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x and y have different shapes and are broadcastable, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle
>>> x = paddle.to_tensor([-0.5, 0, 0.5])
>>> y = paddle.to_tensor([0.1])
>>> paddle.heaviside(x, y)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.        , 0.10000000, 1.        ])
>>> x = paddle.to_tensor([[-0.5, 0, 0.5], [-0.5, 0.5, 0]])
>>> y = paddle.to_tensor([0.1, 0.2, 0.3])
>>> paddle.heaviside(x, y)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.        , 0.20000000, 1.        ],
 [0.        , 1.        , 0.30000001]])

histogram ( bins: int = 100, min: float = 0.0, max: float = 0.0, weight: Tensor | None = None, density: bool = False, name: str | None = None ) → Tensor [source] histogram¶

Computes the histogram of a tensor. The elements are sorted into equal width bins between min and max. If min and max are both zero, the minimum and maximum values of the data are used.

Parameters

input (Tensor) – A Tensor with shape $[N_1, N_2,..., N_k]$ . The data type of the input Tensor should be float32, float64, int32, int64.
bins (int, optional) – number of histogram bins. Default: 100.
min (float, optional) – lower end of the range (inclusive). Default: 0.0.
max (float, optional) – upper end of the range (inclusive). Default: 0.0.
weight (Tensor, optional) – If provided, it must have the same shape as input. Each value in input contributes its associated weight towards the bin count (instead of 1). Default: None.
density (bool, optional) – If False, the result will contain the count (or total weight) in each bin. If True, the result is the value of the probability density function over the bins, normalized such that the integral over the range of the bins is 1.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, shape is (nbins,), the counts or density of the histogram.

Examples

>>> import paddle

>>> inputs = paddle.to_tensor([1, 2, 1])
>>> result = paddle.histogram(inputs, bins=4, min=0, max=3)
>>> print(result)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 2, 1, 0])

histogram_bin_edges ( bins: int = 100, min: float = 0.0, max: float = 0.0, name: str | None = None ) → Tensor [source] histogram_bin_edges¶

Computes only the edges of the bins used by the histogram function. If min and max are both zero, the minimum and maximum values of the data are used.

Parameters

input (Tensor) – The data type of the input Tensor should be float32, float64, int32, int64.
bins (int, optional) – number of histogram bins.
min (float, optional) – lower end of the range (inclusive). Default: 0.0.
max (float, optional) – upper end of the range (inclusive). Default: 0.0.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, the values of the bin edges. The output data type will be float32.

Examples

>>> import paddle

>>> inputs = paddle.to_tensor([1, 2, 1])
>>> result = paddle.histogram_bin_edges(inputs, bins=4, min=0, max=3)
>>> print(result)
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.        , 0.75000000, 1.50000000, 2.25000000, 3.        ])

Computes a multi-dimensional histogram of the values in a tensor.

Interprets the elements of an input tensor whose innermost dimension has size N as a collection of N-dimensional points. Maps each of the points into a set of N-dimensional bins and returns the number of points (or total weight) in each bin.

input x must be a tensor with at least 2 dimensions. If input has shape (M, N), each of its M rows defines a point in N-dimensional space. If input has three or more dimensions, all but the last dimension are flattened.

Each dimension is independently associated with its own strictly increasing sequence of bin edges. Bin edges may be specified explicitly by passing a sequence of 1D tensors. Alternatively, bin edges may be constructed automatically by passing a sequence of integers specifying the number of equal-width bins in each dimension.

Parameters

x (Tensor) – The input tensor.
bins (list[Tensor], list[int], or int) – If list[Tensor], defines the sequences of bin edges. If list[int], defines the number of equal-width bins in each dimension. If int, defines the number of equal-width bins for all dimensions.
ranges (sequence[float]|None, optional) – Defines the leftmost and rightmost bin edges in each dimension. If is None, set the minimum and maximum as leftmost and rightmost edges for each dimension.
density (bool, optional) – If False (default), the result will contain the count (or total weight) in each bin. If True, each count (weight) is divided by the total count (total weight), then divided by the volume of its associated bin.
weights (Tensor, optional) – By default, each value in the input has weight 1. If a weight tensor is passed, each N-dimensional coordinate in input contributes its associated weight towards its bin’s result. The weight tensor should have the same shape as the input tensor excluding its innermost dimension N.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

N-dimensional Tensor containing the values of the histogram. bin_edges(Tensor[]), sequence of N 1D Tensors containing the bin edges.

Examples

>>> import paddle
>>> x = paddle.to_tensor([[0., 1.], [1., 0.], [2.,0.], [2., 2.]])
>>> bins = [3,3]
>>> weights = paddle.to_tensor([1., 2., 4., 8.])
>>> paddle.histogramdd(x, bins=bins, weights=weights)
(Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[0., 1., 0.],
        [2., 0., 0.],
        [4., 0., 8.]]), [Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.        , 0.66666669, 1.33333337, 2.        ]), Tensor(shape=[4], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.        , 0.66666669, 1.33333337, 2.        ])])

>>> import paddle
>>> y = paddle.to_tensor([[0., 0.], [1., 1.], [2., 2.]])
>>> bins = [2,2]
>>> ranges = [0., 1., 0., 1.]
>>> density = True
>>> paddle.histogramdd(y, bins=bins, ranges=ranges, density=density)
(Tensor(shape=[2, 2], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[2., 0.],
        [0., 2.]]), [Tensor(shape=[3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.        , 0.50000000, 1.        ]), Tensor(shape=[3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.        , 0.50000000, 1.        ])])

householder_product ( tau: Tensor, name: str | None = None ) → Tensor householder_product¶

Computes the first n columns of a product of Householder matrices.

This function can get the vector $\omega_{i}$ from matrix x (m x n), the $i-1$ elements are zeros, and the i-th is 1, the rest of the elements are from i-th column of x. And with the vector tau can calculate the first n columns of a product of Householder matrices.

$H_i = I_m - \tau_i \omega_i \omega_i^H$

Parameters

x (Tensor) – A tensor with shape (*, m, n) where * is zero or more batch dimensions.
tau (Tensor) – A tensor with shape (*, k) where * is zero or more batch dimensions.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, the dtype is same as input tensor, the Q in QR decomposition.

$out = Q = H_1H_2H_3...H_k$

Examples

>>> import paddle
>>> x = paddle.to_tensor([[-1.1280,  0.9012, -0.0190],
...         [ 0.3699,  2.2133, -1.4792],
...         [ 0.0308,  0.3361, -3.1761],
...         [-0.0726,  0.8245, -0.3812]])
>>> tau = paddle.to_tensor([1.7497, 1.1156, 1.7462])
>>> Q = paddle.linalg.householder_product(x, tau)
>>> print(Q)
Tensor(shape=[4, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[-0.74969995, -0.02181768,  0.31115776],
        [-0.64721400, -0.12367040, -0.21738708],
        [-0.05389076, -0.37562513, -0.84836429],
        [ 0.12702821, -0.91822827,  0.36892807]])

hsplit ( num_or_indices: int | Sequence[int], name: str | None = None ) → list[Tensor] [source] hsplit¶

hsplit Full name Horizontal Split, splits the input Tensor into multiple sub-Tensors along the horizontal axis, in the following two cases:

When the dimension of x is equal to 1, it is equivalent to paddle.tensor_split with axis=0;
when the dimension of x is greater than 1, it is equivalent to paddle.tensor_split with axis=1.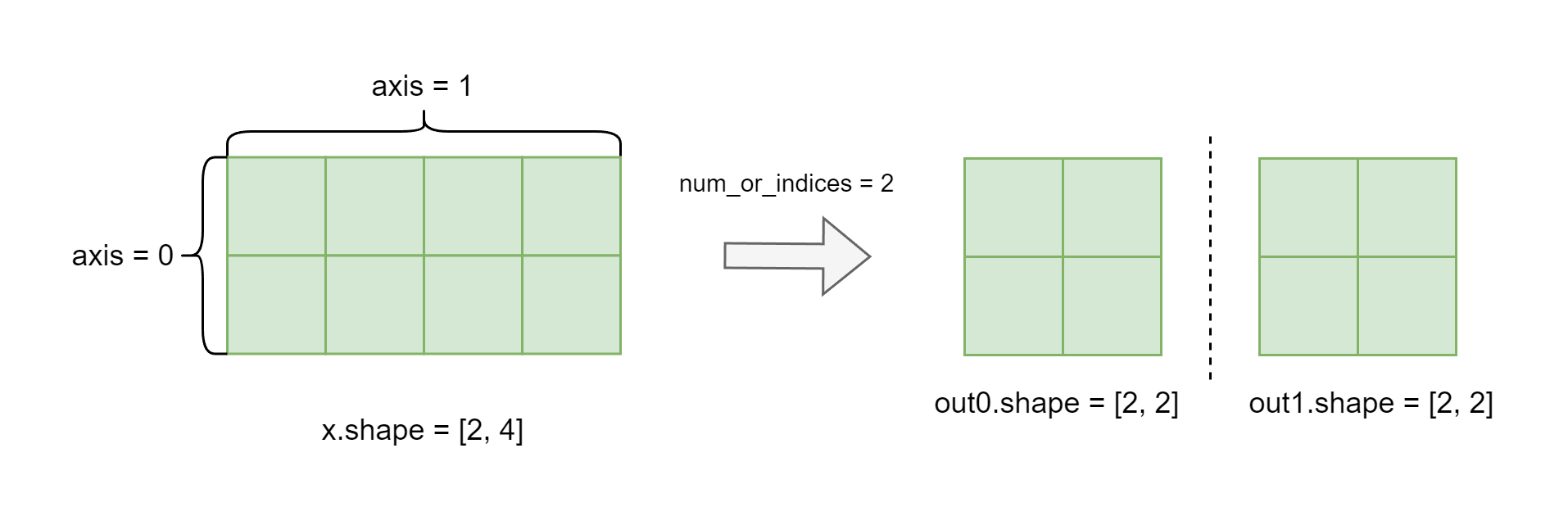

Parameters

x (Tensor) – A Tensor whose dimension must be greater than 0. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If num_or_indices is an int n, x is split into n sections. If num_or_indices is a list or tuple of integer indices, x is split at each of the indices.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

list[Tensor], The list of segmented Tensors.

Examples

>>> import paddle

>>> # x is a Tensor of shape [8]
>>> x = paddle.rand([8])
>>> out0, out1 = paddle.hsplit(x, num_or_indices=2)
>>> print(out0.shape)
[4]
>>> print(out1.shape)
[4]

>>> # x is a Tensor of shape [7, 8]
>>> x = paddle.rand([7, 8])
>>> out0, out1 = paddle.hsplit(x, num_or_indices=2)
>>> print(out0.shape)
[7, 4]
>>> print(out1.shape)
[7, 4]

>>> out0, out1, out2 = paddle.hsplit(x, num_or_indices=[1, 4])
>>> print(out0.shape)
[7, 1]
>>> print(out1.shape)
[7, 3]
>>> print(out2.shape)
[7, 4]

hypot ( y: Tensor, name: str | None = None ) → Tensor [source] hypot¶

Calculate the length of the hypotenuse of a right-angle triangle. The equation is:

\[out = {\sqrt{x^2 + y^2}}\]

Parameters

x (Tensor) – The input Tensor, the data type is float32, float64, int32 or int64.
y (Tensor) – The input Tensor, the data type is float32, float64, int32 or int64.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to Name.

Returns

An N-D Tensor. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y. And the data type is float32 or float64.

Return type

out (Tensor)

Examples

>>> import paddle

>>> x = paddle.to_tensor([3], dtype='float32')
>>> y = paddle.to_tensor([4], dtype='float32')
>>> res = paddle.hypot(x, y)
>>> print(res)
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True,
[5.])

hypot_ ( y: Tensor, name: str | None = None ) → Tensor [source] hypot_¶: Inplace version of hypot API, the output Tensor will be inplaced with input x. Please refer to hypot.

i0 ( name: str | None = None ) → Tensor [source] i0¶

The function used to calculate modified bessel function of order 0.

Equation:: \[I_0(x) = \sum^{\infty}_{k=0}\frac{(x^2/4)^k}{(k!)^2}\]

Parameters

x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

out (Tensor), A Tensor. the value of the modified bessel function of order 0 at x

(integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32")
>>> paddle.i0(x)
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.99999994 , 1.26606596 , 2.27958512 , 4.88079262 , 11.30192089])

i0_ ( name: str | None = None ) → Tensor [source] i0_¶: Inplace version of i0 API, the output Tensor will be inplaced with input x. Please refer to i0.

i0e ( name: str | None = None ) → Tensor [source] i0e¶

The function used to calculate exponentially scaled modified Bessel function of order 0.

Equation:: \[\begin{split}I_0(x) = \sum^{\infty}_{k=0}\frac{(x^2/4)^k}{(k!)^2} \\ I_{0e}(x) = e^{-|x|}I_0(x)\end{split}\]

Parameters

x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

out (Tensor), A Tensor. the value of the exponentially scaled modified Bessel function of order 0 at x

(integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32")
>>> print(paddle.i0e(x))
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.99999994, 0.46575963, 0.30850831, 0.24300036, 0.20700191])

i1 ( name: str | None = None ) → Tensor [source] i1¶

The function is used to calculate modified bessel function of order 1.

Parameters

x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

out (Tensor), A Tensor. the value of the modified bessel function of order 1 at x

(integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32")
>>> print(paddle.i1(x))
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.        , 0.56515908, 1.59063685, 3.95337057, 9.75946712])

i1e ( name: str | None = None ) → Tensor [source] i1e¶

The function is used to calculate exponentially scaled modified Bessel function of order 1.

Parameters

x (Tensor) – The input tensor, it’s data type should be float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

out (Tensor), A Tensor. the value of the exponentially scaled modified Bessel function of order 1 at x

(integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([0, 1, 2, 3, 4], dtype="float32")
>>> print(paddle.i1e(x))
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.        , 0.20791042, 0.21526928, 0.19682673, 0.17875087])

imag ( name: str | None = None ) → Tensor [source] imag¶

Returns a new tensor containing imaginary values of input tensor.

Parameters

x (Tensor) – the input tensor, its data type could be complex64 or complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

a tensor containing imaginary values of the input tensor.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor(
...     [[1 + 6j, 2 + 5j, 3 + 4j], [4 + 3j, 5 + 2j, 6 + 1j]])
>>> print(x)
Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[(1+6j), (2+5j), (3+4j)],
 [(4+3j), (5+2j), (6+1j)]])

>>> imag_res = paddle.imag(x)
>>> print(imag_res)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[6., 5., 4.],
 [3., 2., 1.]])

>>> imag_t = x.imag()
>>> print(imag_t)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[6., 5., 4.],
 [3., 2., 1.]])

increment ( value: float = 1.0, name: str | None = None ) → Tensor [source] increment¶

The API is usually used for control flow to increment the data of x by an amount value. Notice that the number of elements in x must be equal to 1.

Parameters

x (Tensor) – A tensor that must always contain only one element, its data type supports float32, float64, int32 and int64.
value (float, optional) – The amount to increment the data of x. Default: 1.0.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the elementwise-incremented tensor with the same shape and data type as x.

Examples

>>> import paddle

>>> data = paddle.zeros(shape=[1], dtype='float32')
>>> counter = paddle.increment(data)
>>> counter
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.])

index_add ( index: Tensor, axis: int, value: Tensor, name: str | None = None ) → Tensor [source] index_add¶

Adds the elements of the input tensor with value tensor by selecting the indices in the order given in index.

Parameters

x (Tensor) – The Destination Tensor. Supported data types are int32, int64, float16, float32, float64.
index (Tensor) – The 1-D Tensor containing the indices to index. The data type of index must be int32 or int64.
axis (int) – The dimension in which we index.
value (Tensor) – The tensor used to add the elements along the target axis.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, same dimension and dtype with x.

Examples

>>> 
>>> import paddle
>>> paddle.device.set_device('gpu')

>>> input_tensor = paddle.to_tensor(paddle.ones((3, 3)), dtype="float32")
>>> index = paddle.to_tensor([0, 2], dtype="int32")
>>> value = paddle.to_tensor([[1, 1, 1], [1, 1, 1]], dtype="float32")
>>> outplace_res = paddle.index_add(input_tensor, index, 0, value)
>>> print(outplace_res)
Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
[[2., 2., 2.],
 [1., 1., 1.],
 [2., 2., 2.]])

index_add_ ( index: Tensor, axis: int, value: Tensor, name: str | None = None ) → Tensor [source] index_add_¶: Inplace version of index_add API, the output Tensor will be inplaced with input x. Please refer to index_add.

index_fill ( index: Tensor, axis: int, value: float, name: str | None = None ) [source] index_fill¶

Fill the elements of the input tensor with value by the specific axis and index.

As shown below, a [3, 3] 2D tensor is updated via the index_fill operation. With axis=0, index=[0, 2] and value=-1, the 1st and 3rd row elements become -1. The resulting tensor, still [3, 3], has updated values.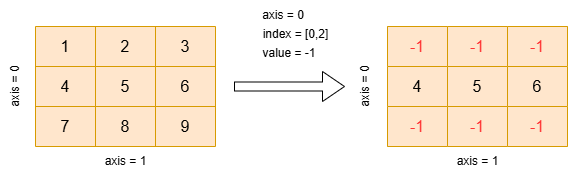

Parameters

x (Tensor) – The Destination Tensor. Supported data types are int32, int64, float16, float32, float64.
index (Tensor) – The 1-D Tensor containing the indices to index. The data type of index must be int32 or int64.
axis (int) – The dimension along which to index.
value (int|float) – The tensor used to fill with.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, same dimension and dtype with x.

Examples

>>> import paddle
>>> input_tensor = paddle.to_tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype='int64')
>>> index = paddle.to_tensor([0, 2], dtype="int32")
>>> value = -1
>>> res = paddle.index_fill(input_tensor, index, 0, value)
>>> print(input_tensor)
Tensor(shape=[3, 3], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])
>>> print(res)
Tensor(shape=[3, 3], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [[-1, -1, -1],
        [ 4,  5,  6],
        [-1, -1, -1]])

index_fill_ ( index: Tensor, axis: int, value: float, name: str | None = None ) [source] index_fill_¶: Inplace version of index_fill API, the output Tensor will be inplaced with input x. Please refer to index_fill.

index_put ( indices: Sequence[Tensor], value: Tensor, accumulate: bool = False, name: str | None = None ) → Tensor [source] index_put¶

Puts values from the tensor values into the tensor x using the indices specified in indices (which is a tuple of Tensors). The expression paddle.index_put_(x, indices, values) is equivalent to tensor[indices] = values. Returns x. If accumulate is True, the elements in values are added to x. If accumulate is False, the behavior is undefined if indices contain duplicate elements.

Parameters

x (Tensor) – The Source Tensor. Supported data types are int32, int64, float16, float32, float64, bool.
indices (list[Tensor]|tuple[Tensor]) – The tuple of Tensor containing the indices to index. The data type of tensor in indices must be int32, int64 or bool.
value (Tensor) – The tensor used to be assigned to x.
accumulate (bool, optional) – Whether the elements in values are added to x. Default: False.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, same dimension and dtype with x.

Examples

>>> import paddle

>>> x = paddle.zeros([3, 3])
>>> value = paddle.ones([3])
>>> ix1 = paddle.to_tensor([0,1,2])
>>> ix2 = paddle.to_tensor([1,2,1])
>>> indices=(ix1,ix2)

>>> out = paddle.index_put(x,indices,value)
>>> print(x)
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 0., 0.],
 [0., 0., 0.],
 [0., 0., 0.]])
>>> print(out)
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 1., 0.],
 [0., 0., 1.],
 [0., 1., 0.]])

index_put_ ( indices: Sequence[Tensor], value: Tensor, accumulate: bool = False, name: str | None = None ) → Tensor [source] index_put_¶: Inplace version of index_put API, the output Tensor will be inplaced with input x. Please refer to index_put.

index_sample ( index: Tensor ) → Tensor [source] index_sample¶

IndexSample Layer

IndexSample OP returns the element of the specified location of X, and the location is specified by Index.

Given:

X = [[1, 2, 3, 4, 5],
     [6, 7, 8, 9, 10]]

Index = [[0, 1, 3],
         [0, 2, 4]]

Then:

Out = [[1, 2, 4],
       [6, 8, 10]]

Parameters

x (Tensor) – The source input tensor with 2-D shape. Supported data type is int32, int64, bfloat16, float16, float32, float64, complex64, complex128.
index (Tensor) – The index input tensor with 2-D shape, first dimension should be same with X. Data type is int32 or int64.

Returns

Tensor, The output is a tensor with the same shape as index.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0, 3.0, 4.0],
...                       [5.0, 6.0, 7.0, 8.0],
...                       [9.0, 10.0, 11.0, 12.0]], dtype='float32')
>>> index = paddle.to_tensor([[0, 1, 2],
...                           [1, 2, 3],
...                           [0, 0, 0]], dtype='int32')
>>> target = paddle.to_tensor([[100, 200, 300, 400],
...                            [500, 600, 700, 800],
...                            [900, 1000, 1100, 1200]], dtype='int32')
>>> out_z1 = paddle.index_sample(x, index)
>>> print(out_z1.numpy())
[[1. 2. 3.]
 [6. 7. 8.]
 [9. 9. 9.]]

>>> # Use the index of the maximum value by topk op
>>> # get the value of the element of the corresponding index in other tensors
>>> top_value, top_index = paddle.topk(x, k=2)
>>> out_z2 = paddle.index_sample(target, top_index)
>>> print(top_value.numpy())
[[ 4.  3.]
 [ 8.  7.]
 [12. 11.]]

>>> print(top_index.numpy())
[[3 2]
 [3 2]
 [3 2]]

>>> print(out_z2.numpy())
[[ 400  300]
 [ 800  700]
 [1200 1100]]

index_select ( index: Tensor, axis: int = 0, name: str | None = None ) → Tensor [source] index_select¶

Returns a new tensor which indexes the input tensor along dimension axis using the entries in index which is a Tensor. The returned tensor has the same number of dimensions as the original x tensor. The dim-th dimension has the same size as the length of index; other dimensions have the same size as in the x tensor.

Parameters

x (Tensor) – The input Tensor to be operated. The data of x can be one of float16, float32, float64, int32, int64, complex64 and complex128.
index (Tensor) – The 1-D Tensor containing the indices to index. The data type of index must be int32 or int64.
axis (int, optional) – The dimension in which we index. Default: if None, the axis is 0.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, A Tensor with same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0, 3.0, 4.0],
...                       [5.0, 6.0, 7.0, 8.0],
...                       [9.0, 10.0, 11.0, 12.0]])
>>> index = paddle.to_tensor([0, 1, 1], dtype='int32')
>>> out_z1 = paddle.index_select(x=x, index=index)
>>> print(out_z1.numpy())
[[1. 2. 3. 4.]
 [5. 6. 7. 8.]
 [5. 6. 7. 8.]]
>>> out_z2 = paddle.index_select(x=x, index=index, axis=1)
>>> print(out_z2.numpy())
[[ 1.  2.  2.]
 [ 5.  6.  6.]
 [ 9. 10. 10.]]

indices ( ) indices¶

Note

This API is only available for SparseCooTensor.

Returns the indices of non zero elements in input SparseCooTensor.

Returns: DenseTensor

Examples

>>> import paddle

>>> indices = [[0, 1, 2], [1, 2, 0]]
>>> values = [1.0, 2.0, 3.0]
>>> dense_shape = [3, 3]
>>> coo = paddle.sparse.sparse_coo_tensor(indices, values, dense_shape)
>>> coo.indices()
Tensor(shape=[2, 3], dtype=int64, place=Place(gpu:0), stop_gradient=True,
[[0, 1, 2],
 [1, 2, 0]])

inner ( y: Tensor, name: str | None = None ) → Tensor [source] inner¶

Inner product of two input Tensor.

Ordinary inner product for 1-D Tensors, in higher dimensions a sum product over the last axes.

Parameters

x (Tensor) – An N-D Tensor or a Scalar Tensor. If its not a scalar Tensor, its last dimensions must match y’s.
y (Tensor) – An N-D Tensor or a Scalar Tensor. If its not a scalar Tensor, its last dimensions must match x’s.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The inner-product Tensor, the output shape is x.shape[:-1] + y.shape[:-1].

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.arange(1, 7).reshape((2, 3)).astype('float32')
>>> y = paddle.arange(1, 10).reshape((3, 3)).astype('float32')
>>> out = paddle.inner(x, y)
>>> print(out)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[14. , 32. , 50. ],
 [32. , 77. , 122.]])

property inplace_version : int

The inplace version of current Tensor. The version number is incremented whenever the current Tensor is modified through an inplace operation.

Notes: This is a read-only property

Examples

>>> import paddle
>>> var = paddle.ones(shape=[4, 2, 3], dtype="float32")
>>> print(var.inplace_version)
0

>>> var[1] = 2.2
>>> print(var.inplace_version)
1

inverse ( name: str | None = None ) → Tensor [source] inverse¶

Takes the inverse of the square matrix. A square matrix is a matrix with the same number of rows and columns. The input can be a square matrix (2-D Tensor) or batches of square matrices.

Parameters

x (Tensor) – The input tensor. The last two dimensions should be equal. When the number of dimensions is greater than 2, it is treated as batches of square matrix. The data type can be float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

A Tensor holds the inverse of x. The shape and data type: is the same as x.

Return type

Tensor

Examples

>>> import paddle

>>> mat = paddle.to_tensor([[2, 0], [0, 2]], dtype='float32')
>>> inv = paddle.inverse(mat)
>>> print(inv)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.50000000, 0.        ],
 [0.        , 0.50000000]])

is_coalesced ( ) is_coalesced¶

Check whether the Tensor is a coalesced SparseCooTensor. If not it will return False. Tensor types other than SparseCooTensor are not supported.

Notes

It will return always False for a newly created SparseCooTensor.

Parameters: x (Tensor) – The input tensor. It can only be SparseCooTensor.
Returns: True if the Tensor is a coalesced SparseCooTensor, and False otherwise.
Return type: bool

Examples

>>> import paddle

>>> indices = [[0, 0, 1], [1, 1, 2]]
>>> values = [1.0, 2.0, 3.0]
>>> x = paddle.sparse.sparse_coo_tensor(indices, values)

>>> x.is_coalesced()
False
>>> x = x.coalesce()
>>> x.is_coalesced()
True

>>> indices = [[0, 1, 1], [1, 0, 2]]
>>> values = [1.0, 2.0, 3.0]
>>> x = paddle.sparse.sparse_coo_tensor(indices, values)
>>> x.is_coalesced()
False

is_complex ( ) → bool [source] is_complex¶

Return whether x is a tensor of complex data type(complex64 or complex128).

Parameters: x (Tensor) – The input tensor.
Returns: True if the data type of the input is complex data type, otherwise false.
Return type: bool

Examples

>>> import paddle

>>> x = paddle.to_tensor([1 + 2j, 3 + 4j])
>>> print(paddle.is_complex(x))
True

>>> x = paddle.to_tensor([1.1, 1.2])
>>> print(paddle.is_complex(x))
False

>>> x = paddle.to_tensor([1, 2, 3])
>>> print(paddle.is_complex(x))
False

is_contiguous ( ) is_contiguous¶

Whether the Tensor is contiguous.

Returns: Bool, Whether the Tensor is contiguous.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = x[1]
>>> print(y.is_contiguous())

is_dense ( ) is_dense¶

Whether the Tensor is a Dense Tensor.

Returns: Whether the Tensor is a Dense Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1.0], stop_gradient=False)
>>> print(x.is_dense())
True

is_dist ( ) is_dist¶

Whether the Tensor is a Distributed Tensor.

Returns: Whether the Tensor is a Distributed Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1.0], stop_gradient=False)
>>> print(x.is_dist())
False

is_empty ( name: str | None = None ) → Tensor [source] is_empty¶

Test whether a Tensor is empty.

Parameters

x (Tensor) – The Tensor to be tested.
name (str|None, optional) – The default value is None . Normally users don’t have to set this parameter. For more information, please refer to Name .

Returns

A bool scalar Tensor. True if ‘x’ is an empty Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> input = paddle.rand(shape=[4, 32, 32], dtype='float32')
>>> res = paddle.is_empty(x=input)
>>> print(res)
Tensor(shape=[], dtype=bool, place=Place(cpu), stop_gradient=True,
False)

is_floating_point ( ) → bool [source] is_floating_point¶

Returns whether the dtype of x is one of paddle.float64, paddle.float32, paddle.float16, and paddle.bfloat16.

Parameters: x (Tensor) – The input tensor.
Returns: True if the dtype of x is floating type, otherwise false.
Return type: bool

Examples

>>> import paddle

>>> x = paddle.arange(1., 5., dtype='float32')
>>> y = paddle.arange(1, 5, dtype='int32')
>>> print(paddle.is_floating_point(x))
True
>>> print(paddle.is_floating_point(y))
False

is_integer ( ) → bool [source] is_integer¶

Return whether x is a tensor of integral data type.

Parameters: x (Tensor) – The input tensor.
Returns: True if the data type of the input is integer data type, otherwise false.
Return type: bool

Examples

>>> import paddle

>>> x = paddle.to_tensor([1 + 2j, 3 + 4j])
>>> print(paddle.is_integer(x))
False

>>> x = paddle.to_tensor([1.1, 1.2])
>>> print(paddle.is_integer(x))
False

>>> x = paddle.to_tensor([1, 2, 3])
>>> print(paddle.is_integer(x))
True

is_leaf

Whether a Tensor is leaf Tensor.

For the Tensor whose stop_gradient is True , it will be leaf Tensor.

For the Tensor whose stop_gradient is False , it will be leaf Tensor too if it is created by user.

Returns: Whether a Tensor is leaf Tensor.
Return type: bool

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.)
>>> print(x.is_leaf)
True

>>> x = paddle.to_tensor(1., stop_gradient=True)
>>> y = x + 1
>>> print(x.is_leaf)
True

>>> print(y.is_leaf)
True

>>> x = paddle.to_tensor(1., stop_gradient=False)
>>> y = x + 1
>>> print(x.is_leaf)
True

>>> print(y.is_leaf)
False

is_same_shape ( y, / ) is_same_shape¶

Return the results of shape comparison between two Tensors, check whether x.shape equal to y.shape. Any two type Tensor among DenseTensor/SparseCooTensor/SparseCsrTensor are supported.

Parameters

x (Tensor) – The input tensor. It can be DenseTensor/SparseCooTensor/SparseCsrTensor.
y (Tensor) – The input tensor. It can be DenseTensor/SparseCooTensor/SparseCsrTensor.

Returns

True for same shape and False for different shape.

Return type

bool

Examples

>>> import paddle

>>> x = paddle.rand([2, 3, 8])
>>> y = paddle.rand([2, 3, 8])
>>> y = y.to_sparse_csr()
>>> z = paddle.rand([2, 5])

>>> x.is_same_shape(y)
True
>>> x.is_same_shape(z)
False

is_sparse ( ) is_sparse¶

Returns whether the input Tensor is SparseCooTensor or SparseCsrTensor.

When input is SparseCooTensor/SparseCsrTensor, will return True. When input is DenseTensor, will return False.

Returns: bool

Examples

>>> import paddle

>>> indices = [[0, 1, 2], [1, 2, 0]]
>>> values = [1.0, 2.0, 3.0]
>>> dense_shape = [3, 3]
>>> coo = paddle.sparse.sparse_coo_tensor(indices, values, dense_shape)
>>> coo.is_sparse()
True

is_sparse_coo ( ) is_sparse_coo¶

Returns whether the input Tensor is SparseCooTensor.

When input is SparseCooTensor, will return True. When input is DenseTensor/SparseCsrTensor, will return False.

Returns: bool

Examples

>>> import paddle

>>> indices = [[0, 1, 2], [1, 2, 0]]
>>> values = [1.0, 2.0, 3.0]
>>> dense_shape = [3, 3]
>>> coo = paddle.sparse.sparse_coo_tensor(indices, values, dense_shape)
>>> coo.is_sparse_coo()
True

is_sparse_csr ( ) is_sparse_csr¶

Returns whether the input Tensor is SparseCsrTensor.

When input is SparseCsrTensor, will return True. When input is DenseTensor/SparseCooTensor, will return False.

Returns: bool

Examples

>>> import paddle

>>> crows = [0, 2, 3, 5]
>>> cols = [1, 3, 2, 0, 1]
>>> values = [1, 2, 3, 4, 5]
>>> dense_shape = [3, 4]
>>> csr = paddle.sparse.sparse_csr_tensor(crows, cols, values, dense_shape)
>>> csr.is_sparse_csr()
True

is_tensor ( ) → TypeGuard[Tensor] [source] is_tensor¶

Tests whether input object is a paddle.Tensor.

Parameters: x (object) – Object to test.
Returns: A boolean value. True if x is a paddle.Tensor, otherwise False.

Examples

>>> import paddle

>>> input1 = paddle.rand(shape=[2, 3, 5], dtype='float32')
>>> check = paddle.is_tensor(input1)
>>> print(check)
True

>>> input3 = [1, 4]
>>> check = paddle.is_tensor(input3)
>>> print(check)
False

isclose ( y: Tensor, rtol: float = 1e-05, atol: float = 1e-08, equal_nan: bool = False, name: str | None = None ) → Tensor [source] isclose¶

Check if all $x$ and $y$ satisfy the condition:

\[\left| x - y \right| \leq atol + rtol \times \left| y \right|\]

elementwise, for all elements of $x$ and $y$. The behaviour of this operator is analogous to $numpy.isclose$, namely that it returns $True$ if two tensors are elementwise equal within a tolerance.

Parameters

x (Tensor) – The input tensor, it’s data type should be float16, float32, float64, complex64, complex128.
y (Tensor) – The input tensor, it’s data type should be float16, float32, float64, complex64, complex128.
rtol (float, optional) – The relative tolerance. Default: $1e-5$ .
atol (float, optional) – The absolute tolerance. Default: $1e-8$ .
equal_nan (bool, optional) – If $True$ , then two $NaNs$ will be compared as equal. Default: $False$ .
name (str|None, optional) – Name for the operation. For more information, please refer to Name. Default: None.

Returns

The output tensor, it’s data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([10000., 1e-07])
>>> y = paddle.to_tensor([10000.1, 1e-08])
>>> result1 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08,
...                          equal_nan=False, name="ignore_nan")
>>> print(result1)
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False])
>>> result2 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08,
...                          equal_nan=True, name="equal_nan")
>>> print(result2)
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False])
>>> x = paddle.to_tensor([1.0, float('nan')])
>>> y = paddle.to_tensor([1.0, float('nan')])
>>> result1 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08,
...                          equal_nan=False, name="ignore_nan")
>>> print(result1)
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False])
>>> result2 = paddle.isclose(x, y, rtol=1e-05, atol=1e-08,
...                          equal_nan=True, name="equal_nan")
>>> print(result2)
Tensor(shape=[2], dtype=bool, place=Place(cpu), stop_gradient=True,
[True, True])

isfinite ( name: str | None = None ) → Tensor [source] isfinite¶

Return whether every element of input tensor is finite number or not.

Parameters

x (Tensor) – The input tensor, it’s data type should be float16, float32, float64, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the bool result which shows every element of x whether it is finite number or not.

Examples

>>> import paddle

>>> x = paddle.to_tensor([float('-inf'), -2, 3.6, float('inf'), 0, float('-nan'), float('nan')])
>>> out = paddle.isfinite(x)
>>> out
Tensor(shape=[7], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True , True , False, True , False, False])

isin ( test_x: Tensor, assume_unique: bool = False, invert: bool = False, name: str | None = None ) → Tensor [source] isin¶

Tests if each element of x is in test_x.

Parameters

x (Tensor) – The input Tensor. Supported data type: ‘bfloat16’, ‘float16’, ‘float32’, ‘float64’, ‘int32’, ‘int64’.
test_x (Tensor) – Tensor values against which to test for each input element. Supported data type: ‘bfloat16’, ‘float16’, ‘float32’, ‘float64’, ‘int32’, ‘int64’.
assume_unique (bool, optional) – If True, indicates both x and test_x contain unique elements, which could make the calculation faster. Default: False.
invert (bool, optional) – Indicate whether to invert the boolean return tensor. If True, invert the results. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to Name.

Returns

out (Tensor), The output Tensor with the same shape as x.

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> x = paddle.to_tensor([-0., -2.1, 2.5, 1.0, -2.1], dtype='float32')
>>> test_x = paddle.to_tensor([-2.1, 2.5], dtype='float32')
>>> res = paddle.isin(x, test_x)
>>> print(res)
Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True, True, False, True])

>>> x = paddle.to_tensor([-0., -2.1, 2.5, 1.0, -2.1], dtype='float32')
>>> test_x = paddle.to_tensor([-2.1, 2.5], dtype='float32')
>>> res = paddle.isin(x, test_x, invert=True)
>>> print(res)
Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True,
[True, False, False, True, False])

>>> # Set `assume_unique` to True only when `x` and `test_x` contain unique values, otherwise the result may be incorrect.
>>> x = paddle.to_tensor([0., 1., 2.]*20).reshape([20, 3])
>>> test_x = paddle.to_tensor([0., 1.]*20)
>>> correct_result = paddle.isin(x, test_x, assume_unique=False)
>>> print(correct_result)
Tensor(shape=[20, 3], dtype=bool, place=Place(cpu), stop_gradient=True,
[[True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False],
 [True , True , False]])

>>> incorrect_result = paddle.isin(x, test_x, assume_unique=True)
>>> print(incorrect_result)
Tensor(shape=[20, 3], dtype=bool, place=Place(gpu:0), stop_gradient=True,
[[True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , True ],
 [True , True , False]])

isinf ( name: str | None = None ) → Tensor [source] isinf¶

Return whether every element of input tensor is +/-INF or not.

Parameters

x (Tensor) – The input tensor, it’s data type should be float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the bool result which shows every element of x whether it is +/-INF or not.

Examples

>>> import paddle

>>> x = paddle.to_tensor([float('-inf'), -2, 3.6, float('inf'), 0, float('-nan'), float('nan')])
>>> out = paddle.isinf(x)
>>> out
Tensor(shape=[7], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False, False, True , False, False, False])

isnan ( name: str | None = None ) → Tensor [source] isnan¶

Return whether every element of input tensor is NaN or not.

Parameters

x (Tensor) – The input tensor, it’s data type should be float16, float32, float64, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the bool result which shows every element of x whether it is NaN or not.

Examples

>>> import paddle

>>> x = paddle.to_tensor([float('-inf'), -2, 3.6, float('inf'), 0, float('-nan'), float('nan')])
>>> out = paddle.isnan(x)
>>> out
Tensor(shape=[7], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, False, False, False, False, True , True ])

isneginf ( name: str | None = None ) → Tensor [source] isneginf¶

Tests if each element of input is negative infinity or not.

Parameters

x (Tensor) – The input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), The output Tensor. Each element of output indicates whether the input element is negative infinity or not.

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> x = paddle.to_tensor([-0., float('inf'), -2.1, -float('inf'), 2.5], dtype='float32')
>>> res = paddle.isneginf(x)
>>> print(res)
Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, False, False, True, False])

isposinf ( name: str | None = None ) → Tensor [source] isposinf¶

Tests if each element of input is positive infinity or not.

Parameters

x (Tensor) – The input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), The output Tensor. Each element of output indicates whether the input element is positive infinity or not.

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> x = paddle.to_tensor([-0., float('inf'), -2.1, -float('inf'), 2.5], dtype='float32')
>>> res = paddle.isposinf(x)
>>> print(res)
Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True, False, False, False])

isreal ( name: str | None = None ) → Tensor [source] isreal¶

Tests if each element of input is a real number or not.

Parameters

x (Tensor) – The input Tensor.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), The output Tensor. Each element of output indicates whether the input element is a real number or not.

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> x = paddle.to_tensor([-0., -2.1, 2.5], dtype='float32')
>>> res = paddle.isreal(x)
>>> print(res)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[True, True, True])

>>> x = paddle.to_tensor([(-0.+1j), (-2.1+0.2j), (2.5-3.1j)])
>>> res = paddle.isreal(x)
>>> print(res)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, False, False])

>>> x = paddle.to_tensor([(-0.+1j), (-2.1+0j), (2.5-0j)])
>>> res = paddle.isreal(x)
>>> print(res)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True, True])

istft ( n_fft: int, hop_length: int | None = None, win_length: int | None = None, window: Tensor | None = None, center: bool = True, normalized: bool = False, onesided: bool = True, length: int | None = None, return_complex: bool = False, name: str | None = None ) → Tensor istft¶

Inverse short-time Fourier transform (ISTFT).

Reconstruct time-domain signal from the giving complex input and window tensor when nonzero overlap-add (NOLA) condition is met:

\[\sum_{t = -\infty}^{\infty} \text{window}^2[n - t \times H]\ \neq \ 0, \ \text{for } all \ n\]

Where: - $t$: The $t$-th input window. - $N$: Value of n_fft. - $H$: Value of hop_length.

Result of istft expected to be the inverse of paddle.signal.stft, but it is not guaranteed to reconstruct a exactly realizable time-domain signal from a STFT complex tensor which has been modified (via masking or otherwise). Therefore, istft gives the [Griffin-Lim optimal estimate] (optimal in a least-squares sense) for the corresponding signal.

Parameters

x (Tensor) – The input data which is a 2-dimensional or 3-dimensional complex Tensor with shape […, n_fft, num_frames].
n_fft (int) – The size of Fourier transform.
hop_length (int|None, optional) – Number of steps to advance between adjacent windows from time-domain signal and 0 < hop_length < win_length. Default: None ( treated as equal to n_fft//4)
win_length (int|None, optional) – The size of window. Default: None (treated as equal to n_fft)
window (Tensor|None, optional) – A 1-dimensional tensor of size win_length. It will be center padded to length n_fft if win_length < n_fft. It should be a real-valued tensor if return_complex is False. Default: None`(treated as a rectangle window with value equal to 1 of size `win_length).
center (bool, optional) – It means that whether the time-domain signal has been center padded. Default: True.
normalized (bool, optional) – Control whether to scale the output by $1/sqrt(n_{fft})$. Default: False
onesided (bool, optional) – It means that whether the input STFT tensor is a half of the conjugate symmetry STFT tensor transformed from a real-valued signal and istft will return a real-valued tensor when it is set to True. Default: True.
length (int|None, optional) – Specify the length of time-domain signal. Default: `None`( treated as the whole length of signal).
return_complex (bool, optional) – It means that whether the time-domain signal is real-valued. If return_complex is set to True, onesided should be set to False cause the output is complex.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

A tensor of least squares estimation of the reconstructed signal(s) with shape […, seq_length]

Examples

>>> import numpy as np
>>> import paddle
>>> from paddle.signal import stft, istft

>>> paddle.seed(0)

>>> # STFT
>>> x = paddle.randn([8, 48000], dtype=paddle.float64)
>>> y = stft(x, n_fft=512)
>>> print(y.shape)
[8, 257, 376]

>>> # ISTFT
>>> x_ = istft(y, n_fft=512)
>>> print(x_.shape)
[8, 48000]

>>> np.allclose(x, x_)
True

item ( *args: int ) → float | bool | complex item¶

Convert element at specific position in Tensor into Python scalars. If the position is not specified, the Tensor must be a single-element Tensor.

Parameters: *args (int) – The input coordinates. If it’s single int, the data in the corresponding order of flattened Tensor will be returned. Default: None, and it must be in the case where Tensor has only one element.

Returns(Python scalar): A Python scalar, whose dtype is corresponds to the dtype of Tensor.

Raises: ValueError – If the Tensor has more than one element, there must be coordinates.

Examples

>>> import paddle

>>> x = paddle.to_tensor(1)
>>> print(x.item())
1
>>> print(type(x.item()))
<class 'int'>

>>> x = paddle.to_tensor(1.0)
>>> print(x.item())
1.0
>>> print(type(x.item()))
<class 'float'>

>>> x = paddle.to_tensor(True)
>>> print(x.item())
True
>>> print(type(x.item()))
<class 'bool'>

>>> x = paddle.to_tensor(1+1j)
>>> print(x.item())
(1+1j)
>>> print(type(x.item()))
<class 'complex'>

>>> x = paddle.to_tensor([[1.1, 2.2, 3.3]])
>>> print(x.item(2))
3.299999952316284
>>> print(x.item(0, 2))
3.299999952316284

kron ( y: Tensor, name: str | None = None ) → Tensor [source] kron¶

Compute the Kronecker product of two tensors, a composite tensor made of blocks of the second tensor scaled by the first. Assume that the rank of the two tensors, $X$ and $Y$ are the same, if necessary prepending the smallest with ones. If the shape of $X$ is [$r_0$, $r_1$, …, $r_N$] and the shape of $Y$ is [$s_0$, $s_1$, …, $s_N$], then the shape of the output tensor is [$r_{0}s_{0}$, $r_{1}s_{1}$, …, $r_{N}s_{N}$]. The elements are products of elements from $X$ and $Y$. The equation is: $$ output[k_{0}, k_{1}, …, k_{N}] = X[i_{0}, i_{1}, …, i_{N}] * Y[j_{0}, j_{1}, …, j_{N}] $$ where $$ k_{t} = i_{t} * s_{t} + j_{t}, t = 0, 1, …, N $$

Parameters

x (Tensor) – the fist operand of kron op, data type: bfloat16, float16, float32, float64, int32 or int64.
y (Tensor) – the second operand of kron op, data type: bfloat16, float16, float32, float64, int32 or int64. Its data type should be the same with x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output of kron, data type: bfloat16, float16, float32, float64, int32 or int64. Its data is the same with x.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([[1, 2], [3, 4]], dtype='int64')
>>> y = paddle.to_tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype='int64')
>>> out = paddle.kron(x, y)
>>> out
Tensor(shape=[6, 6], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 , 2 , 4 , 6 ],
 [4 , 5 , 6 , 8 , 10, 12],
 [7 , 8 , 9 , 14, 16, 18],
 [3 , 6 , 9 , 4 , 8 , 12],
 [12, 15, 18, 16, 20, 24],
 [21, 24, 27, 28, 32, 36]])

kthvalue ( k: int, axis: int | None = None, keepdim: bool = False, name: str | None = None ) → tuple[Tensor, Tensor] [source] kthvalue¶

Find values and indices of the k-th smallest at the axis.

Parameters

x (Tensor) – A N-D Tensor with type float16, float32, float64, int32, int64.
k (int) – The k for the k-th smallest number to look for along the axis.
axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. The default is None. And if the axis is None, it will computed as -1 by default.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
name (str, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

tuple(Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.

Examples

>>> import paddle

>>> x = paddle.randn((2,3,2))
>>> print(x)
>>> 
Tensor(shape=[2, 3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[ 0.11855337, -0.30557564],
  [-0.09968963,  0.41220093],
  [ 1.24004936,  1.50014710]],
 [[ 0.08612321, -0.92485696],
  [-0.09276631,  1.15149164],
  [-1.46587241,  1.22873247]]])
>>> 
>>> y = paddle.kthvalue(x, 2, 1)
>>> print(y)
>>> 
(Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 0.11855337,  0.41220093],
 [-0.09276631,  1.15149164]]), Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 1],
 [1, 1]]))
>>> 

layout

Tensor’s memory layout.

Returns: layout.
Return type: Layout

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> print(x.layout)
NCHW

lcm ( y: Tensor, name: str | None = None ) → Tensor [source] lcm¶

Computes the element-wise least common multiple (LCM) of input |x| and |y|. Both x and y must have integer types.

Note

lcm(0,0)=0, lcm(0, y)=0

If x.shape != y.shape, they must be broadcastable to a common shape (which becomes the shape of the output).

Parameters

x (Tensor) – An N-D Tensor, the data type is int32, int64.
y (Tensor) – An N-D Tensor, the data type is int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor, the data type is the same with input.

Return type

out (Tensor)

Examples

>>> import paddle

>>> x1 = paddle.to_tensor(12)
>>> x2 = paddle.to_tensor(20)
>>> paddle.lcm(x1, x2)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
60)

>>> x3 = paddle.arange(6)
>>> paddle.lcm(x3, x2)
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 20, 20, 60, 20, 20])

>>> x4 = paddle.to_tensor(0)
>>> paddle.lcm(x4, x2)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
0)

>>> paddle.lcm(x4, x4)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
0)

>>> x5 = paddle.to_tensor(-20)
>>> paddle.lcm(x1, x5)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
60)

lcm_ ( y: Tensor, name: str | None = None ) → Tensor [source] lcm_¶: Inplace version of lcm API, the output Tensor will be inplaced with input x. Please refer to lcm.

ldexp ( y: Tensor, name: str | None = None ) → Tensor [source] ldexp¶

Compute the result of multiplying x by 2 to the power of y. The equation is:

\[out = x * 2^{y}\]

Parameters

x (Tensor) – The input Tensor, the data type is float32, float64, int32 or int64.
y (Tensor) – A Tensor of exponents, typically integers.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to Name.

Returns

An N-D Tensor. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y. And the data type is float32 or float64.

Return type

out (Tensor)

Examples

>>> import paddle

>>> # example1
>>> x = paddle.to_tensor([1, 2, 3], dtype='float32')
>>> y = paddle.to_tensor([2, 3, 4], dtype='int32')
>>> res = paddle.ldexp(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[4. , 16., 48.])

>>> # example2
>>> x = paddle.to_tensor([1, 2, 3], dtype='float32')
>>> y = paddle.to_tensor([2], dtype='int32')
>>> res = paddle.ldexp(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[4. , 8. , 12.])

ldexp_ ( y: Tensor, name: str | None = None ) → Tensor [source] ldexp_¶: Inplace version of polygamma API, the output Tensor will be inplaced with input x. Please refer to polygamma.

lerp ( y: Tensor, weight: float | Tensor, name: str | None = None ) → Tensor [source] lerp¶

Does a linear interpolation between x and y based on weight.

Equation:: \[lerp(x, y, weight) = x + weight * (y - x).\]

Parameters

x (Tensor) – An N-D Tensor with starting points, the data type is bfloat16, float16, float32, float64.
y (Tensor) – An N-D Tensor with ending points, the data type is bfloat16, float16, float32, float64.
weight (float|Tensor) – The weight for the interpolation formula. When weight is Tensor, the data type is bfloat16, float16, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor, the shape and data type is the same with input.

Return type

out (Tensor)

Example

>>> import paddle

>>> x = paddle.arange(1., 5., dtype='float32')
>>> y = paddle.empty([4], dtype='float32')
>>> y.fill_(10.)
>>> out = paddle.lerp(x, y, 0.5)
>>> out
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[5.50000000, 6.        , 6.50000000, 7.        ])

lerp_ ( y: Tensor, weight: float | Tensor, name: str | None = None ) → Tensor lerp_¶: Inplace version of lerp API, the output Tensor will be inplaced with input x. Please refer to lerp.

less ( y: Tensor, name: str | None = None ) → Tensor [source] less¶

Returns the truth value of $x < y$ elementwise, which is equivalent function to the overloaded operator <.

Note

The output has no gradient.

Parameters

x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The output shape is same as input x. The output data type is bool.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 3, 2])
>>> result1 = paddle.less(x, y)
>>> print(result1)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True , False])

less_ ( y: Tensor, name: str | None = None ) → Tensor [source] less_¶: Inplace version of less_ API, the output Tensor will be inplaced with input x. Please refer to less.

less_equal ( y: Tensor, name: str | None = None ) → Tensor [source] less_equal¶

Returns the truth value of $x <= y$ elementwise, which is equivalent function to the overloaded operator <=.

Note

The output has no gradient.

Parameters

x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The output shape is same as input x. The output data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 3, 2])
>>> result1 = paddle.less_equal(x, y)
>>> print(result1)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , True , False])

less_equal_ ( y: Tensor, name: str | None = None ) → Tensor [source] less_equal_¶: Inplace version of less_equal API, the output Tensor will be inplaced with input x. Please refer to less_equal.

less_than ( y: Tensor, name: str | None = None ) → Tensor [source] less_than¶

Returns the truth value of $x < y$ elementwise, which is equivalent function to the overloaded operator <.

Note

The output has no gradient.

Parameters

x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The output shape is same as input x. The output data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 3, 2])
>>> result1 = paddle.less_than(x, y)
>>> print(result1)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True , False])

less_than_ ( y: Tensor, name: str | None = None ) → Tensor [source] less_than_¶: Inplace version of less_than API, the output Tensor will be inplaced with input x. Please refer to less_than.

lgamma ( name: str | None = None ) → Tensor [source] lgamma¶

Calculates the lgamma of the given input tensor, element-wise.

This operator performs elementwise lgamma for input $X$. $out = log\Gamma(x)$

Parameters

x (Tensor) – Input Tensor. Must be one of the following types: bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the lgamma of the input Tensor, the shape and data type is the same with input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.lgamma(x)
>>> out
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.31452453, 1.76149762, 2.25271273, 1.09579790])

lgamma_ ( name: str | None = None ) → Tensor [source] lgamma_¶: Inplace version of lgamma API, the output Tensor will be inplaced with input x. Please refer to lgamma.

log ( name: str | None = None ) → Tensor [source] log¶

Calculates the natural log of the given input Tensor, element-wise.

\[Out = \ln(x)\]

Parameters

x (Tensor) – Input Tensor. Must be one of the following types: int32, int64, float16, bfloat16, float32, float64, complex64, complex128.
name (str|None) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name

Returns

The natural log of the input Tensor computed element-wise.

Return type

Tensor

Examples

>>> import paddle

>>> x = [[2, 3, 4], [7, 8, 9]]
>>> x = paddle.to_tensor(x, dtype='float32')
>>> print(paddle.log(x))
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.69314718, 1.09861231, 1.38629436],
 [1.94591010, 2.07944155, 2.19722462]])

log10 ( name: str | None = None ) → Tensor [source] log10¶

Calculates the log to the base 10 of the given input tensor, element-wise.

\[Out = \log_10_x\]

Parameters

x (Tensor) – Input tensor must be one of the following types: int32, int64, float16, bfloat16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The log to the base 10 of the input Tensor computed element-wise.

Return type

Tensor

Examples

>>> import paddle

>>> # example 1: x is a float
>>> x_i = paddle.to_tensor([[1.0], [10.0]])
>>> res = paddle.log10(x_i)
>>> res
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.],
 [1.]])

>>> # example 2: x is float32
>>> x_i = paddle.full(shape=[1], fill_value=10, dtype='float32')
>>> paddle.to_tensor(x_i)
>>> res = paddle.log10(x_i)
>>> res
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.])

>>> # example 3: x is float64
>>> x_i = paddle.full(shape=[1], fill_value=10, dtype='float64')
>>> paddle.to_tensor(x_i)
>>> res = paddle.log10(x_i)
>>> res
Tensor(shape=[1], dtype=float64, place=Place(cpu), stop_gradient=True,
[1.])

log10_ ( name: str | None = None ) → Tensor [source] log10_¶: Inplace version of log10 API, the output Tensor will be inplaced with input x. Please refer to log10.

log1p ( name: str | None = None ) → Tensor [source] log1p¶

Calculates the natural log of the given input tensor, element-wise.

\[Out = \ln(x+1)\]

Parameters

x (Tensor) – Input Tensor. Must be one of the following types: int32, int64, float16, bfloat16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the natural log of the input Tensor computed element-wise.

Examples

>>> import paddle

>>> data = paddle.to_tensor([[0], [1]], dtype='float32')
>>> res = paddle.log1p(data)
>>> res
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.        ],
 [0.69314718]])

log1p_ ( name: str | None = None ) → None [source] log1p_¶: Inplace version of log1p API, the output Tensor will be inplaced with input x. Please refer to log1p.

log2 ( name: str | None = None ) → Tensor [source] log2¶

Calculates the log to the base 2 of the given input tensor, element-wise.

\[Out = \log_2x\]

Parameters

x (Tensor) – Input tensor must be one of the following types: int32, int64, float16, bfloat16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The log to the base 2 of the input Tensor computed element-wise.

Return type

Tensor

Examples

>>> import paddle

>>> # example 1: x is a float
>>> x_i = paddle.to_tensor([[1.0], [2.0]])
>>> res = paddle.log2(x_i)
>>> res
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.],
 [1.]])

>>> # example 2: x is float32
>>> x_i = paddle.full(shape=[1], fill_value=2, dtype='float32')
>>> paddle.to_tensor(x_i)
>>> res = paddle.log2(x_i)
>>> res
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.])

>>> # example 3: x is float64
>>> x_i = paddle.full(shape=[1], fill_value=2, dtype='float64')
>>> paddle.to_tensor(x_i)
>>> res = paddle.log2(x_i)
>>> res
Tensor(shape=[1], dtype=float64, place=Place(cpu), stop_gradient=True,
[1.])

log2_ ( name: str | None = None ) → Tensor [source] log2_¶: Inplace version of log2 API, the output Tensor will be inplaced with input x. Please refer to log2.

log_ ( name: str | None = None ) → Tensor [source] log_¶: Inplace version of log API, the output Tensor will be inplaced with input x. Please refer to log.

log_normal_ ( mean: float = 1.0, std: float = 2.0, name: str | None = None ) → Tensor [source] log_normal_¶

This inplace version of api log_normal, which returns a Tensor filled with random values sampled from a log normal distribution. The output Tensor will be inplaced with input x. Please refer to log_normal.

Parameters

x (Tensor) – The input tensor to be filled with random values.
mean (float|int, optional) – Mean of the output tensor, default is 1.0.
std (float|int, optional) – Standard deviation of the output tensor, default is 2.0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, A Tensor filled with random values sampled from a log normal distribution with the underlying normal distribution’s mean and std .

Examples

>>> import paddle
>>> paddle.seed(200)
>>> x = paddle.randn([3, 4])
>>> x.log_normal_()
>>> print(x)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[3.99360156 , 0.11746082 , 12.14813519, 4.74383831 ],
 [0.36592522 , 0.09426476 , 31.81549835, 0.61839998 ],
 [1.33314908 , 12.31954002, 36.44527435, 1.69572163 ]])

logaddexp ( y: Tensor, name: str | None = None ) → Tensor [source] logaddexp¶

Elementwise LogAddExp Operator. Add of exponentiations of the inputs The equation is:

\[Out=log(X.exp()+Y.exp())\]

$X$ the tensor of any dimension. $Y$ the tensor whose dimensions must be less than or equal to the dimensions of $X$.

There are two cases for this operator:

The shape of $Y$ is the same with $X$.
The shape of $Y$ is a continuous subsequence of $X$.

For case 2:

Broadcast $Y$ to match the shape of $X$, where axis is the start dimension index for broadcasting $Y$ onto $X$.
If $axis$ is -1 (default), $axis$=rank($X$)-rank($Y$).

The trailing dimensions of size 1 for $Y$ will be ignored for the consideration of subsequence, such as shape($Y$) = (2, 1) => (2).

For example:

shape(X) = (2, 3, 4, 5), shape(Y) = (,)
shape(X) = (2, 3, 4, 5), shape(Y) = (5,)
shape(X) = (2, 3, 4, 5), shape(Y) = (4, 5), with axis=-1(default) or axis=2
shape(X) = (2, 3, 4, 5), shape(Y) = (3, 4), with axis=1
shape(X) = (2, 3, 4, 5), shape(Y) = (2), with axis=0
shape(X) = (2, 3, 4, 5), shape(Y) = (2, 1), with axis=0

Parameters

x (Tensor) – Tensor of any dimensions. Its dtype should be int32, int64, bfloat16, float16, float32, float64.
y (Tensor) – Tensor of any dimensions. Its dtype should be int32, int64, bfloat16, float16, float32, float64.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

N-D Tensor. A location into which the result is stored. It’s dimension equals with x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([-1, -2, -3], 'float64')
>>> y = paddle.to_tensor([-1], 'float64')
>>> z = paddle.logaddexp(x, y)
>>> print(z)
Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True,
[-0.30685282, -0.68673831, -0.87307199])

logcumsumexp ( axis: int | None = None, dtype: DTypeLike | None = None, name: str | None = None ) → Tensor [source] logcumsumexp¶

The logarithm of the cumulative summation of the exponentiation of the elements along a given axis.

For summation index j given by axis and other indices i, the result is

\[logcumsumexp(x)_{ij} = log \sum_{i=0}^{j}exp(x_{ij})\]

Note

The first element of the result is the same as the first element of the input.

Parameters

x (Tensor) – The input tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64
axis (int, optional) – The dimension to do the operation along. -1 means the last dimension. The default (None) is to compute the cumsum over the flattened array.
dtype (str|paddle.dtype|np.dtype, optional) – The data type of the output tensor, can be float16, float32, float64. If specified, the input tensor is casted to dtype before the operation is performed. This is useful for preventing data type overflows. The default value is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the result of logcumsumexp operator (integer input types are autocasted into float32).

Examples

>>> import paddle

>>> data = paddle.arange(12, dtype='float64')
>>> data = paddle.reshape(data, (3, 4))

>>> y = paddle.logcumsumexp(data)
>>> y
Tensor(shape=[12], dtype=float64, place=Place(cpu), stop_gradient=True,
[0.         , 1.31326169 , 2.40760596 , 3.44018970 , 4.45191440 ,
 5.45619332 , 6.45776285 , 7.45833963 , 8.45855173 , 9.45862974 ,
 10.45865844, 11.45866900])

>>> y = paddle.logcumsumexp(data, axis=0)
>>> y
Tensor(shape=[3, 4], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0.         , 1.         , 2.         , 3.         ],
 [4.01814993 , 5.01814993 , 6.01814993 , 7.01814993 ],
 [8.01847930 , 9.01847930 , 10.01847930, 11.01847930]])

>>> y = paddle.logcumsumexp(data, axis=-1)
>>> y
Tensor(shape=[3, 4], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0.         , 1.31326169 , 2.40760596 , 3.44018970 ],
 [4.         , 5.31326169 , 6.40760596 , 7.44018970 ],
 [8.         , 9.31326169 , 10.40760596, 11.44018970]])

>>> y = paddle.logcumsumexp(data, dtype='float64')
>>> assert y.dtype == paddle.float64

logical_and ( y: Tensor, out: Tensor | None = None, name: str | None = None ) → Tensor [source] logical_and¶

Compute element-wise logical AND on x and y, and return out. out is N-dim boolean Tensor. Each element of out is calculated by

\[out = x \&\& y\]

Note

paddle.logical_and supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be one of bool, int8, int16, in32, in64, bfloat16, float16, float32, float64, complex64, complex128.
y (Tensor) – the input tensor, it’s data type should be one of bool, int8, int16, in32, in64, bfloat16, float16, float32, float64, complex64, complex128.
out (Tensor|None, optional) – The Tensor that specifies the output of the operator, which can be any Tensor that has been created in the program. The default value is None, and a new Tensor will be created to save the output.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. It’s dimension equals with x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([True])
>>> y = paddle.to_tensor([True, False, True, False])
>>> res = paddle.logical_and(x, y)
>>> print(res)
Tensor(shape=[4], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , False, True , False])

logical_and_ ( y: Tensor, name: str | None = None ) → Tensor [source] logical_and_¶: Inplace version of logical_and API, the output Tensor will be inplaced with input x. Please refer to logical_and.

logical_not ( out: Tensor | None = None, name: str | None = None ) → Tensor [source] logical_not¶

logical_not operator computes element-wise logical NOT on x, and returns out. out is N-dim boolean Variable. Each element of out is calculated by

\[out = !x\]

Note

paddle.logical_not supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – Operand of logical_not operator. Must be a Tensor of type bool, int8, int16, in32, in64, bfloat16, float16, float32, or float64, complex64, complex128.
out (Tensor|None) – The Tensor that specifies the output of the operator, which can be any Tensor that has been created in the program. The default value is None, and a new ``Tensor` will be created to save the output.
name (str|None, optional) – The default value is None. Normally there is no need for users to set this property. For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. It’s dimension equals with x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([True, False, True, False])
>>> res = paddle.logical_not(x)
>>> print(res)
Tensor(shape=[4], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True , False, True ])

logical_not_ ( name: str | None = None ) → Tensor [source] logical_not_¶: Inplace version of logical_not API, the output Tensor will be inplaced with input x. Please refer to logical_not.

logical_or ( y: Tensor, out: Tensor | None = None, name: str | None = None ) → Tensor [source] logical_or¶

logical_or operator computes element-wise logical OR on x and y, and returns out. out is N-dim boolean Tensor. Each element of out is calculated by

\[out = x || y\]

Note

paddle.logical_or supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be one of bool, int8, int16, in32, in64, bfloat16, float16, float32, float64, complex64, complex128.
y (Tensor) – the input tensor, it’s data type should be one of bool, int8, int16, in32, in64, bfloat16, float16, float32, float64, complex64, complex128.
out (Tensor|None, optional) – The Variable that specifies the output of the operator, which can be any Tensor that has been created in the program. The default value is None, and a new Tensor will be created to save the output.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. It’s dimension equals with x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([True, False], dtype="bool").reshape([2, 1])
>>> y = paddle.to_tensor([True, False, True, False], dtype="bool").reshape([2, 2])
>>> res = paddle.logical_or(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=bool, place=Place(cpu), stop_gradient=True,
[[True , True ],
 [True , False]])

logical_or_ ( y: Tensor, name: str | None = None ) → Tensor [source] logical_or_¶: Inplace version of logical_or API, the output Tensor will be inplaced with input x. Please refer to logical_or.

logical_xor ( y: Tensor, out: Tensor | None = None, name: str | None = None ) → Tensor [source] logical_xor¶

logical_xor operator computes element-wise logical XOR on x and y, and returns out. out is N-dim boolean Tensor. Each element of out is calculated by

\[out = (x || y) \&\& !(x \&\& y)\]

Note

paddle.logical_xor supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be one of bool, int8, int16, int32, int64, bfloat16, float16, float32, float64, complex64, complex128.
y (Tensor) – the input tensor, it’s data type should be one of bool, int8, int16, int32, int64, bfloat16, float16, float32, float64, complex64, complex128.
out (Tensor|None, optional) – The Tensor that specifies the output of the operator, which can be any Tensor that has been created in the program. The default value is None, and a new Tensor will be created to save the output.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. It’s dimension equals with x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([True, False], dtype="bool").reshape([2, 1])
>>> y = paddle.to_tensor([True, False, True, False], dtype="bool").reshape([2, 2])
>>> res = paddle.logical_xor(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=bool, place=Place(cpu), stop_gradient=True,
[[False, True ],
 [True , False]])

logical_xor_ ( y: Tensor, name: str | None = None ) → Tensor [source] logical_xor_¶: Inplace version of logical_xor API, the output Tensor will be inplaced with input x. Please refer to logical_xor.

logit ( eps: float | None = None, name: str | None = None ) → Tensor [source] logit¶

This function generates a new tensor with the logit of the elements of input x. x is clamped to [eps, 1-eps] when eps is not zero. When eps is zero and x < 0 or x > 1, the function will yields NaN.

\[logit(x) = ln(\frac{x}{1 - x})\]

where

\[\begin{split}x_i= \left\{\begin{array}{rcl} x_i & &\text{if } eps == Default \\ eps & &\text{if } x_i < eps \\ x_i & &\text{if } eps <= x_i <= 1-eps \\ 1-eps & &\text{if } x_i > 1-eps \end{array}\right.\end{split}\]

Parameters

x (Tensor) – The input Tensor with data type bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
eps (float|None, optional) – the epsilon for input clamp bound. Default is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

A Tensor with the same data type and shape as x: (integer types are autocasted into float32).

Return type

out(Tensor)

Examples

>>> import paddle

>>> x = paddle.to_tensor([0.2635, 0.0106, 0.2780, 0.2097, 0.8095])
>>> out1 = paddle.logit(x)
>>> out1
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[-1.02785587, -4.53624487, -0.95440406, -1.32673466,  1.44676447])

logit_ ( eps: float | None = None, name: str | None = None ) → Tensor [source] logit_¶: Inplace version of logit API, the output Tensor will be inplaced with input x. Please refer to logit.

logsumexp ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] logsumexp¶

Calculates the log of the sum of exponentials of x along axis .

\[logsumexp(x) = \log\sum exp(x)\]

Parameters

x (Tensor) – The input Tensor with data type bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, which have no more than 4 dimensions.
axis (int|list|tuple|None, optional) – The axis along which to perform logsumexp calculations. axis should be int, list(int) or tuple(int). If axis is a list/tuple of dimension(s), logsumexp is calculated along all element(s) of axis . axis or element(s) of axis should be in range [-D, D), where D is the dimensions of x . If axis or element(s) of axis is less than 0, it works the same way as $axis + D$ . If axis is None, logsumexp is calculated along all elements of x. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keep_dim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of logsumexp along axis of x, with the same data type as x (integer types are autocasted into float32).

Examples:

>>> import paddle

>>> x = paddle.to_tensor([[-1.5, 0., 2.], [3., 1.2, -2.4]])
>>> out1 = paddle.logsumexp(x)
>>> out1
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
3.46912265)
>>> out2 = paddle.logsumexp(x, 1)
>>> out2
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[2.15317822, 3.15684605])

lstsq ( y: Tensor, rcond: float | None = None, driver: Literal['gels', 'gelsy', 'gelsd', 'gelss'] | None = None, name: str | None = None ) → tuple[Tensor, Tensor, Tensor, Tensor] lstsq¶

Computes a solution to the least squares problem of a system of linear equations.

Parameters

x (Tensor) – A tensor with shape (*, M, N) , the data type of the input Tensor x should be one of float32, float64.
y (Tensor) – A tensor with shape (*, M, K) , the data type of the input Tensor y should be one of float32, float64.
rcond (float, optional) – The default value is None. A float pointing number used to determine the effective rank of x. If rcond is None, it will be set to max(M, N) times the machine precision of x_dtype.
driver (str, optional) – The default value is None. The name of LAPACK method to be used. For CPU inputs the valid values are ‘gels’, ‘gelsy’, ‘gelsd, ‘gelss’. For CUDA input, the only valid driver is ‘gels’. If driver is None, ‘gelsy’ is used for CPU inputs and ‘gels’ for CUDA inputs.
name (str, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

A tuple of 4 Tensors which is (solution, residuals, rank, singular_values). solution is a tensor with shape (*, N, K), meaning the least squares solution. residuals is a tensor with shape (*, K), meaning the squared residuals of the solutions, which is computed when M > N and every matrix in x is full-rank, otherwise return an empty tensor. rank is a tensor with shape (*), meaning the ranks of the matrices in x, which is computed when driver in (‘gelsy’, ‘gelsd’, ‘gelss’), otherwise return an empty tensor. singular_values is a tensor with shape (*, min(M, N)), meaning singular values of the matrices in x, which is computed when driver in (‘gelsd’, ‘gelss’), otherwise return an empty tensor.

Return type

Tuple

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 3], [3, 2], [5, 6.]])
>>> y = paddle.to_tensor([[3, 4, 6], [5, 3, 4], [1, 2, 1.]])
>>> results = paddle.linalg.lstsq(x, y, driver="gelsd")
>>> print(results[0])
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 0.78350395, -0.22165027, -0.62371236],
 [-0.11340097,  0.78866047,  1.14948535]])
>>> print(results[1])
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[19.81443405, 10.43814468, 30.56185532])
>>> print(results[2])
Tensor(shape=[], dtype=int32, place=Place(cpu), stop_gradient=True,
2)
>>> print(results[3])
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[9.03455734, 1.54167950])

>>> x = paddle.to_tensor([[10, 2, 3], [3, 10, 5], [5, 6, 12.]])
>>> y = paddle.to_tensor([[4, 2, 9], [2, 0, 3], [2, 5, 3.]])
>>> results = paddle.linalg.lstsq(x, y, driver="gels")
>>> print(results[0])
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 0.39386186,  0.10230169,  0.93606132],
 [ 0.10741688, -0.29028130,  0.11892584],
 [-0.05115093,  0.51918161, -0.19948851]])
>>> print(results[1])
Tensor(shape=[0], dtype=float32, place=Place(cpu), stop_gradient=True,
[])

lu ( pivot=True, get_infos=False, name=None ) → tuple[Tensor, Tensor] | tuple[Tensor, Tensor, Tensor] lu¶

Computes the LU factorization of an N-D(N>=2) matrix x.

Returns the LU factorization(inplace x) and Pivots. low triangular matrix L and upper triangular matrix U are combined to a single LU matrix.

Pivoting is done if pivot is set to True. P mat can be get by pivots:

ones = eye(rows) #eye matrix of rank rows
for i in range(cols):
    swap(ones[i], ones[pivots[i]])
return ones

Parameters

X (Tensor) – the tensor to factor of N-dimensions(N>=2).
pivot (bool, optional) – controls whether pivoting is done. Default: True.
get_infos (bool, optional) – if set to True, returns an info IntTensor. Default: False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

factorization (Tensor), LU matrix, the factorization of input X.

pivots (IntTensor), the pivots of size(*(N-2), min(m,n)). pivots stores all the intermediate transpositions of rows. The final permutation perm could be reconstructed by this, details refer to upper example.

infos (IntTensor, optional), if get_infos is True, this is a tensor of size (*(N-2)) where non-zero values indicate whether factorization for the matrix or each minibatch has succeeded or failed.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]]).astype('float64')
>>> lu,p,info = paddle.linalg.lu(x, get_infos=True)

>>> print(lu)
Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[5.        , 6.        ],
 [0.20000000, 0.80000000],
 [0.60000000, 0.50000000]])
>>> print(p)
Tensor(shape=[2], dtype=int32, place=Place(cpu), stop_gradient=True,
[3, 3])
>>> print(info)
Tensor(shape=[], dtype=int32, place=Place(cpu), stop_gradient=True,
0)

>>> P,L,U = paddle.linalg.lu_unpack(lu,p)

>>> print(P)
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0., 1., 0.],
 [0., 0., 1.],
 [1., 0., 0.]])
>>> print(L)
Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[1.        , 0.        ],
 [0.20000000, 1.        ],
 [0.60000000, 0.50000000]])
>>> print(U)
Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[5.        , 6.        ],
 [0.        , 0.80000000]])

>>> # one can verify : X = P @ L @ U ;

lu_unpack ( y: Tensor, unpack_ludata: bool = True, unpack_pivots: bool = True, name: str | None = None ) → tuple[Tensor, Tensor, Tensor] lu_unpack¶

Unpack L U and P to single matrix tensor . unpack L and U matrix from LU, unpack permutation matrix P from Pivtos .

P mat can be get by pivots:

ones = eye(rows) #eye matrix of rank rows
for i in range(cols):
    swap(ones[i], ones[pivots[i]])

Parameters

x (Tensor) – The LU tensor get from paddle.linalg.lu, which is combined by L and U.
y (Tensor) – Pivots get from paddle.linalg.lu.
unpack_ludata (bool, optional) – whether to unpack L and U from x. Default: True.
unpack_pivots (bool, optional) – whether to unpack permutation matrix P from Pivtos. Default: True.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

P (Tensor), Permutation matrix P of lu factorization.

L (Tensor), The lower triangular matrix tensor of lu factorization.

U (Tensor), The upper triangular matrix tensor of lu factorization.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]]).astype('float64')
>>> lu,p,info = paddle.linalg.lu(x, get_infos=True)

>>> print(lu)
Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[5.        , 6.        ],
 [0.20000000, 0.80000000],
 [0.60000000, 0.50000000]])
>>> print(p)
Tensor(shape=[2], dtype=int32, place=Place(cpu), stop_gradient=True,
[3, 3])
>>> print(info)
Tensor(shape=[1], dtype=int32, place=Place(cpu), stop_gradient=True,
[0])

>>> P,L,U = paddle.linalg.lu_unpack(lu,p)

>>> print(P)
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0., 1., 0.],
 [0., 0., 1.],
 [1., 0., 0.]])
>>> print(L)
Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[1.        , 0.        ],
 [0.20000000, 1.        ],
 [0.60000000, 0.50000000]])
>>> print(U)
Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[5.        , 6.        ],
 [0.        , 0.80000000]])

>>> # one can verify : X = P @ L @ U ;

masked_fill ( mask: Tensor, value: Numeric, name: str | None = None ) → Tensor [source] masked_fill¶

Fills elements of self tensor with value where mask is True. The shape of mask must be broadcastable with the shape of the underlying tensor.

The following figure shows an example: consider a 3x3 matrix x,where all elements have a value of 1, and a matrix mask of the same size, and value is 3.

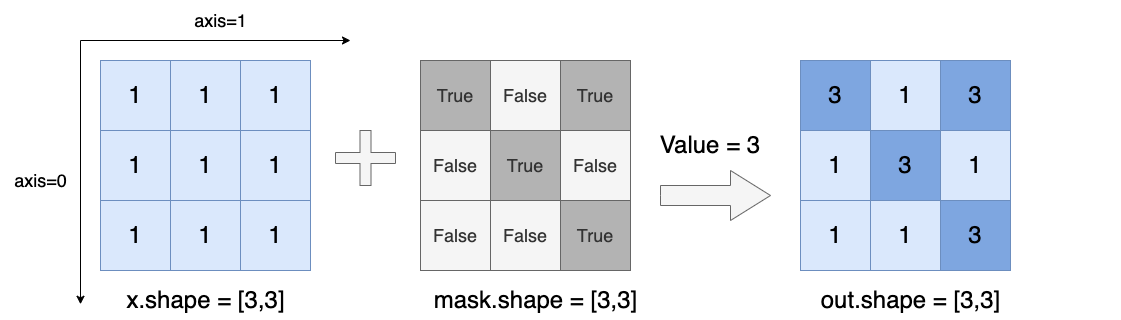
https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/masked_fill.png

Parameters

x (Tensor) – The Destination Tensor. Supported data types are float, double, int, int64_t,float16 and bfloat16.
mask (Tensor) – The boolean tensor indicate the position to be filled. The data type of mask must be bool.
value (Scalar or 0-D Tensor) – The value used to fill the target tensor. Supported data types are float, double, int, int64_t,float16 and bfloat16.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, same dimension and dtype with x.

Examples

>>> 
>>> import paddle
>>> x = paddle.ones((3, 3), dtype="float32")
>>> mask = paddle.to_tensor([[True, True, False]])
>>> print(mask)
Tensor(shape=[1, 3], dtype=bool, place=Place(gpu:0), stop_gradient=True,
       [[True , True , False]])
>>> out = paddle.masked_fill(x, mask, 2)
>>> print(out)
Tensor(shape=[3, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[2., 2., 1.],
        [2., 2., 1.],
        [2., 2., 1.]])

masked_fill_ ( mask: Tensor, value: Numeric, name: str | None = None ) → Tensor [source] masked_fill_¶: Inplace version of masked_fill API, the output Tensor will be inplaced with input x. Please refer to masked_fill.

masked_scatter ( mask: Tensor, value: Tensor, name: str | None = None ) → Tensor [source] masked_scatter¶

Copies elements from value into x tensor at positions where the mask is True.

Elements from source are copied into x starting at position 0 of value and continuing in order one-by-one for each occurrence of mask being True. The shape of mask must be broadcastable with the shape of the underlying tensor. The value should have at least as many elements as the number of ones in mask.

The image illustrates a typical case of the masked_scatter operation.

Tensor value: Contains the data to be filled into the target tensor. Only the parts where the mask is True will take values from the value tensor, while the rest will be ignored;

Tensor mask: Specifies which positions should extract values from the value tensor and update the target tensor. True indicates the corresponding position needs to be updated;

Tensor origin: The input tensor, where only the parts satisfying the mask will be replaced, and the rest remains unchanged;

Result: After the masked_scatter operation, the parts of the origin tensor where the mask is True are updated with the corresponding values from the value tensor, while the parts where the mask is False remain unchanged, forming the final updated tensor.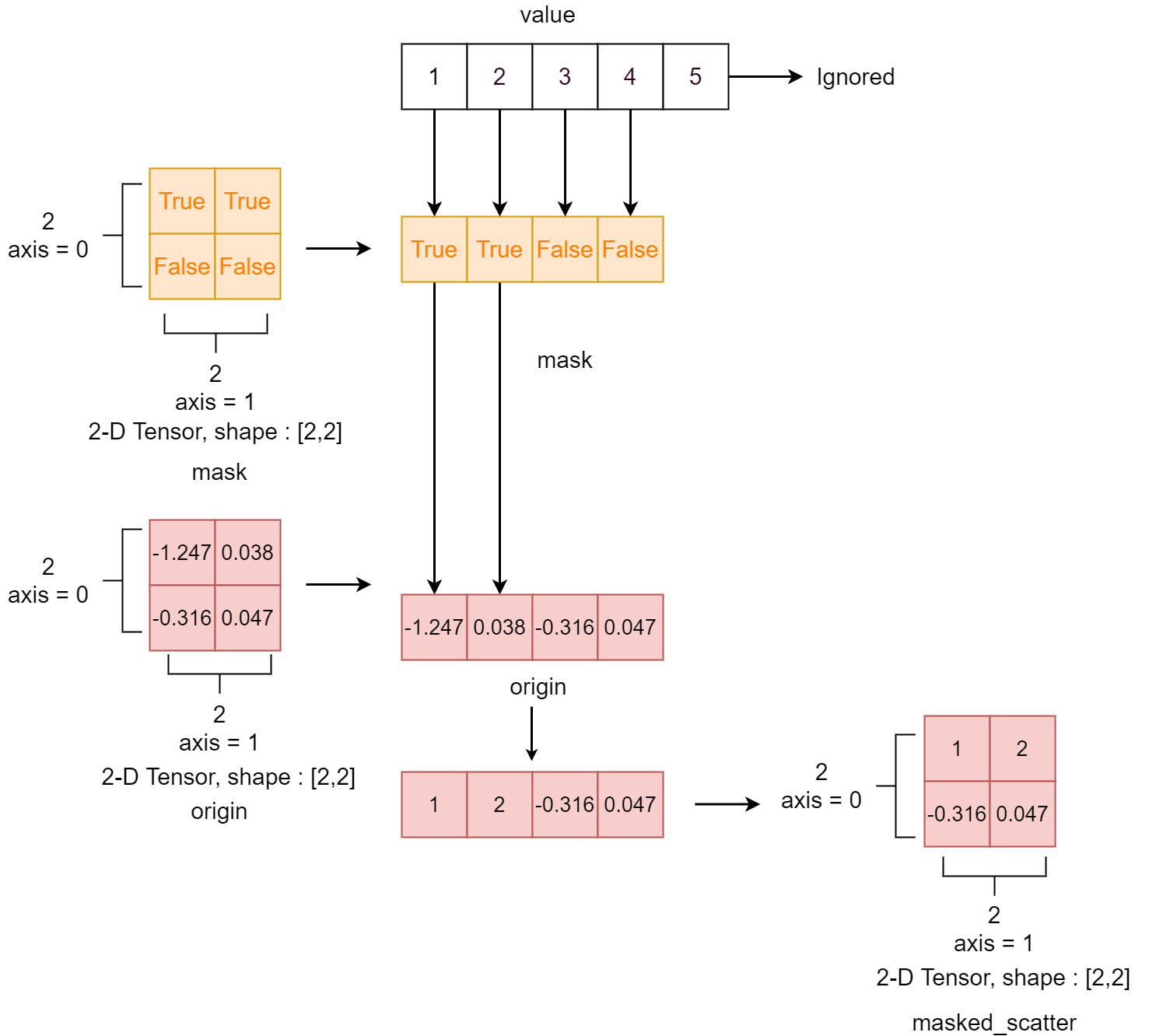

Parameters

x (Tensor) – An N-D Tensor. The data type is float16, float32, float64, int32, int64 or bfloat16.
mask (Tensor) – The boolean tensor indicate the position to be filled. The data type of mask must be bool.
value (Tensor) – The value used to fill the target tensor. Supported data types are same as x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A reshaped Tensor with the same data type as x.

Examples

>>> import paddle
>>> paddle.seed(2048)
>>> x = paddle.randn([2, 2])
>>> print(x)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
    [[-1.24725831,  0.03843464],
    [-0.31660911,  0.04793844]])

>>> mask = paddle.to_tensor([[True, True], [False, False]])
>>> value = paddle.to_tensor([1, 2, 3, 4, 5,], dtype="float32")

>>> out = paddle.masked_scatter(x, mask, value)
>>> print(out)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
    [[1,  2],
    [-0.31660911,  0.04793844]])

masked_scatter_ ( mask: Tensor, value: Tensor, name: str | None = None ) → Tensor [source] masked_scatter_¶: Inplace version of masked_scatter API, the output Tensor will be inplaced with input x. Please refer to masked_scatter.

masked_select ( mask: Tensor, name: str | None = None ) → Tensor [source] masked_select¶

Returns a new 1-D tensor which indexes the input tensor according to the mask which is a tensor with data type of bool.

Note

paddle.masked_select supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – The input Tensor, the data type can be int32, int64, uint16, float16, float32, float64.
mask (Tensor) – The Tensor containing the binary mask to index with, it’s data type is bool.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, A 1-D Tensor which is the same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0, 3.0, 4.0],
...                       [5.0, 6.0, 7.0, 8.0],
...                       [9.0, 10.0, 11.0, 12.0]])
>>> mask = paddle.to_tensor([[True, False, False, False],
...                          [True, True, False, False],
...                          [True, False, False, False]])
>>> out = paddle.masked_select(x, mask)
>>> print(out.numpy())
[1. 5. 6. 9.]

matmul ( y: Tensor, transpose_x: bool = False, transpose_y: bool = False, name: str | None = None ) → Tensor [source] matmul¶

Applies matrix multiplication to two tensors. matmul follows the complete broadcast rules, and its behavior is consistent with np.matmul.

Currently, the input tensors’ number of dimensions can be any, matmul can be used to achieve the dot, matmul and batchmatmul.

The actual behavior depends on the shapes of $x$, $y$ and the flag values of transpose_x, transpose_y. Specifically:

If a transpose flag is specified, the last two dimensions of the tensor are transposed. If the tensor is ndim-1 of shape, the transpose is invalid. If the tensor is ndim-1 of shape $[D]$, then for $x$ it is treated as $[1, D]$, whereas for $y$ it is the opposite: It is treated as $[D, 1]$.

The multiplication behavior depends on the dimensions of x and y. Specifically:

If both tensors are 1-dimensional, the dot product result is obtained.
If both tensors are 2-dimensional, the matrix-matrix product is obtained.
If the x is 1-dimensional and the y is 2-dimensional, a 1 is prepended to its dimension in order to conduct the matrix multiply. After the matrix multiply, the prepended dimension is removed.
If the x is 2-dimensional and y is 1-dimensional, the matrix-vector product is obtained.
If both arguments are at least 1-dimensional and at least one argument is N-dimensional (where N > 2), then a batched matrix multiply is obtained. If the first argument is 1-dimensional, a 1 is prepended to its dimension in order to conduct the batched matrix multiply and removed after. If the second argument is 1-dimensional, a 1 is appended to its dimension for the purpose of the batched matrix multiple and removed after. The non-matrix (exclude the last two dimensions) dimensions are broadcasted according the broadcast rule. For example, if input is a (j, 1, n, m) tensor and the other is a (k, m, p) tensor, out will be a (j, k, n, p) tensor.

Parameters

x (Tensor) – The input tensor which is a Tensor.
y (Tensor) – The input tensor which is a Tensor.
transpose_x (bool, optional) – Whether to transpose $x$ before multiplication. Default is False.
transpose_y (bool, optional) – Whether to transpose $y$ before multiplication. Default is False.
name (str|None, optional) – If set None, the layer will be named automatically. For more information, please refer to Name. Default is None.

Returns

The output Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> # vector * vector
>>> x = paddle.rand([10])
>>> y = paddle.rand([10])
>>> z = paddle.matmul(x, y)
>>> print(z.shape)
[]

>>> # matrix * vector
>>> x = paddle.rand([10, 5])
>>> y = paddle.rand([5])
>>> z = paddle.matmul(x, y)
>>> print(z.shape)
[10]

>>> # batched matrix * broadcasted vector
>>> x = paddle.rand([10, 5, 2])
>>> y = paddle.rand([2])
>>> z = paddle.matmul(x, y)
>>> print(z.shape)
[10, 5]

>>> # batched matrix * batched matrix
>>> x = paddle.rand([10, 5, 2])
>>> y = paddle.rand([10, 2, 5])
>>> z = paddle.matmul(x, y)
>>> print(z.shape)
[10, 5, 5]

>>> # batched matrix * broadcasted matrix
>>> x = paddle.rand([10, 1, 5, 2])
>>> y = paddle.rand([1, 3, 2, 5])
>>> z = paddle.matmul(x, y)
>>> print(z.shape)
[10, 3, 5, 5]

matrix_power ( n: int, name: str | None = None ) → tuple[Tensor, int] matrix_power¶

Computes the n-th power of a square matrix or a batch of square matrices.

Let $X$ be a square matrix or a batch of square matrices, $n$ be an exponent, the equation should be:

\[Out = X ^ {n}\]

Specifically,

If n > 0, it returns the matrix or a batch of matrices raised to the power of n.
If n = 0, it returns the identity matrix or a batch of identity matrices.
If n < 0, it returns the inverse of each matrix (if invertible) raised to the power of abs(n).

Parameters

x (Tensor) – A square matrix or a batch of square matrices to be raised to power n. Its shape should be [*, M, M], where * is zero or more batch dimensions. Its data type should be float32 or float64.
n (int) – The exponent. It can be any positive, negative integer or zero.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, The n-th power of the matrix (or the batch of matrices) x. Its data type should be the same as that of x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2, 3],
...                       [1, 4, 9],
...                       [1, 8, 27]], dtype='float64')
>>> print(paddle.linalg.matrix_power(x, 2))
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[6.  , 34. , 102.],
 [14. , 90. , 282.],
 [36. , 250., 804.]])

>>> print(paddle.linalg.matrix_power(x, 0))
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[1., 0., 0.],
 [0., 1., 0.],
 [0., 0., 1.]])

>>> print(paddle.linalg.matrix_power(x, -2))
Tensor(shape=[3, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[ 12.91666667, -12.75000000,  2.83333333 ],
 [-7.66666667 ,  8.         , -1.83333333 ],
 [ 1.80555556 , -1.91666667 ,  0.44444444 ]])

matrix_transpose ( name: Optional[str] = None ) → Tensor [source] matrix_transpose¶

Transpose the last two dimensions of the input tensor x.

Note

If n is the number of dimensions of x, paddle.matrix_transpose(x) is equivalent to x.transpose([0, 1, …, n-2, n-1]).

Parameters

x (Tensor) – The input tensor to be transposed. x must be an N-dimensional tensor (N >= 2) of any data type supported by Paddle.
name (str|None, optional) – The name of this layer. For more information, please refer to Name. Default is None.

Returns

A new tensor with the same shape as x, except that the last two dimensions are transposed.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.ones(shape=[2, 3, 5])
>>> x_transposed = paddle.matrix_transpose(x)
>>> print(x_transposed.shape)
[2, 5, 3]

max ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] max¶

Computes the maximum of tensor elements over the given axis.

Note

The difference between max and amax is: If there are multiple maximum elements, amax evenly distributes gradient between these equal values, while max propagates gradient to all of them.

Parameters

x (Tensor) – A tensor, the data type is float8_e4m3fn, float8_e5m2, bfloat16, float16, float32, float64, int32, int64.
axis (int|list|tuple|None, optional) – The axis along which the maximum is computed. If None, compute the maximum over all elements of x and return a Tensor with a single element, otherwise must be in the range $[-x.ndim(x), x.ndim(x))$. If $axis[i] < 0$, the axis to reduce is $x.ndim + axis[i]$.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of maximum on the specified axis of input tensor, it’s data type is the same as x.

Examples

>>> import paddle

>>> # data_x is a Tensor with shape [2, 4]
>>> # the axis is a int element
>>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9],
...                       [0.1, 0.2, 0.6, 0.7]],
...                       dtype='float64', stop_gradient=False)
>>> result1 = paddle.max(x)
>>> result1.backward()
>>> result1
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False,
0.90000000)
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0., 0., 0., 1.],
 [0., 0., 0., 0.]])

>>> x.clear_grad()
>>> result2 = paddle.max(x, axis=0)
>>> result2.backward()
>>> result2
Tensor(shape=[4], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.20000000, 0.30000000, 0.60000000, 0.90000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[1., 1., 0., 1.],
 [0., 0., 1., 0.]])

>>> x.clear_grad()
>>> result3 = paddle.max(x, axis=-1)
>>> result3.backward()
>>> result3
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.90000000, 0.70000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0., 0., 0., 1.],
 [0., 0., 0., 1.]])

>>> x.clear_grad()
>>> result4 = paddle.max(x, axis=1, keepdim=True)
>>> result4.backward()
>>> result4
Tensor(shape=[2, 1], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.90000000],
 [0.70000000]])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0., 0., 0., 1.],
 [0., 0., 0., 1.]])

>>> # data_y is a Tensor with shape [2, 2, 2]
>>> # the axis is list
>>> y = paddle.to_tensor([[[1.0, 2.0], [3.0, 4.0]],
...                         [[5.0, 6.0], [7.0, 8.0]]],
...                         dtype='float64', stop_gradient=False)
>>> result5 = paddle.max(y, axis=[1, 2])
>>> result5.backward()
>>> result5
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[4., 8.])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[0., 0.],
  [0., 1.]],
 [[0., 0.],
  [0., 1.]]])

>>> y.clear_grad()
>>> result6 = paddle.max(y, axis=[0, 1])
>>> result6.backward()
>>> result6
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[7., 8.])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[0., 0.],
  [0., 0.]],
 [[0., 0.],
  [1., 1.]]])

maximum ( y: Tensor, name: str | None = None ) → Tensor [source] maximum¶

Compare two tensors and returns a new tensor containing the element-wise maxima. The equation is:

\[out = max(x, y)\]

Note

paddle.maximum supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2], [7, 8]])
>>> y = paddle.to_tensor([[3, 4], [5, 6]])
>>> res = paddle.maximum(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 4],
 [7, 8]])

>>> x = paddle.to_tensor([[1, 2, 3], [1, 2, 3]])
>>> y = paddle.to_tensor([3, 0, 4])
>>> res = paddle.maximum(x, y)
>>> print(res)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 2, 4],
 [3, 2, 4]])

>>> x = paddle.to_tensor([2, 3, 5], dtype='float32')
>>> y = paddle.to_tensor([1, float("nan"), float("nan")], dtype='float32')
>>> res = paddle.maximum(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[2. , nan, nan])

>>> x = paddle.to_tensor([5, 3, float("inf")], dtype='float32')
>>> y = paddle.to_tensor([1, -float("inf"), 5], dtype='float32')
>>> res = paddle.maximum(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[5.  , 3.  , inf.])

mean ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] mean¶

Computes the mean of the input tensor’s elements along axis.

Parameters

x (Tensor) – The input Tensor with data type bool, bfloat16, float16, float32, float64, int32, int64, complex64, complex128.
axis (int|list|tuple|None, optional) – The axis along which to perform mean calculations. axis should be int, list(int) or tuple(int). If axis is a list/tuple of dimension(s), mean is calculated along all element(s) of axis . axis or element(s) of axis should be in range [-D, D), where D is the dimensions of x . If axis or element(s) of axis is less than 0, it works the same way as $axis + D$ . If axis is None, mean is calculated over all elements of x. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keepdim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of average along axis of x, with the same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[[1., 2., 3., 4.],
...                        [5., 6., 7., 8.],
...                        [9., 10., 11., 12.]],
...                       [[13., 14., 15., 16.],
...                        [17., 18., 19., 20.],
...                        [21., 22., 23., 24.]]])
>>> out1 = paddle.mean(x)
>>> print(out1.numpy())
12.5
>>> out2 = paddle.mean(x, axis=-1)
>>> print(out2.numpy())
[[ 2.5  6.5 10.5]
 [14.5 18.5 22.5]]
>>> out3 = paddle.mean(x, axis=-1, keepdim=True)
>>> print(out3.numpy())
[[[ 2.5]
  [ 6.5]
  [10.5]]
 [[14.5]
  [18.5]
  [22.5]]]
>>> out4 = paddle.mean(x, axis=[0, 2])
>>> print(out4.numpy())
[ 8.5 12.5 16.5]

median ( axis=None, keepdim=False, mode='avg', name=None ) [source] median¶

Compute the median along the specified axis.

Parameters

x (Tensor) – The input Tensor, it’s data type can be bfloat16, float16, float32, float64, int32, int64.
axis (int|None, optional) – The axis along which to perform median calculations axis should be int. axis should be in range [-D, D), where D is the dimensions of x . If axis is less than 0, it works the same way as $axis + D$. If axis is None, median is calculated over all elements of x. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keepdim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
mode (str, optional) – Whether to use mean or min operation to calculate the median values when the input tensor has an even number of elements in the dimension axis. Support ‘avg’ and ‘min’. Default is ‘avg’.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor or tuple of Tensor. If mode == ‘avg’, the result will be the tensor of median values; If mode == ‘min’ and axis is None, the result will be the tensor of median values; If mode == ‘min’ and axis is not None, the result will be a tuple of two tensors containing median values and their indices.

When mode == ‘avg’, if data type of x is float64, data type of median values will be float64, otherwise data type of median values will be float32. When mode == ‘min’, the data type of median values will be the same as x. The data type of indices will be int64.

Examples

>>> import paddle
>>> import numpy as np

>>> x = paddle.arange(12).reshape([3, 4])
>>> print(x)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0 , 1 , 2 , 3 ],
 [4 , 5 , 6 , 7 ],
 [8 , 9 , 10, 11]])

>>> y1 = paddle.median(x)
>>> print(y1)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
5.50000000)

>>> y2 = paddle.median(x, axis=0)
>>> print(y2)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[4., 5., 6., 7.])

>>> y3 = paddle.median(x, axis=1)
>>> print(y3)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.50000000, 5.50000000, 9.50000000])

>>> y4 = paddle.median(x, axis=0, keepdim=True)
>>> print(y4)
Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[4., 5., 6., 7.]])

>>> y5 = paddle.median(x, mode='min')
>>> print(y5)
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
5)

>>> median_value, median_indices = paddle.median(x, axis=1, mode='min')
>>> print(median_value)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 5, 9])
>>> print(median_indices)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 1, 1])

>>> # cases containing nan values
>>> x = paddle.to_tensor(np.array([[1,float('nan'),3,float('nan')],[1,2,3,4],[float('nan'),1,2,3]]))

>>> y6 = paddle.median(x, axis=-1, keepdim=True)
>>> print(y6)
Tensor(shape=[3, 1], dtype=float64, place=Place(cpu), stop_gradient=True,
[[nan       ],
 [2.50000000],
 [nan       ]])

>>> median_value, median_indices = paddle.median(x, axis=1, keepdim=True, mode='min')
>>> print(median_value)
Tensor(shape=[3, 1], dtype=float64, place=Place(cpu), stop_gradient=True,
[[nan],
 [2. ],
 [nan]])
>>> print(median_indices)
Tensor(shape=[3, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1],
 [1],
 [0]])

min ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] min¶

Computes the minimum of tensor elements over the given axis

Note

The difference between min and amin is: If there are multiple minimum elements, amin evenly distributes gradient between these equal values, while min propagates gradient to all of them.

Parameters

x (Tensor) – A tensor, the data type is bfloat16, float16, float32, float64, int32, int64.
axis (int|list|tuple|None, optional) – The axis along which the minimum is computed. If None, compute the minimum over all elements of x and return a Tensor with a single element, otherwise must be in the range $[-x.ndim, x.ndim)$. If $axis[i] < 0$, the axis to reduce is $x.ndim + axis[i]$.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of minimum on the specified axis of input tensor, it’s data type is the same as input’s Tensor.

Examples

>>> import paddle

>>> # data_x is a Tensor with shape [2, 4]
>>> # the axis is a int element
>>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9],
...                       [0.1, 0.2, 0.6, 0.7]],
...                       dtype='float64', stop_gradient=False)
>>> result1 = paddle.min(x)
>>> result1.backward()
>>> result1
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=False,
0.10000000)
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0., 0., 0., 0.],
 [1., 0., 0., 0.]])

>>> x.clear_grad()
>>> result2 = paddle.min(x, axis=0)
>>> result2.backward()
>>> result2
Tensor(shape=[4], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.10000000, 0.20000000, 0.50000000, 0.70000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0., 0., 1., 0.],
 [1., 1., 0., 1.]])

>>> x.clear_grad()
>>> result3 = paddle.min(x, axis=-1)
>>> result3.backward()
>>> result3
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[0.20000000, 0.10000000])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[1., 0., 0., 0.],
 [1., 0., 0., 0.]])

>>> x.clear_grad()
>>> result4 = paddle.min(x, axis=1, keepdim=True)
>>> result4.backward()
>>> result4
Tensor(shape=[2, 1], dtype=float64, place=Place(cpu), stop_gradient=False,
[[0.20000000],
 [0.10000000]])
>>> x.grad
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=False,
[[1., 0., 0., 0.],
 [1., 0., 0., 0.]])

>>> # data_y is a Tensor with shape [2, 2, 2]
>>> # the axis is list
>>> y = paddle.to_tensor([[[1.0, 2.0], [3.0, 4.0]],
...                       [[5.0, 6.0], [7.0, 8.0]]],
...                       dtype='float64', stop_gradient=False)
>>> result5 = paddle.min(y, axis=[1, 2])
>>> result5.backward()
>>> result5
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[1., 5.])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[1., 0.],
  [0., 0.]],
 [[1., 0.],
  [0., 0.]]])

>>> y.clear_grad()
>>> result6 = paddle.min(y, axis=[0, 1])
>>> result6.backward()
>>> result6
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=False,
[1., 2.])
>>> y.grad
Tensor(shape=[2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=False,
[[[1., 1.],
  [0., 0.]],
 [[0., 0.],
  [0., 0.]]])

minimum ( y: Tensor, name: str | None = None ) → Tensor [source] minimum¶

Compare two tensors and return a new tensor containing the element-wise minima. The equation is:

\[out = min(x, y)\]

Note

paddle.minimum supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2], [7, 8]])
>>> y = paddle.to_tensor([[3, 4], [5, 6]])
>>> res = paddle.minimum(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 2],
 [5, 6]])

>>> x = paddle.to_tensor([[[1, 2, 3], [1, 2, 3]]])
>>> y = paddle.to_tensor([3, 0, 4])
>>> res = paddle.minimum(x, y)
>>> print(res)
Tensor(shape=[1, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[1, 0, 3],
  [1, 0, 3]]])

>>> x = paddle.to_tensor([2, 3, 5], dtype='float32')
>>> y = paddle.to_tensor([1, float("nan"), float("nan")], dtype='float32')
>>> res = paddle.minimum(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1. , nan, nan])

>>> x = paddle.to_tensor([5, 3, float("inf")], dtype='float64')
>>> y = paddle.to_tensor([1, -float("inf"), 5], dtype='float64')
>>> res = paddle.minimum(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True,
[ 1.  , -inf.,  5.  ])

mm ( mat2: Tensor, name: str | None = None ) → Tensor [source] mm¶

Applies matrix multiplication to two tensors.

Currently, the input tensors’ rank can be any, but when the rank of any inputs is bigger than 3, this two inputs’ rank should be equal.

Also note that if the raw tensor $x$ or $mat2$ is rank-1 and nontransposed, the prepended or appended dimension $1$ will be removed after matrix multiplication.

Parameters

input (Tensor) – The input tensor which is a Tensor. Support data types: bfloat16, float16, float32, float64, int8, int32, int64, complex64, complex128.
mat2 (Tensor) – The input tensor which is a Tensor. Support data types: bfloat16, float16, float32, float64, int8, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The product Tensor, with same data type of the input Tensor.

Return type

Tensor

* example 1:

input: [B, ..., M, K], mat2: [B, ..., K, N]
out: [B, ..., M, N]

* example 2:

input: [B, M, K], mat2: [B, K, N]
out: [B, M, N]

* example 3:

input: [B, M, K], mat2: [K, N]
out: [B, M, N]

* example 4:

input: [M, K], mat2: [K, N]
out: [M, N]

* example 5:

input: [B, M, K], mat2: [K]
out: [B, M]

* example 6:

input: [K], mat2: [K]
out: [1]

Examples

>>> import paddle
>>> input = paddle.arange(1, 7).reshape((3, 2)).astype('float32')
>>> mat2 = paddle.arange(1, 9).reshape((2, 4)).astype('float32')
>>> out = paddle.mm(input, mat2)
>>> out
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[11., 14., 17., 20.],
 [23., 30., 37., 44.],
 [35., 46., 57., 68.]])

mod ( y: Tensor, name: str | None = None ) → Tensor [source] mod¶

Mod two tensors element-wise. The equation is:

\[out = x \% y\]

Note

paddle.remainder supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

And mod, floor_mod are all functions with the same name

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 8, 7])
>>> y = paddle.to_tensor([1, 5, 3, 3])
>>> z = paddle.remainder(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

>>> z = paddle.floor_mod(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

>>> z = paddle.mod(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

mod_ ( y: Tensor, name: str | None = None ) → Tensor [source] mod_¶: Inplace version of floor_mod_ API, the output Tensor will be inplaced with input x. Please refer to floor_mod_.

mode ( axis: int = -1, keepdim: bool = False, name: str | None = None ) → tuple[Tensor, Tensor] [source] mode¶

Used to find values and indices of the modes at the optional axis.

Parameters

x (Tensor) – Tensor, an input N-D Tensor with type float32, float64, int32, int64.
axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is -1.
keepdim (bool, optional) – Whether to keep the given axis in output. If it is True, the dimensions will be same as input x and with size one in the axis. Otherwise the output dimensions is one fewer than x since the axis is squeezed. Default is False.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

tuple (Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.

Examples

>>> import paddle

>>> tensor = paddle.to_tensor([[[1,2,2],[2,3,3]],[[0,5,5],[9,9,0]]], dtype=paddle.float32)
>>> res = paddle.mode(tensor, 2)
>>> print(res)
(Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[2., 3.],
 [5., 9.]]), Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[2, 2],
 [2, 1]]))

moveaxis ( source: int | Sequence[int], destination: int | Sequence[int], name: str | None = None ) → Tensor [source] moveaxis¶

Move the axis of tensor from source position to destination position.

Other axis that have not been moved remain their original order.

Parameters

x (Tensor) – The input Tensor. It is a N-D Tensor of data types bool, int32, int64, float32, float64, complex64, complex128.
source (int|tuple|list) – source position of axis that will be moved. Each element must be unique and integer.
destination (int|tuple|list) – destination position of axis that has been moved. Each element must be unique and integer.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, A new tensor whose axis have been moved.

Examples

>>> import paddle

>>> x = paddle.ones([3, 2, 4])
>>> outshape = paddle.moveaxis(x, [0, 1], [1, 2]).shape
>>> print(outshape)
[4, 3, 2]

>>> x = paddle.ones([2, 3])
>>> outshape = paddle.moveaxis(x, 0, 1).shape # equivalent to paddle.t(x)
>>> print(outshape)
[3, 2]

multi_dot ( name: str | None = None ) → Tensor multi_dot¶

Multi_dot is an operator that calculates multiple matrix multiplications.

Supports inputs of float16(only GPU support), float32 and float64 dtypes. This function does not support batched inputs.

The input tensor in [x] must be 2-D except for the first and last can be 1-D. If the first tensor is a 1-D vector of shape(n, ) it is treated as row vector of shape(1, n), similarly if the last tensor is a 1D vector of shape(n, ), it is treated as a column vector of shape(n, 1).

If the first and last tensor are 2-D matrix, then the output is also 2-D matrix, otherwise the output is a 1-D vector.

Multi_dot will select the lowest cost multiplication order for calculation. The cost of multiplying two matrices with shapes (a, b) and (b, c) is a * b * c. Given matrices A, B, C with shapes (20, 5), (5, 100), (100, 10) respectively, we can calculate the cost of different multiplication orders as follows: - Cost((AB)C) = 20x5x100 + 20x100x10 = 30000 - Cost(A(BC)) = 5x100x10 + 20x5x10 = 6000

In this case, multiplying B and C first, then multiply A, which is 5 times faster than sequential calculation.

Parameters

x (list[Tensor]) – The input tensors which is a list Tensor.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> # A * B
>>> A = paddle.rand([3, 4])
>>> B = paddle.rand([4, 5])
>>> out = paddle.linalg.multi_dot([A, B])
>>> print(out.shape)
[3, 5]

>>> # A * B * C
>>> A = paddle.rand([10, 5])
>>> B = paddle.rand([5, 8])
>>> C = paddle.rand([8, 7])
>>> out = paddle.linalg.multi_dot([A, B, C])
>>> print(out.shape)
[10, 7]

multigammaln ( p: int, name: str | None = None ) → Tensor [source] multigammaln¶

This function computes the log of multivariate gamma, also sometimes called the generalized gamma.

Parameters

x (Tensor) – Input Tensor. Must be one of the following types: float16, float32, float64, uint16.
p (int) – The dimension of the space of integration.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The values of the log multivariate gamma at the given tensor x.

Return type

out (Tensor)

Examples

>>> import paddle

>>> x = paddle.to_tensor([2.5, 3.5, 4, 6.5, 7.8, 10.23, 34.25])
>>> p = 2
>>> out = paddle.multigammaln(x, p)
>>> print(out)
Tensor(shape=[7], dtype=float32, place=Place(cpu), stop_gradient=True,
    [0.85704780  , 2.46648574  , 3.56509781  , 11.02241898 , 15.84497833 ,
        26.09257698 , 170.68318176])

multigammaln_ ( p: int, name: str | None = None ) → Tensor [source] multigammaln_¶: Inplace version of multigammaln_ API, the output Tensor will be inplaced with input x. Please refer to multigammaln.

multinomial ( num_samples: int = 1, replacement: bool = False, name: str | None = None ) → Tensor [source] multinomial¶

Returns a Tensor filled with random values sampled from a Multinomical distribution. The input x is a tensor with probabilities for generating the random number. Each element in x should be larger or equal to 0, but not all 0. replacement indicates whether it is a replaceable sample. If replacement is True, a category can be sampled more than once.

Parameters

x (Tensor) – A tensor with probabilities for generating the random number. The data type should be float32, float64.
num_samples (int, optional) – Number of samples, default is 1.
replacement (bool, optional) – Whether it is a replaceable sample, default is False.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, A Tensor filled with sampled category index after num_samples times samples.

Examples

>>> import paddle
>>> paddle.seed(100) # on CPU device

>>> x = paddle.rand([2,4])
>>> print(x)
>>> 
Tensor(shape=[2, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.55355281, 0.20714243, 0.01162981, 0.51577556],
 [0.36369765, 0.26091650, 0.18905126, 0.56219709]])
>>> 

>>> paddle.seed(200) # on CPU device
>>> out1 = paddle.multinomial(x, num_samples=5, replacement=True)
>>> print(out1)
>>> 
Tensor(shape=[2, 5], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 3, 0, 0, 0],
 [3, 3, 3, 1, 0]])
>>> 

>>> # out2 = paddle.multinomial(x, num_samples=5)
>>> # InvalidArgumentError: When replacement is False, number of samples
>>> #  should be less than non-zero categories

>>> paddle.seed(300) # on CPU device
>>> out3 = paddle.multinomial(x, num_samples=3)
>>> print(out3)
>>> 
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3, 0, 1],
 [3, 1, 0]])
>>> 

multiplex ( index: Tensor, name: str | None = None ) → Tensor [source] multiplex¶

Based on the given index parameter, the OP selects a specific row from each input Tensor to construct the output Tensor.

If the input of this OP contains $m$ Tensors, where $I_{i}$ means the i-th input Tensor, $i$ between $[0,m)$ .

And $O$ means the output, where $O[i]$ means the i-th row of the output, then the output satisfies that $O[i] = I_{index[i]}[i]$ .

For Example:

Given:

inputs = [[[0,0,3,4], [0,1,3,4], [0,2,4,4], [0,3,3,4]],
          [[1,0,3,4], [1,1,7,8], [1,2,4,2], [1,3,3,4]],
          [[2,0,3,4], [2,1,7,8], [2,2,4,2], [2,3,3,4]],
          [[3,0,3,4], [3,1,7,8], [3,2,4,2], [3,3,3,4]]]

index = [[3],[0],[1],[2]]

out = [[3,0,3,4],    # out[0] = inputs[index[0]][0] = inputs[3][0] = [3,0,3,4]
       [0,1,3,4],    # out[1] = inputs[index[1]][1] = inputs[0][1] = [0,1,3,4]
       [1,2,4,2],    # out[2] = inputs[index[2]][2] = inputs[1][2] = [1,2,4,2]
       [2,3,3,4]]    # out[3] = inputs[index[3]][3] = inputs[2][3] = [2,3,3,4]

Parameters

inputs (list[Tensor]|tuple[Tensor, ...]) – The input Tensor list. The list elements are N-D Tensors of data types float32, float64, int32, int64, complex64, complex128. All input Tensor shapes should be the same and rank must be at least 2.
index (Tensor) – Used to select some rows in the input Tensor to construct an index of the output Tensor. It is a 2-D Tensor with data type int32 or int64 and shape [M, 1], where M is the number of input Tensors.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Output of multiplex OP, with data type being float32, float64, int32, int64.

Return type

Tensor

Examples

>>> import paddle

>>> img1 = paddle.to_tensor([[1, 2], [3, 4]], dtype=paddle.float32)
>>> img2 = paddle.to_tensor([[5, 6], [7, 8]], dtype=paddle.float32)
>>> inputs = [img1, img2]
>>> index = paddle.to_tensor([[1], [0]], dtype=paddle.int32)
>>> res = paddle.multiplex(inputs, index)
>>> print(res)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[5., 6.],
 [3., 4.]])

multiply ( y: Tensor, name: str | None = None ) → Tensor [source] multiply¶

multiply two tensors element-wise. The equation is:

\[out = x * y\]

Note

Supported shape of x and y for this operator: 1. x.shape == y.shape. 2. x.shape could be the continuous subsequence of y.shape. paddle.multiply supports broadcasting. If you would like to know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, its data type should be one of bfloat16, float16, float32, float64, int32, int64, bool, complex64, complex128.
y (Tensor) – the input tensor, its data type should be one of bfloat16, float16, float32, float64, int32, int64, bool, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2], [3, 4]])
>>> y = paddle.to_tensor([[5, 6], [7, 8]])
>>> res = paddle.multiply(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[5 , 12],
 [21, 32]])
>>> x = paddle.to_tensor([[[1, 2, 3], [1, 2, 3]]])
>>> y = paddle.to_tensor([2])
>>> res = paddle.multiply(x, y)
>>> print(res)
Tensor(shape=[1, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[2, 4, 6],
  [2, 4, 6]]])

multiply_ ( y: Tensor, name: str | None = None ) → Tensor [source] multiply_¶: Inplace version of multiply API, the output Tensor will be inplaced with input x. Please refer to multiply.

mv ( vec: Tensor, name: str | None = None ) → Tensor [source] mv¶

Performs a matrix-vector product of the matrix x and the vector vec.

Parameters

x (Tensor) – A tensor with shape $[M, N]$ , The data type of the input Tensor x should be one of float32, float64.
vec (Tensor) – A tensor with shape $[N]$ , The data type of the input Tensor x should be one of float32, float64.
name (str|None, optional) – Normally there is no need for user to set this property. For more information, please refer to Name. Default is None.

Returns

The tensor which is produced by x and vec.

Return type

Tensor

Examples

>>> # x: [M, N], vec: [N]
>>> # paddle.mv(x, vec)  # out: [M]

>>> import paddle

>>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1]]).astype("float64")
>>> vec = paddle.to_tensor([3, 5, 1]).astype("float64")
>>> out = paddle.mv(x, vec)
>>> print(out)
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=True,
[14., 10.])

name

Tensor’s name.

Returns: Tensor’s name.
Return type: str

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.)
>>> print(x.name)
generated_tensor_0
>>> x.name = 'test_tensor_name'
>>> print(x.name)
test_tensor_name

nan_to_num ( nan: float = 0.0, posinf: float | None = None, neginf: float | None = None, name: str | None = None ) → Tensor [source] nan_to_num¶

Replaces NaN, positive infinity, and negative infinity values in input tensor.

Parameters

x (Tensor) – An N-D Tensor, the data type is float32, float64.
nan (float, optional) – the value to replace NaNs with. Default is 0.
posinf (float|None, optional) – if a Number, the value to replace positive infinity values with. If None, positive infinity values are replaced with the greatest finite value representable by input’s dtype. Default is None.
neginf (float|None, optional) – if a Number, the value to replace negative infinity values with. If None, negative infinity values are replaced with the lowest finite value representable by input’s dtype. Default is None.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Results of nan_to_num operation input Tensor x.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([float('nan'), 0.3, float('+inf'), float('-inf')], dtype='float32')
>>> out1 = paddle.nan_to_num(x)
>>> out1
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 0.                                      ,
  0.30000001                              ,
  340282346638528859811704183484516925440.,
 -340282346638528859811704183484516925440.])
>>> out2 = paddle.nan_to_num(x, nan=1)
>>> out2
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 1.                                      ,
  0.30000001                              ,
  340282346638528859811704183484516925440.,
 -340282346638528859811704183484516925440.])
>>> out3 = paddle.nan_to_num(x, posinf=5)
>>> out3
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 0.                                      ,
  0.30000001                              ,
  5.                                      ,
 -340282346638528859811704183484516925440.])
>>> out4 = paddle.nan_to_num(x, nan=10, neginf=-99)
>>> out4
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 10.                                    ,
  0.30000001                             ,
 340282346638528859811704183484516925440.,
 -99.                                    ])

nan_to_num_ ( nan: float = 0.0, posinf: float | None = None, neginf: float | None = None, name: str | None = None ) → Tensor [source] nan_to_num_¶: Inplace version of nan_to_num API, the output Tensor will be inplaced with input x. Please refer to nan_to_num.

nanmean ( axis: int | Sequence[int] | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] nanmean¶

Compute the arithmetic mean along the specified axis, ignoring NaNs.

Parameters

x (Tensor) – The input Tensor with data type uint16, float16, float32, float64.
axis (int|list|tuple, optional) – The axis along which to perform nanmean calculations. axis should be int, list(int) or tuple(int). If axis is a list/tuple of dimension(s), nanmean is calculated along all element(s) of axis . axis or element(s) of axis should be in range [-D, D), where D is the dimensions of x . If axis or element(s) of axis is less than 0, it works the same way as $axis + D$ . If axis is None, nanmean is calculated over all elements of x. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keepdim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of arithmetic mean along axis of x, with the same data type as x.

Examples

>>> import paddle
>>> # x is a 2-D Tensor:
>>> x = paddle.to_tensor([[float('nan'), 0.3, 0.5, 0.9],
...                       [0.1, 0.2, float('-nan'), 0.7]])
>>> out1 = paddle.nanmean(x)
>>> out1
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
0.44999996)
>>> out2 = paddle.nanmean(x, axis=0)
>>> out2
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.10000000, 0.25000000, 0.50000000, 0.79999995])
>>> out3 = paddle.nanmean(x, axis=0, keepdim=True)
>>> out3
Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.10000000, 0.25000000, 0.50000000, 0.79999995]])
>>> out4 = paddle.nanmean(x, axis=1)
>>> out4
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.56666666, 0.33333334])
>>> out5 = paddle.nanmean(x, axis=1, keepdim=True)
>>> out5
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.56666666],
 [0.33333334]])

>>> # y is a 3-D Tensor:
>>> y = paddle.to_tensor([[[1, float('nan')], [3, 4]],
...                       [[5, 6], [float('-nan'), 8]]])
>>> out6 = paddle.nanmean(y, axis=[1, 2])
>>> out6
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[2.66666675, 6.33333349])
>>> out7 = paddle.nanmean(y, axis=[0, 1])
>>> out7
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[3., 6.])

nanmedian ( axis=None, keepdim=False, mode='avg', name=None ) [source] nanmedian¶

Compute the median along the specified axis, while ignoring NaNs.

If the valid count of elements is a even number, the average value of both elements in the middle is calculated as the median.

Parameters

x (Tensor) – The input Tensor, it’s data type can be int32, int64, float16, bfloat16, float32, float64.
axis (None|int|list|tuple, optional) – The axis along which to perform median calculations axis should be int or list of int. axis should be in range [-D, D), where D is the dimensions of x . If axis is less than 0, it works the same way as $axis + D$. If axis is None, median is calculated over all elements of x. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keepdim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
mode (str, optional) – Whether to use mean or min operation to calculate the nanmedian values when the input tensor has an even number of non-NaN elements along the dimension axis. Support ‘avg’ and ‘min’. Default is ‘avg’.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor or tuple of Tensor. If mode == ‘min’ and axis is int, the result will be a tuple of two tensors (nanmedian value and nanmedian index). Otherwise, only nanmedian value will be returned.

Examples

>>> import paddle
>>> x = paddle.to_tensor([[float('nan'), 2. , 3. ], [0. , 1. , 2. ]])

>>> y1 = x.nanmedian()
>>> print(y1.numpy())
2.0

>>> y2 = x.nanmedian(0)
>>> print(y2.numpy())
[0.  1.5 2.5]

>>> y3 = x.nanmedian(0, keepdim=True)
>>> print(y3.numpy())
[[0.  1.5 2.5]]

>>> y4 = x.nanmedian((0, 1))
>>> print(y4.numpy())
2.0

>>> y5 = x.nanmedian(mode='min')
>>> print(y5.numpy())
2.0

>>> y6, y6_index = x.nanmedian(0, mode='min')
>>> print(y6.numpy())
[0. 1. 2.]
>>> print(y6_index.numpy())
[1 1 1]

>>> y7, y7_index = x.nanmedian(1, mode='min')
>>> print(y7.numpy())
[2. 1.]
>>> print(y7_index.numpy())
[1 1]

>>> y8 = x.nanmedian((0,1), mode='min')
>>> print(y8.numpy())
2.0

nanquantile ( q: float | Sequence[float] | Tensor, axis: list[int] | int | None = None, keepdim: bool = False, interpolation: _Interpolation = 'linear' ) → Tensor [source] nanquantile¶

Compute the quantile of the input as if NaN values in input did not exist. If all values in a reduced row are NaN, then the quantiles for that reduction will be NaN.

Parameters

x (Tensor) – The input Tensor, it’s data type can be float32, float64, int32, int64.
q (int|float|list|Tensor) – The q for calculate quantile, which should be in range [0, 1]. If q is a list or a 1-D Tensor, each element of q will be calculated and the first dimension of output is same to the number of q . If q is a 0-D Tensor, it will be treated as an integer or float.
axis (int|list, optional) – The axis along which to calculate quantile. axis should be int or list of int. axis should be in range [-D, D), where D is the dimensions of x . If axis is less than 0, it works the same way as $axis + D$. If axis is a list, quantile is calculated over all elements of given axes. If axis is None, quantile is calculated over all elements of x. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keepdim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
interpolation (str, optional) – The interpolation method to use when the desired quantile falls between two data points. Must be one of linear, higher, lower, midpoint and nearest. Default is linear.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of quantile along axis of x.

Examples

>>> import paddle

>>> x = paddle.to_tensor(
...     [[0, 1, 2, 3, 4],
...      [5, 6, 7, 8, 9]],
...     dtype="float32")
>>> x[0,0] = float("nan")

>>> y1 = paddle.nanquantile(x, q=0.5, axis=[0, 1])
>>> print(y1)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
5.)

>>> y2 = paddle.nanquantile(x, q=0.5, axis=1)
>>> print(y2)
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[2.50000000, 7.        ])

>>> y3 = paddle.nanquantile(x, q=[0.3, 0.5], axis=0)
>>> print(y3)
Tensor(shape=[2, 5], dtype=float32, place=Place(cpu), stop_gradient=True,
[[5.        , 2.50000000, 3.50000000, 4.50000000, 5.50000000],
 [5.        , 3.50000000, 4.50000000, 5.50000000, 6.50000000]])

>>> y4 = paddle.nanquantile(x, q=0.8, axis=1, keepdim=True)
>>> print(y4)
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[3.40000000],
 [8.20000000]])

>>> nan = paddle.full(shape=[2, 3], fill_value=float("nan"))
>>> y5 = paddle.nanquantile(nan, q=0.8, axis=1, keepdim=True)
>>> print(y5)
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[nan],
 [nan]])

nansum ( axis: int | Sequence[int] | None = None, dtype: DTypeLike | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] nansum¶

Computes the sum of tensor elements over the given axis, treating Not a Numbers (NaNs) as zero.

Parameters

x (Tensor) – An N-D Tensor, the data type is bfloat16, float16, float32, float64, int32 or int64.
axis (int|list|tuple, optional) – The dimensions along which the nansum is performed. If None, nansum all elements of x and return a Tensor with a single element, otherwise must be in the range $[-rank(x), rank(x))$. If $axis[i] < 0$, the dimension to reduce is $rank + axis[i]$.
dtype (str|paddle.dtype|np.dtype, optional) – The dtype of output Tensor. The default value is None, the dtype of output is the same as input Tensor x.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Results of summation operation on the specified axis of input Tensor x,

Return type

Tensor

Examples

>>> import paddle

>>> # x is a Tensor with following elements:
>>> #    [[nan, 0.3, 0.5, 0.9]
>>> #     [0.1, 0.2, -nan, 0.7]]
>>> # Each example is followed by the corresponding output tensor.
>>> x = paddle.to_tensor([[float('nan'), 0.3, 0.5, 0.9],
...                       [0.1, 0.2, float('-nan'), 0.7]],dtype="float32")
>>> out1 = paddle.nansum(x)
>>> out1
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
2.69999981)
>>> out2 = paddle.nansum(x, axis=0)
>>> out2
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.10000000, 0.50000000, 0.50000000, 1.59999990])
>>> out3 = paddle.nansum(x, axis=-1)
>>> out3
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.70000005, 1.        ])
>>> out4 = paddle.nansum(x, axis=1, keepdim=True)
>>> out4
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.70000005],
 [1.        ]])

>>> # y is a Tensor with shape [2, 2, 2] and elements as below:
>>> #      [[[1, nan], [3, 4]],
>>> #       [[5, 6], [-nan, 8]]]
>>> # Each example is followed by the corresponding output tensor.
>>> y = paddle.to_tensor([[[1, float('nan')], [3, 4]],
...                       [[5, 6], [float('-nan'), 8]]])
>>> out5 = paddle.nansum(y, axis=[1, 2])
>>> out5
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[8. , 19.])
>>> out6 = paddle.nansum(y, axis=[0, 1])
>>> out6
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[9. , 18.])

neg ( name: str | None = None ) → Tensor [source] neg¶

This function computes the negative of the Tensor elementwisely.

Parameters

x (Tensor) – Input of neg operator, an N-D Tensor, with data type bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The negative of input Tensor. The shape and data type are the same with input Tensor.

Return type

out (Tensor)

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.neg(x)
>>> out
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 0.40000001,  0.20000000, -0.10000000, -0.30000001])

neg_ ( name: str | None = None ) → Tensor [source] neg_¶: Inplace version of neg API, the output Tensor will be inplaced with input x. Please refer to neg.

negative ( name: str | None = None ) → Tensor [source] negative¶

Returns the negated version of the input Tensor. This is used in Tensor.__neg__, applying the unary - operator to the tensor.

\[Out = -X\]

Parameters

x (Tensor) – The input tensor. The tensor cannot be of type bool.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

A tensor with the same shape and data type as the input tensor. The returned tensor: is the negative.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([-1, 0, 1])
>>> out = paddle.negative(x)
>>> print(out)
Tensor(shape=[3], dtype=int64, place=Place(cpu), stop_gradient=True,
[1,  0,  -1])

nextafter ( y: Tensor, name: str | None = None ) → Tensor [source] nextafter¶

Return the next floating-point value after input towards other, elementwise. The shapes of input and other must be broadcastable.

Parameters

x (Tensor) – An N-D Tensor, the data type is float32, float64.
y (Tensor) – An N-D Tensor, the data type is float32, float64.
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor, the shape and data type is the same with input.

Return type

out (Tensor)

Examples

>>> import paddle
>>> out = paddle.nextafter(paddle.to_tensor([1.0,2.0]),paddle.to_tensor([2.0,1.0]))
>>> out
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.00000012, 1.99999988])

nnz ( ) nnz¶

Note

This API is only available for SparseCooTensor or SparseCsrTensor.

Returns the total number of non zero elements in input SparseCooTensor/SparseCsrTensor.

Returns: int

Examples

>>> import paddle

>>> indices = [[0, 1, 2], [1, 2, 0]]
>>> values = [1.0, 2.0, 3.0]
>>> dense_shape = [3, 3]
>>> coo = paddle.sparse.sparse_coo_tensor(indices, values, dense_shape)
>>> coo.nnz()
3

nonzero ( as_tuple=False ) [source] nonzero¶

Return a tensor containing the indices of all non-zero elements of the input tensor. If as_tuple is True, return a tuple of 1-D tensors, one for each dimension in input, each containing the indices (in that dimension) of all non-zero elements of input. Given a n-Dimensional input tensor with shape [x_1, x_2, …, x_n], If as_tuple is False, we can get a output tensor with shape [z, n], where z is the number of all non-zero elements in the input tensor. If as_tuple is True, we can get a 1-D tensor tuple of length n, and the shape of each 1-D tensor is [z, 1].

Parameters

x (Tensor) – The input tensor variable.
as_tuple (bool, optional) – Return type, Tensor or tuple of Tensor.

Returns

Tensor or tuple of Tensor, The data type is int64.

Examples

>>> import paddle

>>> x1 = paddle.to_tensor([[1.0, 0.0, 0.0],
...                        [0.0, 2.0, 0.0],
...                        [0.0, 0.0, 3.0]])
>>> x2 = paddle.to_tensor([0.0, 1.0, 0.0, 3.0])
>>> out_z1 = paddle.nonzero(x1)
>>> print(out_z1)
Tensor(shape=[3, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0],
 [1, 1],
 [2, 2]])

>>> out_z1_tuple = paddle.nonzero(x1, as_tuple=True)
>>> for out in out_z1_tuple:
...     print(out)
Tensor(shape=[3, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0],
 [1],
 [2]])
Tensor(shape=[3, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0],
 [1],
 [2]])

>>> out_z2 = paddle.nonzero(x2)
>>> print(out_z2)
Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1],
 [3]])

>>> out_z2_tuple = paddle.nonzero(x2, as_tuple=True)
>>> for out in out_z2_tuple:
...     print(out)
Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1],
 [3]])

Returns the matrix norm (the Frobenius norm, the nuclear norm and p-norm) or vector norm (the 1-norm, the Euclidean or 2-norm, and in general the p-norm) of a given tensor.

Whether the function calculates the vector norm or the matrix norm is determined as follows:

If axis is of type int, calculate the vector norm.
If axis is a two-dimensional array, calculate the matrix norm.
If axis is None, x is compressed into a one-dimensional vector and the vector norm is calculated.

Paddle supports the following norms:

porder	norm for matrices	norm for vectors
None(default)	frobenius norm	2_norm
fro	frobenius norm	not support
nuc	nuclear norm	not support
inf	max(sum(abs(x), dim=1))	max(abs(x))
-inf	min(sum(abs(x), dim=1))	min(abs(x))
0	not support	sum(x != 0)
1	max(sum(abs(x), dim=0))	as below
-1	min(sum(abs(x), dim=0))	as below
2	The maximum singular value of a matrix consisting of axis.	as below
-2	The minimum singular value of a matrix consisting of axis.	as below
other int or float	not support	sum(abs(x)^{porder})^ {(1 / porder)}

Parameters

x (Tensor) – The input tensor could be N-D tensor, and the input data type could be float32 or float64.
p (int|float|string|None, optional) – Order of the norm. Supported values are fro, nuc, 0, ±1, ±2, ±inf and any real number yielding the corresponding p-norm. Default value is None.
axis (int|list|tuple, optional) – The axis on which to apply norm operation. If axis is int or list(int)/tuple(int) with only one element, the vector norm is computed over the axis. If axis < 0, the dimension to norm operation is rank(input) + axis. If axis is a list(int)/tuple(int) with two elements, the matrix norm is computed over the axis. Default value is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have fewer dimension than the input unless keepdim is true, default value is False.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

results of norm operation on the specified axis of input tensor, it’s data type is the same as input’s Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.arange(24, dtype="float32").reshape([2, 3, 4]) - 12
>>> print(x)
Tensor(shape=[2, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[-12., -11., -10., -9. ],
  [-8. , -7. , -6. , -5. ],
  [-4. , -3. , -2. , -1. ]],
 [[ 0. ,  1. ,  2. ,  3. ],
  [ 4. ,  5. ,  6. ,  7. ],
  [ 8. ,  9. ,  10.,  11.]]])

>>> # compute frobenius norm along last two dimensions.
>>> out_fro = paddle.linalg.norm(x, p='fro', axis=[0,1])
>>> print(out_fro)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[17.43559647, 16.91153526, 16.73320007, 16.91153526])

>>> # compute 2-order vector norm along last dimension.
>>> out_pnorm = paddle.linalg.norm(x, p=2, axis=-1)
>>> print(out_pnorm)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[21.11871147, 13.19090557, 5.47722578 ],
 [3.74165750 , 11.22497177, 19.13112640]])

>>> # compute 2-order  norm along [0,1] dimension.
>>> out_pnorm = paddle.linalg.norm(x, p=2, axis=[0,1])
>>> print(out_pnorm)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[15.75857544, 14.97978878, 14.69693947, 14.97978973])

>>> # compute inf-order  norm
>>> out_pnorm = paddle.linalg.norm(x, p=float("inf"))
>>> print(out_pnorm)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
12.)

>>> out_pnorm = paddle.linalg.norm(x, p=float("inf"), axis=0)
>>> print(out_pnorm)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[12., 11., 10., 9. ],
 [8. , 7. , 6. , 7. ],
 [8. , 9. , 10., 11.]])

>>> # compute -inf-order  norm
>>> out_pnorm = paddle.linalg.norm(x, p=-float("inf"))
>>> print(out_pnorm)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
0.)

>>> out_pnorm = paddle.linalg.norm(x, p=-float("inf"), axis=0)
>>> print(out_pnorm)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 1., 2., 3.],
 [4., 5., 6., 5.],
 [4., 3., 2., 1.]])

normal_ ( mean: complex = 0.0, std: float = 1.0, name: str | None = None ) → Tensor [source] normal_¶

This is the inplace version of api normal, which returns a Tensor filled with random values sampled from a normal distribution. The output Tensor will be inplaced with input x. Please refer to normal.

Parameters

x (Tensor) – The input tensor to be filled with random values.
mean (float|int|complex, optional) – Mean of the output tensor, default is 0.0.
std (float|int, optional) – Standard deviation of the output tensor, default is 1.0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, A Tensor filled with random values sampled from a normal distribution with mean and std .

Examples

>>> import paddle
>>> x = paddle.randn([3, 4])
>>> x.normal_()
>>> 
>>> print(x)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 0.06132207,  1.11349595,  0.41906244, -0.24858207],
 [-1.85169315, -1.50370061,  1.73954511,  0.13331604],
 [ 1.66359663, -0.55764782, -0.59911072, -0.57773495]])

not_equal ( y: Tensor, name: str | None = None ) → Tensor [source] not_equal¶

Returns the truth value of $x != y$ elementwise, which is equivalent function to the overloaded operator !=.

Note

The output has no gradient.

Parameters

x (Tensor) – First input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
y (Tensor) – Second input to compare which is N-D tensor. The input data type should be bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The output shape is same as input x. The output data type is bool.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = paddle.to_tensor([1, 3, 2])
>>> result1 = paddle.not_equal(x, y)
>>> print(result1)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[False, True , True ])

not_equal_ ( y: Tensor, name: str | None = None ) → Tensor [source] not_equal_¶: Inplace version of not_equal API, the output Tensor will be inplaced with input x. Please refer to not_equal.

num_shard

Tensor’s num_shard.

Returns: Tensor’s num_shard.
Return type: int64_t

Examples

>>> 
>>> import paddle
>>> import paddle.distributed as dist
>>> from paddle.base import core

>>> mesh = dist.ProcessMesh([[2, 4, 5], [0, 1, 3]], dim_names=["x", "y"])

>>> a = paddle.to_tensor([[1,2,3],
...                       [5,6,7]])
>>> d_tensor = paddle.Tensor(a, [core.Shard(0), core.Shard(1)])

>>> print(d_tensor.num_shard) # 4

numel ( name: str | None = None ) → Tensor [source] numel¶

Returns the number of elements for a tensor, which is a 0-D int64 Tensor with shape [].

Parameters

x (Tensor) – The input Tensor, it’s data type can be bool, float16, float32, float64, uint8, int8, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The number of elements for the input Tensor, whose shape is [].

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.full(shape=[4, 5, 7], fill_value=0, dtype='int32')
>>> numel = paddle.numel(x)
>>> print(numel.numpy())
140

numpy ( ) numpy¶

Returns a numpy array shows the value of current Tensor.

Returns: ndarray, The numpy value of current Tensor, dtype is same as current Tensor.

Examples

>>> import paddle
>>> x = paddle.to_tensor([[1.0, 2.0, 3.0],
...                       [4.0, 5.0, 6.0]])
>>> x.numpy()
array([[1., 2., 3.],
       [4., 5., 6.]], dtype=float32)

offset

The address of the first element relative to the offset of the video memory.

Returns: offset.
Return type: int

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = x[1]
>>> print(y.offset)
8

ormqr ( tau: Tensor, y: Tensor, left: bool = True, transpose: bool = False, name: str | None = None ) → Tensor ormqr¶

Calculate the product of a normal matrix and a householder matrix. Compute the product of the matrix C (given by y) with dimensions (m, n) and a matrix Q, where Q is generated by the Householder reflection coefficient (x, tau). Returns a Tensor.

Parameters

x (Tensor) – Shape(*,mn, k), when left is True, the value of mn is equal to m, otherwise the value of mn is equal to n. * indicates that the length of the tensor on axis 0 is 0 or greater.
tau (Tensor) – Shape (*, min(mn, k)), where * indicates that the length of the Tensor on axis 0 is 0 or greater, and its type is the same as input.
y (Tensor) – Shape (*m,n), where * indicates that the length of the Tensor on axis 0 is 0 or greater, and its type is the same as input.
left (bool, optional) – Determines the order in which the matrix product operations are operated. If left is true, the order of evaluation is op(Q) * y, otherwise, the order of evaluation is y * op(Q). Default value: True.
transpose (bool, optional) – If true, the matrix Q is conjugated and transposed, otherwise, the conjugate transpose transformation is not performed. Default value: False.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor. Data type and dimension are equals with y.

Examples

>>> import paddle
>>> import numpy as np
>>> from paddle import  linalg

>>> input = paddle.to_tensor([[-114.6, 10.9, 1.1], [-0.304, 38.07, 69.38], [-0.45, -0.17, 62]])
>>> tau = paddle.to_tensor([1.55, 1.94, 3.0])
>>> y = paddle.to_tensor([[-114.6, 10.9, 1.1], [-0.304, 38.07, 69.38], [-0.45, -0.17, 62]])
>>> output = linalg.ormqr(input, tau, y)
>>> print(output)
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
    [[ 63.82712936 , -13.82312393 , -116.28614044],
    [-53.65926361 , -28.15783691 , -70.42700958 ],
    [-79.54292297 ,  24.00182915 , -41.34253311 ]])

outer ( y: Tensor, name: str | None = None ) → Tensor [source] outer¶

Outer product of two Tensors.

Input is flattened if not already 1-dimensional.

Parameters

x (Tensor) – An N-D Tensor or a Scalar Tensor.
y (Tensor) – An N-D Tensor or a Scalar Tensor.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The outer-product Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> x = paddle.arange(1, 4).astype('float32')
>>> y = paddle.arange(1, 6).astype('float32')
>>> out = paddle.outer(x, y)
>>> print(out)
Tensor(shape=[3, 5], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1. , 2. , 3. , 4. , 5. ],
 [2. , 4. , 6. , 8. , 10.],
 [3. , 6. , 9. , 12., 15.]])

pca_lowrank ( q: int | None = None, center: bool = True, niter: int = 2, name: str | None = None ) → tuple[Tensor, Tensor, Tensor] pca_lowrank¶

Performs linear Principal Component Analysis (PCA) on a low-rank matrix or batches of such matrices.

Let $X$ be the input matrix or a batch of input matrices, the output should satisfies:

\[X = U * diag(S) * V^{T}\]

Parameters

x (Tensor) – The input tensor. Its shape should be […, N, M], where … is zero or more batch dimensions. N and M can be arbitrary positive number. The data type of x should be float32 or float64.
q (int, optional) – a slightly overestimated rank of $X$. Default value is $q=min(6,N,M)$.
center (bool, optional) – if True, center the input tensor. Default value is True.
niter (int, optional) – number of iterations to perform. Default: 2.
name (str|None, optional) – Name for the operation. For more information, please refer to Name. Default: None.

Returns

Tensor U, is N x q matrix.
Tensor S, is a vector with length q.
Tensor V, is M x q matrix.

tuple (U, S, V): which is the nearly optimal approximation of a singular value decomposition of a centered matrix $X$.

Examples

 >>> import paddle
 >>> paddle.seed(2023)

 >>> x = paddle.randn((5, 5), dtype='float64')
 >>> U, S, V = paddle.linalg.pca_lowrank(x)
 >>> print(U)
Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True,
[[ 0.80131563,  0.11962647,  0.27667179, -0.25891214,  0.44721360],
 [-0.12642301,  0.69917551, -0.17899393,  0.51296394,  0.44721360],
 [ 0.08997135, -0.69821706, -0.20059228,  0.51396579,  0.44721360],
 [-0.23871837, -0.02815453, -0.59888153, -0.61932365,  0.44721360],
 [-0.52614559, -0.09243040,  0.70179595, -0.14869394,  0.44721360]])

 >>> print(S)
 Tensor(shape=[5], dtype=float64, place=Place(cpu), stop_gradient=True,
 [2.60101614, 2.40554940, 1.49768346, 0.19064830, 0.00000000])

 >>> print(V)
 Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True,
 [[ 0.58339481, -0.17143771,  0.00522143,  0.57976310,  0.54231640],
  [ 0.22334335,  0.72963474, -0.30148399, -0.39388750,  0.41438019],
  [ 0.05416913,  0.34666487,  0.93549758,  0.00063507,  0.04162998],
  [-0.39519094,  0.53074980, -0.16687419,  0.71175586, -0.16638919],
  [-0.67131070, -0.19071018,  0.07795789, -0.04615811,  0.71046714]])

persistable

Tensor’s persistable.

Returns: persistable.
Return type: bool

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.0, stop_gradient=False)
>>> print(x.persistable)
False

>>> x. persistable = True
>>> print(x.persistable)
True

pinv ( rcond: float | Tensor = 1e-15, hermitian: bool = False, name: str | None = None ) → Tensor pinv¶

Calculate pseudo inverse via SVD(singular value decomposition) of one matrix or batches of regular matrix.

\[if hermitian == False: x = u * s * vt (SVD) out = v * 1/s * ut else: x = u * s * ut (eigh) out = u * 1/s * u.conj().transpose(-2,-1)\]

If x is hermitian or symmetric matrix, svd will be replaced with eigh.

Parameters

x (Tensor) – The input tensor. Its shape should be (*, m, n) where * is zero or more batch dimensions. m and n can be arbitrary positive number. The data type of x should be float32 or float64 or complex64 or complex128. When data type is complex64 or complex128, hermitian should be set True.
rcond (Tensor|float, optional) – the tolerance value to determine when is a singular value zero. Default:1e-15.
hermitian (bool, optional) – indicates whether x is Hermitian if complex or symmetric if real. Default: False.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The tensor with same data type with x. it represents pseudo inverse of x. Its shape should be (*, n, m).

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.arange(15).reshape((3, 5)).astype('float64')
>>> input = paddle.to_tensor(x)
>>> out = paddle.linalg.pinv(input)
>>> print(input)
Tensor(shape=[3, 5], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0. , 1. , 2. , 3. , 4. ],
 [5. , 6. , 7. , 8. , 9. ],
 [10., 11., 12., 13., 14.]])

>>> print(out)
Tensor(shape=[5, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[-0.22666667, -0.06666667,  0.09333333],
 [-0.12333333, -0.03333333,  0.05666667],
 [-0.02000000, -0.00000000,  0.02000000],
 [ 0.08333333,  0.03333333, -0.01666667],
 [ 0.18666667,  0.06666667, -0.05333333]])

# one can verify : x * out * x = x ;
# or              out * x * out = x ;

place

The device Tensor’s memory locate.

Returns: place.
Return type: Place

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> print(x.place)
Place(cpu)

placements

Get placements property from shard tensor.

Returns: the process mesh of shard tensor
Return type: List[core.Placement]

Examples

>>> 
>>> import paddle
>>> import paddle.distributed as dist
>>> from paddle.base import core

>>> mesh = dist.ProcessMesh([[2, 4, 5], [0, 1, 3]], dim_names=["x", "y"])

>>> a = paddle.to_tensor([[1,2,3],
...                       [5,6,7]])
>>> d_tensor = dist.shard_tensor(a, mesh, [core.Shard(0), core.Shard(1)])

>>> print(d_tensor.placements)

polar ( angle: Tensor, name: Optional[str] = None ) → Tensor [source] polar¶

Return a Cartesian coordinates corresponding to the polar coordinates complex tensor given the abs and angle component.

Parameters

abs (Tensor) – The abs component. The data type should be ‘float32’ or ‘float64’.
angle (Tensor) – The angle component. The data type should be the same as abs.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, The output tensor. The data type is ‘complex64’ or ‘complex128’, with the same precision as abs and angle.

Note

paddle.polar supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Examples

>>> import paddle
>>> import numpy as np

>>> abs = paddle.to_tensor([1, 2], dtype=paddle.float64)
>>> angle = paddle.to_tensor([np.pi / 2, 5 * np.pi / 4], dtype=paddle.float64)
>>> out = paddle.polar(abs, angle)
>>> print(out)
Tensor(shape=[2], dtype=complex128, place=Place(cpu), stop_gradient=True,
[ (6.123233995736766e-17+1j)             ,
 (-1.4142135623730954-1.414213562373095j)])

polygamma ( n: int, name: str | None = None ) → Tensor [source] polygamma¶

Calculates the polygamma of the given input tensor, element-wise.

The equation is:

\[\Phi^n(x) = \frac{d^n}{dx^n} [\ln(\Gamma(x))]\]

Parameters

x (Tensor) – Input Tensor. Must be one of the following types: float32, float64, uint8, int8, int16, int32, int64.
n (int) – Order of the derivative. Must be integral.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), A Tensor. the polygamma of the input Tensor, the shape and data type is the same with input

(integer types are autocasted into float32).

Examples

>>> import paddle

>>> data = paddle.to_tensor([2, 3, 25.5], dtype='float32')
>>> res = paddle.polygamma(data, 1)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.64493412,  0.39493406,  0.03999467])

polygamma_ ( n: int, name: str | None = None ) → Tensor [source] polygamma_¶: Inplace version of polygamma API, the output Tensor will be inplaced with input x. Please refer to polygamma.

pow ( y: float | Tensor, name: str | None = None ) → Tensor [source] pow¶

Compute the power of Tensor elements. The equation is:

\[out = x^{y}\]

Note

paddle.pow supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – An N-D Tensor, the data type is bfloat16, float16, float32, float64, int32, int64, complex64 or complex128.
y (float|int|Tensor) – If it is an N-D Tensor, its data type should be the same as x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. Its dimension and data type are the same as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3], dtype='float32')

>>> # example 1: y is a float or int
>>> res = paddle.pow(x, 2)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1., 4., 9.])
>>> res = paddle.pow(x, 2.5)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.         , 5.65685415 , 15.58845711])

>>> # example 2: y is a Tensor
>>> y = paddle.to_tensor([2], dtype='float32')
>>> res = paddle.pow(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1., 4., 9.])

pow_ ( y: float | Tensor, name: str | None = None ) → Tensor [source] pow_¶: Inplace version of pow API, the output Tensor will be inplaced with input x. Please refer to pow.

process_mesh

Get process_mesh property from shard tensor.

Returns: the process mesh of shard tensor
Return type: core.ProcessMesh

Examples

>>> 
>>> import paddle
>>> import paddle.distributed as dist
>>> from paddle.base import core

>>> mesh = dist.ProcessMesh([[2, 4, 5], [0, 1, 3]], dim_names=["x", "y"])

>>> a = paddle.to_tensor([[1,2,3],
...                       [5,6,7]])
>>> d_tensor = dist.shard_tensor(a, mesh, [core.Shard(0), core.Shard(1)])

>>> print(d_tensor.process_mesh)

prod ( axis: int | Sequence[int] | None = None, keepdim: bool = False, dtype: DTypeLike | None = None, name: str | None = None ) → Tensor [source] prod¶

Compute the product of tensor elements over the given axis.

Parameters

x (Tensor) – The input tensor, its data type should be bfloat16, float16, float32, float64, int32, int64, complex64, complex128.
axis (int|list|tuple|None, optional) – The axis along which the product is computed. If None, multiply all elements of x and return a Tensor with a single element, otherwise must be in the range $[-x.ndim, x.ndim)$. If $axis[i]<0$, the axis to reduce is $x.ndim + axis[i]$. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the input unless keepdim is true. Default is False.
dtype (str|paddle.dtype|np.dtype, optional) – The desired date type of returned tensor, can be bfloat16, float16, float32, float64, int32, int64. If specified, the input tensor is casted to dtype before operator performed. This is very useful for avoiding data type overflows. The default value is None, the dtype of output is the same as input Tensor x.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, result of product on the specified dim of input tensor.

Examples

>>> import paddle

>>> # the axis is a int element
>>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9],
...                       [0.1, 0.2, 0.6, 0.7]])
>>> out1 = paddle.prod(x)
>>> out1
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
0.00022680)

>>> out2 = paddle.prod(x, -1)
>>> out2
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.02700000, 0.00840000])

>>> out3 = paddle.prod(x, 0)
>>> out3
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.02000000, 0.06000000, 0.30000001, 0.63000000])

>>> out4 = paddle.prod(x, 0, keepdim=True)
>>> out4
Tensor(shape=[1, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.02000000, 0.06000000, 0.30000001, 0.63000000]])

>>> out5 = paddle.prod(x, 0, dtype='int64')
>>> out5
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 0, 0, 0])

>>> # the axis is list
>>> y = paddle.to_tensor([[[1.0, 2.0], [3.0, 4.0]],
...                         [[5.0, 6.0], [7.0, 8.0]]])
>>> out6 = paddle.prod(y, [0, 1])
>>> out6
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[105., 384.])

>>> out7 = paddle.prod(y, (1, 2))
>>> out7
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[24.  , 1680.])

put_along_axis ( indices: Tensor, values: float | Tensor, axis: int, reduce: Literal['assign', 'add', 'mul', 'multiply', 'mean', 'amin', 'amax'] = 'assign', include_self: bool = True, broadcast: bool = True ) → Tensor [source] put_along_axis¶

Put values into the destination array by given indices matrix along the designated axis.

Parameters

arr (Tensor) – The Destination Tensor. Supported data types are bfloat16, float16, float32, float64, int32, int64, uint8.
indices (Tensor) – Indices to put along each 1d slice of arr. This must match the dimension of arr, and need to broadcast against arr if broadcast is ‘True’. Supported data type are int32 and int64.
values (scalar|Tensor) – The value element(s) to put. The data types should be same as arr.
axis (int) – The axis to put 1d slices along.
reduce (str, optional) – The reduce operation, default is ‘assign’, support ‘add’, ‘assign’, ‘mul’, ‘multiply’, ‘mean’, ‘amin’ and ‘amax’.
include_self (bool, optional) – whether to reduce with the elements of arr, default is ‘True’.
broadcast (bool, optional) – whether to broadcast indices, default is ‘True’.

Returns

Tensor, The indexed element, same dtype with arr

Examples

>>> import paddle

>>> x = paddle.to_tensor([[10, 30, 20], [60, 40, 50]])
>>> index = paddle.to_tensor([[0]])
>>> value = 99
>>> axis = 0
>>> result = paddle.put_along_axis(x, index, value, axis)
>>> print(result)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[99, 99, 99],
 [60, 40, 50]])

>>> index = paddle.zeros((2,2)).astype("int32")
>>> value=paddle.to_tensor([[1,2],[3,4]]).astype(x.dtype)
>>> result = paddle.put_along_axis(x, index, value, 0, "add", True, False)
>>> print(result)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[14, 36, 20],
 [60, 40, 50]])

>>> result = paddle.put_along_axis(x, index, value, 0, "mul", True, False)
>>> print(result)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[30 , 240, 20 ],
 [60 , 40 , 50 ]])

>>> result = paddle.put_along_axis(x, index, value, 0, "mean", True, False)
>>> print(result)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[4 , 12, 20],
 [60, 40, 50]])

>>> result = paddle.put_along_axis(x, index, value, 0, "amin", True, False)
>>> print(result)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 20],
 [60, 40, 50]])

>>> result = paddle.put_along_axis(x, index, value, 0, "amax", True, False)
>>> print(result)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[10, 30, 20],
 [60, 40, 50]])

>>> result = paddle.put_along_axis(x, index, value, 0, "add", False, False)
>>> print(result)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[4 , 6 , 20],
 [60, 40, 50]])

put_along_axis_ ( indices: Tensor, values: float | Tensor, axis: int, reduce: Literal['assign', 'add', 'mul', 'multiply', 'mean', 'amin', 'amax'] = 'assign', include_self: bool = True, broadcast: bool = True ) put_along_axis_¶: Inplace version of put_along_axis API, the output Tensor will be inplaced with input arr. Please refer to put_along_axis.

qr ( mode='reduced', name=None ) → Tensor | tuple[Tensor, Tensor] qr¶

Computes the QR decomposition of one matrix or batches of matrices (backward is unsupported now).

Parameters

x (Tensor) – The input tensor. Its shape should be […, M, N], where … is zero or more batch dimensions. M and N can be arbitrary positive number. The data type of x supports float, double, complex64, complex128.
mode (str, optional) – A flag to control the behavior of qr. Suppose x’s shape is […, M, N] and denoting K = min(M, N): If mode = “reduced”, qr op will return reduced Q and R matrices, which means Q’s shape is […, M, K] and R’s shape is […, K, N]. If mode = “complete”, qr op will return complete Q and R matrices, which means Q’s shape is […, M, M] and R’s shape is […, M, N]. If mode = “r”, qr op will only return reduced R matrix, which means R’s shape is […, K, N]. Default: “reduced”.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

If mode = “reduced” or mode = “complete”, qr will return a two tensor-tuple, which represents Q and R. If mode = “r”, qr will return a tensor which represents R.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]]).astype('float64')
>>> q, r = paddle.linalg.qr(x)
>>> print(q)
Tensor(shape=[3, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[-0.16903085,  0.89708523],
 [-0.50709255,  0.27602622],
 [-0.84515425, -0.34503278]])
>>> print(r)
Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[-5.91607978, -7.43735744],
 [ 0.        ,  0.82807867]])

>>> # one can verify : X = Q * R ;

quantile ( q: float | Sequence[float] | Tensor, axis: int | list[int] | None = None, keepdim: bool = False, interpolation: _Interpolation = 'linear' ) → Tensor [source] quantile¶

Compute the quantile of the input along the specified axis. If any values in a reduced row are NaN, then the quantiles for that reduction will be NaN.

Parameters

x (Tensor) – The input Tensor, it’s data type can be float32, float64, int32, int64.
q (int|float|list|Tensor) – The q for calculate quantile, which should be in range [0, 1]. If q is a list or a 1-D Tensor, each element of q will be calculated and the first dimension of output is same to the number of q . If q is a 0-D Tensor, it will be treated as an integer or float.
axis (int|list, optional) – The axis along which to calculate quantile. axis should be int or list of int. axis should be in range [-D, D), where D is the dimensions of x . If axis is less than 0, it works the same way as $axis + D$. If axis is a list, quantile is calculated over all elements of given axes. If axis is None, quantile is calculated over all elements of x. Default is None.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keepdim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
interpolation (str, optional) – The interpolation method to use when the desired quantile falls between two data points. Must be one of linear, higher, lower, midpoint and nearest. Default is linear.
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of quantile along axis of x.

Examples

>>> import paddle

>>> y = paddle.arange(0, 8 ,dtype="float32").reshape([4, 2])
>>> print(y)
Tensor(shape=[4, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 1.],
 [2., 3.],
 [4., 5.],
 [6., 7.]])

>>> y1 = paddle.quantile(y, q=0.5, axis=[0, 1])
>>> print(y1)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
3.50000000)

>>> y2 = paddle.quantile(y, q=0.5, axis=1)
>>> print(y2)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.50000000, 2.50000000, 4.50000000, 6.50000000])

>>> y3 = paddle.quantile(y, q=[0.3, 0.5], axis=0)
>>> print(y3)
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.80000000, 2.80000000],
 [3.        , 4.        ]])

>>> y[0,0] = float("nan")
>>> y4 = paddle.quantile(y, q=0.8, axis=1, keepdim=True)
>>> print(y4)
Tensor(shape=[4, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[nan       ],
 [2.80000000],
 [4.80000000],
 [6.80000000]])

rad2deg ( name: str | None = None ) → Tensor [source] rad2deg¶

Convert each of the elements of input x from angles in radians to degrees.

Equation:: \[rad2deg(x)=180/ \pi * x\]

Parameters

x (Tensor) – An N-D Tensor, the data type is float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

An N-D Tensor, the shape and data type is the same with input (The output data type is float32 when the input data type is int).

Return type

out (Tensor)

Examples

>>> import paddle
>>> import math

>>> x1 = paddle.to_tensor([3.142, -3.142, 6.283, -6.283, 1.570, -1.570])
>>> result1 = paddle.rad2deg(x1)
>>> result1
Tensor(shape=[6], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 180.02334595, -180.02334595,  359.98937988, -359.98937988,
  89.95437622 , -89.95437622 ])

>>> x2 = paddle.to_tensor(math.pi/2)
>>> result2 = paddle.rad2deg(x2)
>>> result2
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
90.)

>>> x3 = paddle.to_tensor(1)
>>> result3 = paddle.rad2deg(x3)
>>> result3
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
57.29578018)

rank ( ) → Tensor [source] rank¶

Returns the number of dimensions for a tensor, which is a 0-D int32 Tensor.

Parameters: input (Tensor) – The input Tensor with shape of $[N_1, N_2, ..., N_k]$, the data type is arbitrary.
Returns: The 0-D tensor with the dimensions of the input Tensor.
Return type: Tensor, the output data type is int32.

Examples

>>> import paddle

>>> input = paddle.rand((3, 100, 100))
>>> rank = paddle.rank(input)
>>> print(rank.numpy())
3

real ( name: str | None = None ) → Tensor [source] real¶

Returns a new Tensor containing real values of the input Tensor.

Parameters

x (Tensor) – the input Tensor, its data type could be complex64 or complex128.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

a Tensor containing real values of the input Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor(
...     [[1 + 6j, 2 + 5j, 3 + 4j], [4 + 3j, 5 + 2j, 6 + 1j]])
>>> print(x)
Tensor(shape=[2, 3], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[(1+6j), (2+5j), (3+4j)],
 [(4+3j), (5+2j), (6+1j)]])

>>> real_res = paddle.real(x)
>>> print(real_res)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 2., 3.],
 [4., 5., 6.]])

>>> real_t = x.real()
>>> print(real_t)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 2., 3.],
 [4., 5., 6.]])

reciprocal ( name: str | None = None ) → Tensor [source] reciprocal¶

Reciprocal Activation Operator.

\[out = \frac{1}{x}\]

Parameters

x (Tensor) – Input of Reciprocal operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Reciprocal operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.reciprocal(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-2.50000000, -5.        ,  10.       ,  3.33333325])

reciprocal_ ( name=None ) reciprocal_¶: Inplace version of reciprocal API, the output Tensor will be inplaced with input x. Please refer to reciprocal.

reconstruct_from_ ( other ) reconstruct_from_¶

Reconstruct the self with other Tensor. It is a deep copy of ‘self = other’.

Returns: None.

Examples

>>> import paddle

>>> t1 = paddle.to_tensor([1.0], stop_gradient=False)
>>> t2 = paddle.to_tensor([2.0], stop_gradient=True)

>>> t1.reconstruct_from_(t2)
>>> print(t1)
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True, [2.])

reduce_as ( target: Tensor, name: str | None = None ) → Tensor [source] reduce_as¶

Computes the sum of tensor elements make the shape of its result equal to the shape of target.

Parameters

x (Tensor) – An N-D Tensor, the data type is bool, float16, float32, float64, int8, uint8, int16, uint16, int32, int64, complex64 or complex128.
target (Tensor) – An N-D Tensor, the length of x shape must greater than or equal to the length of target shape. The data type is bool, float16, float32, float64, int8, uint8, int16, uint16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The sum of the input tensor x along some axis has the same shape as the shape of the input tensor target, if x.dtype=’bool’, x.dtype=’int32’, it’s data type is ‘int64’, otherwise it’s data type is the same as x.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2, 3, 4], [5, 6, 7, 8]])
>>> x
Tensor(shape=[2, 4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
[[1, 2, 3, 4],
 [5, 6, 7, 8]])
>>> target = paddle.to_tensor([1, 2, 3, 4])
>>> target
Tensor(shape=[4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
[1, 2, 3, 4])
>>> res = paddle.reduce_as(x, target)
>>> res
Tensor(shape=[4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
[6 , 8 , 10, 12])

register_hook ( hook: Callable[[Tensor], Tensor | None] ) → TensorHookRemoveHelper register_hook¶

Registers a backward hook for current Tensor.

The hook will be called every time the gradient Tensor of current Tensor is computed.

The hook should not modify the input gradient Tensor, but it can optionally return a new gradient Tensor which will be used in place of current Tensor’s gradient.

The hook should have the following signature:

hook(grad) -> Tensor or None

Parameters: hook (function) – A backward hook to be registered for Tensor.grad
Returns: A helper object that can be used to remove the registered hook by calling remove() method.
Return type: TensorHookRemoveHelper

Examples

>>> import paddle

>>> # hook function return None
>>> def print_hook_fn(grad):
...     print(grad)
...
>>> # hook function return Tensor
>>> def double_hook_fn(grad):
...     grad = grad * 2
...     return grad
...
>>> x = paddle.to_tensor([0., 1., 2., 3.], stop_gradient=False)
>>> y = paddle.to_tensor([4., 5., 6., 7.], stop_gradient=False)
>>> z = paddle.to_tensor([1., 2., 3., 4.])

>>> # one Tensor can register multiple hooks
>>> h = x.register_hook(print_hook_fn)
>>> x.register_hook(double_hook_fn)

>>> w = x + y
>>> # register hook by lambda function
>>> w.register_hook(lambda grad: grad * 2)

>>> o = z.matmul(w)
>>> o.backward()
>>> # print_hook_fn print content in backward
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=False,
[2., 4., 6., 8.])

>>> print("w.grad:", w.grad)
w.grad: None
>>> print("x.grad:", x.grad)
x.grad: Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=False,
[4. , 8. , 12., 16.])
>>> print("y.grad:", y.grad)
y.grad: Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=False,
[2., 4., 6., 8.])

>>> # remove hook
>>> h.remove()

remainder ( y: Tensor, name: str | None = None ) → Tensor [source] remainder¶

Mod two tensors element-wise. The equation is:

\[out = x \% y\]

Note

paddle.remainder supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

And mod, floor_mod are all functions with the same name

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 8, 7])
>>> y = paddle.to_tensor([1, 5, 3, 3])
>>> z = paddle.remainder(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

>>> z = paddle.floor_mod(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

>>> z = paddle.mod(x, y)
>>> print(z)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 3, 2, 1])

remainder_ ( y: Tensor, name: str | None = None ) → Tensor [source] remainder_¶: Inplace version of floor_mod_ API, the output Tensor will be inplaced with input x. Please refer to floor_mod_.

renorm ( p: float, axis: int, max_norm: float ) → Tensor [source] renorm¶

renorm

This operator is used to calculate the p-norm along the axis, suppose the input-shape on axis dimension has the value of T, then the tensor is split into T parts, the p-norm should be calculated for each part, if the p-norm for part i is larger than max-norm, then each element in part i should be re-normalized at the same scale so that part-i’ p-norm equals max-norm exactly, otherwise part-i stays unchanged.

Parameters

x (Tensor) – The input Tensor
p (float) – The power of the norm operation.
axis (int) – the dimension to slice the tensor.
max-norm (float) – the maximal norm limit.

Returns

the renorm Tensor.

Return type

Tensor

Examples

>>> import paddle
>>> input = [[[2.0, 2.0, -2.0], [3.0, 0.3, 3.0]],
...          [[2.0, -8.0, 2.0], [3.1, 3.7, 3.0]]]
>>> x = paddle.to_tensor(input,dtype='float32')
>>> y = paddle.renorm(x, 1.0, 2, 2.05)
>>> print(y)
Tensor(shape=[2, 2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[ 0.40594056,  0.29285714, -0.41000000],
  [ 0.60891086,  0.04392857,  0.61500001]],
 [[ 0.40594056, -1.17142856,  0.41000000],
  [ 0.62920785,  0.54178572,  0.61500001]]])

renorm_ ( p: float, axis: int, max_norm: float ) → Tensor [source] renorm_¶: Inplace version of renorm API, the output Tensor will be inplaced with input x. Please refer to renorm.

repeat_interleave ( repeats: int | Tensor, axis: int | None = None, name: str | None = None ) → Tensor [source] repeat_interleave¶

Returns a new tensor which repeats the x tensor along dimension axis using the entries in repeats which is a int or a Tensor.

The image illustrates a typical case of the repeat_interleave operation. Given a tensor [[1, 2, 3], [4, 5, 6]], with the repeat counts repeats = [3, 2, 1] and parameter axis = 1, it means that the elements in the 1st column are repeated 3 times, the 2nd column is repeated 2 times, and the 3rd column is repeated 1 time.

The final output is a 2D tensor: [[1, 1, 1, 2, 2, 3], [4, 4, 4, 5, 5, 6]].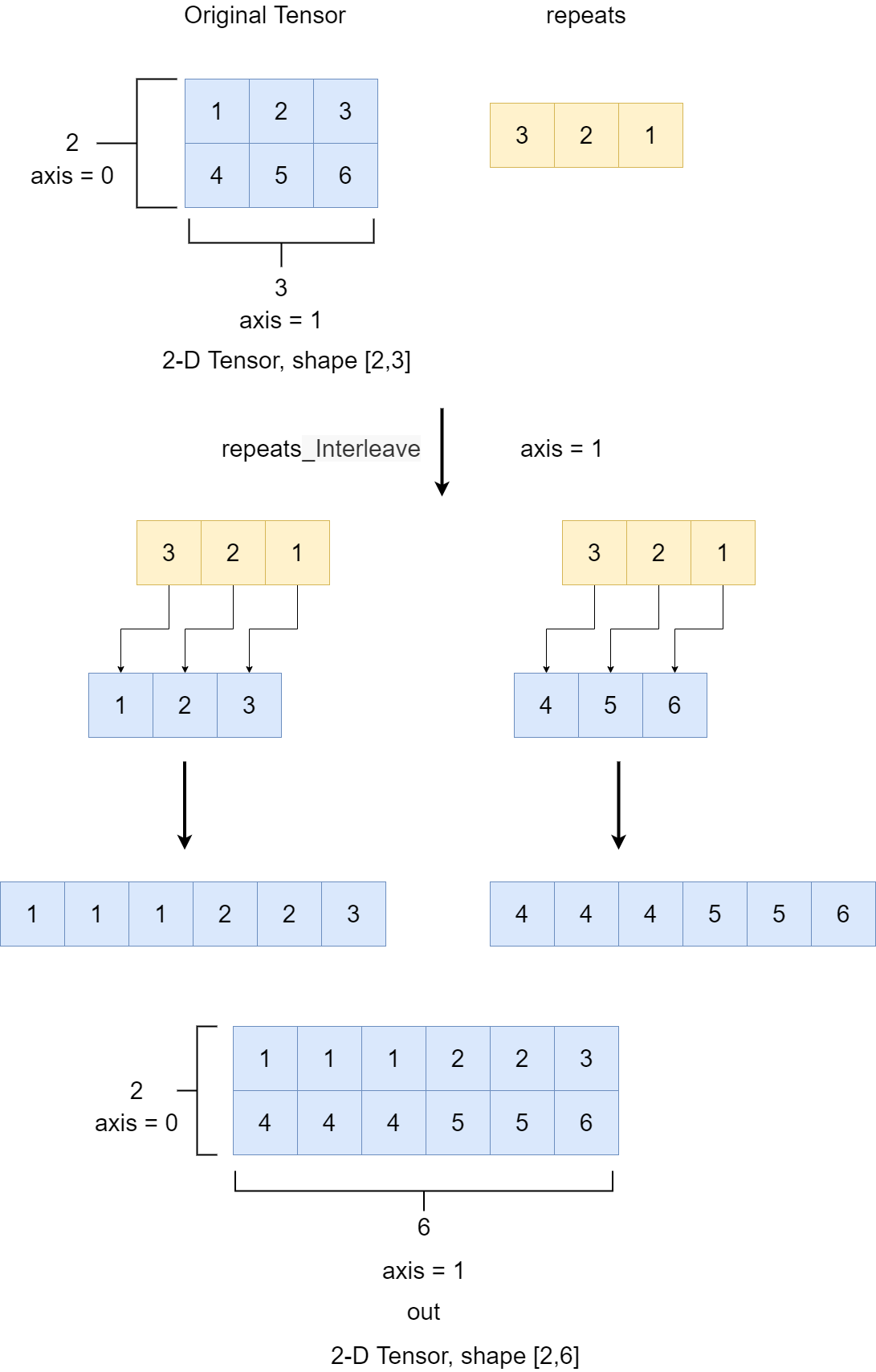

Parameters

x (Tensor) – The input Tensor to be operated. The data of x can be one of float32, float64, int32, int64.
repeats (Tensor|int) – The number of repetitions for each element. repeats is broadcasted to fit the shape of the given axis.
axis (int|None, optional) – The dimension in which we manipulate. Default: None, the output tensor is flatten.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, A Tensor with same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2, 3], [4, 5, 6]])
>>> repeats = paddle.to_tensor([3, 2, 1], dtype='int32')

>>> out = paddle.repeat_interleave(x, repeats, 1)
>>> print(out)
Tensor(shape=[2, 6], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 1, 1, 2, 2, 3],
 [4, 4, 4, 5, 5, 6]])

>>> out = paddle.repeat_interleave(x, 2, 0)
>>> print(out)
Tensor(shape=[4, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 2, 3],
 [1, 2, 3],
 [4, 5, 6],
 [4, 5, 6]])

>>> out = paddle.repeat_interleave(x, 2, None)
>>> print(out)
Tensor(shape=[12], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 1, 2, 2, 3, 3, 4, 4, 5, 5, 6, 6])

reshape ( shape: ShapeLike, name: str | None = None ) → Tensor [source] reshape¶

Changes the shape of x without changing its data.

Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode. If you want to use the Tensor copy version, please use Tensor.clone like reshape_clone_x = x.reshape([-1]).clone().

Some tricks exist when specifying the target shape.

-1 means the value of this dimension is inferred from the total element number of x and remaining dimensions. Thus one and only one dimension can be set -1.

0 means the actual dimension value is going to be copied from the corresponding dimension of x. The index of 0s in shape can not exceed the dimension of x.

Here are some examples to explain it.

Given a 3-D tensor x with a shape [2, 4, 6], and the target shape is [6, 8], the reshape operator will transform x into a 2-D tensor with shape [6, 8] and leaving x’s data unchanged.

Given a 3-D tensor x with a shape [2, 4, 6], and the target shape specified is [2, 3, -1, 2], the reshape operator will transform x into a 4-D tensor with shape [2, 3, 4, 2] and leaving x’s data unchanged. In this case, one dimension of the target shape is set to -1, the value of this dimension is inferred from the total element number of x and remaining dimensions.

Given a 3-D tensor x with a shape [2, 4, 6], and the target shape is [-1, 0, 3, 2], the reshape operator will transform x into a 4-D tensor with shape [2, 4, 3, 2] and leaving x’s data unchanged. In this case, besides -1, 0 means the actual dimension value is going to be copied from the corresponding dimension of x.

The following figure illustrates the first example – a 3D tensor of shape [2, 4, 6] is transformed into a 2D tensor of shape [6, 8], during which the order and values of the elements in the tensor remain unchanged. The elements in the two subdiagrams correspond to each other, clearly demonstrating how the reshape API works.

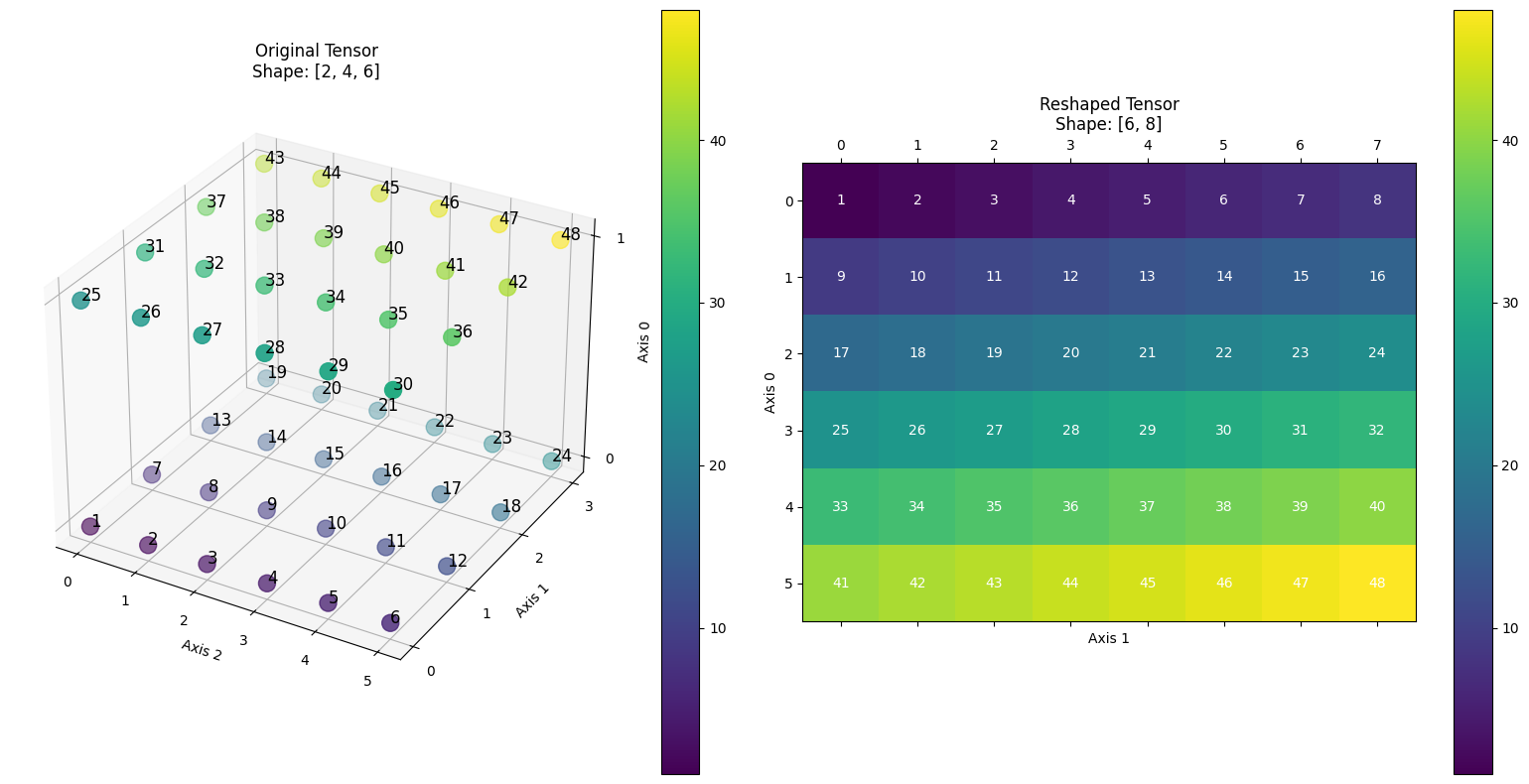
Parameters

x (Tensor) – An N-D Tensor. The data type is float16, float32, float64, int16, int32, int64, int8, uint8, complex64, complex128, bfloat16 or bool.
shape (list|tuple|Tensor) – Define the target shape. At most one dimension of the target shape can be -1. The data type is int32 . If shape is a list or tuple, each element of it should be integer or Tensor with shape []. If shape is a Tensor, it should be an 1-D Tensor .
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A reshaped Tensor with the same data type as x.

Examples

>>> import paddle

>>> x = paddle.rand([2, 4, 6], dtype="float32")
>>> positive_four = paddle.full([1], 4, "int32")

>>> out = paddle.reshape(x, [-1, 0, 3, 2])
>>> print(out.shape)
[2, 4, 3, 2]

>>> out = paddle.reshape(x, shape=[positive_four, 12])
>>> print(out.shape)
[4, 12]

>>> shape_tensor = paddle.to_tensor([8, 6], dtype=paddle.int32)
>>> out = paddle.reshape(x, shape=shape_tensor)
>>> print(out.shape)
[8, 6]
>>> # out shares data with x in dygraph mode
>>> x[0, 0, 0] = 10.
>>> print(out[0, 0])
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
10.)

reshape_ ( shape: ShapeLike, name: str | None = None ) → Tensor [source] reshape_¶: Inplace version of reshape API, the output Tensor will be inplaced with input x. Please refer to api_paddle_tensor_reshape.

resize_ ( shape: Sequence[int], fill_zero: bool = False, name: str | None = None ) → paddle.Tensor resize_¶

Resize x with specified shape.

Parameters

x (Tensor) – An arbitrary Tensor. The data type supports bfloat16, float16, float32, float64, bool, int8, int16, int32, int64, uint8, complex64 or complex128.
shape (list|tuple) – Define the target shape. Each element of it should be integer.
fill_zero (bool, optional) – If the size of specified shape is greater than the original Tensor size, the new Tensor will be filled with zero if fill_zero is True. Default: False, which means the filled value will be undetermined.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the resized Tensor.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1., 2., 3.])
>>> x.resize_([2, 1])
>>> print(x)
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.],
 [2.]])

>>> x = paddle.to_tensor([1., 2., 3.])
>>> x.resize_([2, 3], fill_zero=True)
>>> print(x)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 2., 3.],
 [0., 0., 0.]])

retain_grads ( ) retain_grads¶

Enables this Tensor to have their grad populated during backward(). It is a no-op for leaf tensors.

Returns: None.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1.0, 2.0, 3.0])
>>> x.stop_gradient = False
>>> y = x + x
>>> y.retain_grads()
>>> loss = y.sum()
>>> loss.backward()

>>> print(y.grad)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=False,
[1., 1., 1.])

>>> x = paddle.to_tensor([1.0, 2.0, 3.0])
>>> x.stop_gradient = False
>>> y = x + x
>>> y.retain_grads()
>>> loss = y.sum()
>>> loss.backward()

>>> print(y.grad)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=False,
[1., 1., 1.])

reverse ( axis: Sequence[int] | int, name: str | None = None ) → Tensor [source] reverse¶

Reverse the order of a n-D tensor along given axis in axis.

The image below illustrates how flip works.

Parameters

x (Tensor) – A Tensor with shape $[N_1, N_2,..., N_k]$ . The data type of the input Tensor x should be float32, float64, int32, int64, bool.
axis (list|tuple|int) – The axis(axes) to flip on. Negative indices for indexing from the end are accepted.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Tensor or DenseTensor calculated by flip layer. The data type is same with input x.

Examples

>>> 
>>> import paddle

>>> image_shape=(3, 2, 2)
>>> img = paddle.arange(image_shape[0] * image_shape[1] * image_shape[2]).reshape(image_shape)
>>> tmp = paddle.flip(img, [0,1])
>>> print(tmp)
Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[10, 11],
  [8 , 9 ]],
 [[6 , 7 ],
  [4 , 5 ]],
 [[2 , 3 ],
  [0 , 1 ]]])

>>> out = paddle.flip(tmp,-1)
>>> print(out)
Tensor(shape=[3, 2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[11, 10],
  [9 , 8 ]],
 [[7 , 6 ],
  [5 , 4 ]],
 [[3 , 2 ],
  [1 , 0 ]]])

roll ( shifts: int | Sequence[int], axis: int | Sequence[int] | None = None, name: str | None = None ) → Tensor [source] roll¶

Roll the x tensor along the given axis(axes). With specific ‘shifts’, Elements that roll beyond the last position are re-introduced at the first according to ‘shifts’. If a axis is not specified, the tensor will be flattened before rolling and then restored to the original shape.

Parameters

x (Tensor) – The x tensor as input.
shifts (int|list|tuple) – The number of places by which the elements of the x tensor are shifted.
axis (int|list|tuple, optional) – axis(axes) along which to roll. Default: None
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

The image below shows a 2D tensor [[1,2,3],[4,5,6],[7,8,9]] being transformed into tensors with different shapes through the roll operation.

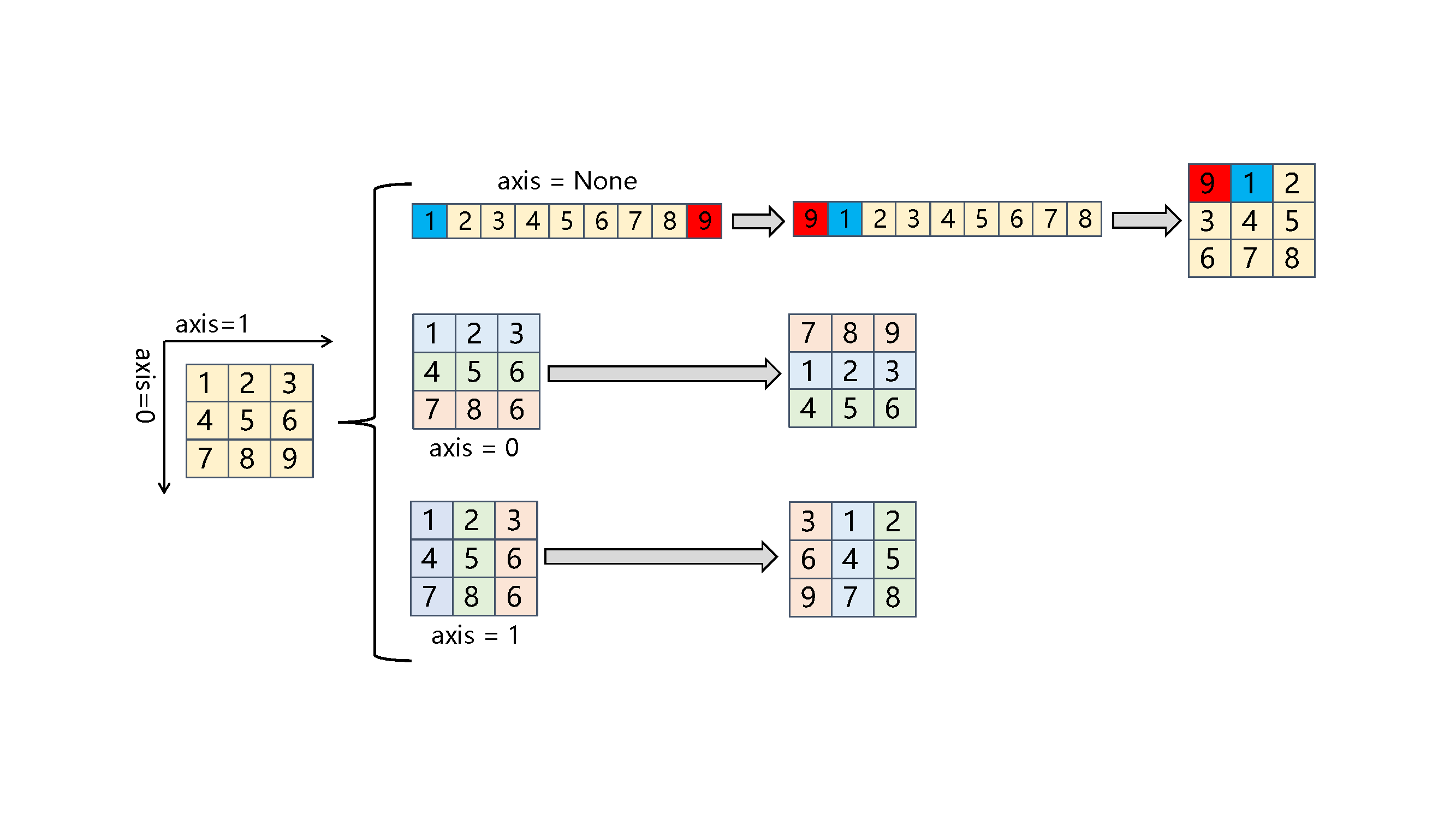
Returns: Tensor, A Tensor with same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0, 3.0],
...                       [4.0, 5.0, 6.0],
...                       [7.0, 8.0, 9.0]])
>>> out_z1 = paddle.roll(x, shifts=1)
>>> print(out_z1.numpy())
[[9. 1. 2.]
 [3. 4. 5.]
 [6. 7. 8.]]
>>> out_z2 = paddle.roll(x, shifts=1, axis=0)
>>> print(out_z2.numpy())
[[7. 8. 9.]
 [1. 2. 3.]
 [4. 5. 6.]]
>>> out_z3 = paddle.roll(x, shifts=1, axis=1)
>>> print(out_z3.numpy())
[[3. 1. 2.]
 [6. 4. 5.]
 [9. 7. 8.]]

rot90 ( k: int = 1, axes: Sequence[int] = [0, 1], name: str | None = None ) → Tensor [source] rot90¶

Rotate a n-D tensor by 90 degrees. The rotation direction and times are specified by axes and the absolute value of k. Rotation direction is from axes[0] towards axes[1] if k > 0, and from axes[1] towards axes[0] for k < 0.

Parameters

x (Tensor) – The input Tensor. The data type of the input Tensor x should be float16, float32, float64, int32, int64, bool. float16 is only supported on gpu.
k (int, optional) – Direction and number of times to rotate, default value: 1.
axes (list|tuple, optional) – Axes to rotate, dimension must be 2. default value: [0, 1].
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

Tensor, Tensor or DenseTensor calculated by rot90 layer. The data type is same with input x.

Examples

>>> import paddle

>>> data = paddle.arange(4)
>>> data = paddle.reshape(data, (2, 2))
>>> print(data.numpy())
[[0 1]
 [2 3]]

>>> y = paddle.rot90(data, 1, [0, 1])
>>> print(y.numpy())
[[1 3]
 [0 2]]

>>> y= paddle.rot90(data, -1, [0, 1])
>>> print(y.numpy())
[[2 0]
 [3 1]]

>>> data2 = paddle.arange(8)
>>> data2 = paddle.reshape(data2, (2,2,2))
>>> print(data2.numpy())
[[[0 1]
  [2 3]]
 [[4 5]
  [6 7]]]

>>> y = paddle.rot90(data2, 1, [1, 2])
>>> print(y.numpy())
[[[1 3]
  [0 2]]
 [[5 7]
  [4 6]]]

round ( decimals: int = 0, name: str | None = None ) → Tensor [source] round¶

Round the values in the input to the nearest integer value.

input:
  x.shape = [4]
  x.data = [1.2, -0.9, 3.4, 0.9]

output:
  out.shape = [4]
  out.data = [1., -1., 3., 1.]

Parameters

x (Tensor) – Input of Round operator, an N-D Tensor, with data type bfloat16, int32, int64, float32, float64, float16, complex64 or complex128.
decimals (int) – Rounded decimal place (default: 0).
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Round operator, a Tensor with shape same as input.

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.5, -0.2, 0.6, 1.5])
>>> out = paddle.round(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0., -0.,  1.,  2.])

round_ ( decimals=0, name=None ) round_¶: Inplace version of round API, the output Tensor will be inplaced with input x. Please refer to round.

rsqrt ( name: str | None = None ) → Tensor [source] rsqrt¶

Rsqrt Activation Operator.

Please make sure input is legal in case of numeric errors.

\[out = \frac{1}{\sqrt{x}}\]

Parameters

x (Tensor) – Input of Rsqrt operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Rsqrt operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([0.1, 0.2, 0.3, 0.4])
>>> out = paddle.rsqrt(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[3.16227770, 2.23606801, 1.82574177, 1.58113885])

rsqrt_ ( name=None ) rsqrt_¶: Inplace version of rsqrt API, the output Tensor will be inplaced with input x. Please refer to rsqrt.

scale ( scale: float | Tensor = 1.0, bias: float = 0.0, bias_after_scale: bool = True, act: str | None = None, name: str | None = None ) → Tensor [source] scale¶

Scale operator.

Putting scale and bias to the input Tensor as following:

bias_after_scale is True:

\[Out=scale*X+bias\]

bias_after_scale is False:

\[Out=scale*(X+bias)\]

Parameters

x (Tensor) – Input N-D Tensor of scale operator. Data type can be bfloat16, float16, float32, float64, int8, int16, int32, int64, uint8, complex64, complex128.
scale (float|Tensor) – The scale factor of the input, it should be a float number or a 0-D Tensor with shape [] and data type as float32.
bias (float) – The bias to be put on the input.
bias_after_scale (bool) – Apply bias addition after or before scaling. It is useful for numeric stability in some circumstances.
act (str|None, optional) – Activation applied to the output such as tanh, softmax, sigmoid, relu.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Output Tensor of scale operator, with shape and data type same as input.

Return type

Tensor

Examples

>>> # scale as a float32 number
>>> import paddle

>>> data = paddle.arange(6).astype("float32").reshape([2, 3])
>>> print(data)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 1., 2.],
 [3., 4., 5.]])
>>> res = paddle.scale(data, scale=2.0, bias=1.0)
>>> print(res)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1. , 3. , 5. ],
 [7. , 9. , 11.]])

>>> # scale with parameter scale as a Tensor
>>> import paddle

>>> data = paddle.arange(6).astype("float32").reshape([2, 3])
>>> print(data)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 1., 2.],
 [3., 4., 5.]])
>>> factor = paddle.to_tensor([2], dtype='float32')
>>> res = paddle.scale(data, scale=factor, bias=1.0)
>>> print(res)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1. , 3. , 5. ],
 [7. , 9. , 11.]])

scale_ ( scale: float = 1.0, bias: float = 0.0, bias_after_scale: bool = True, act: str | None = None, name: str | None = None ) → Tensor scale_¶: Inplace version of scale API, the output Tensor will be inplaced with input x. Please refer to scale.

scatter ( index: Tensor, updates: Tensor, overwrite: bool = True, name: str | None = None ) → Tensor [source] scatter¶

Scatter Layer Output is obtained by updating the input on selected indices based on updates.

As shown in the figure, when overwrite is set to True, the output for the same index is updated in overwrite mode, where x[index[i]] is directly replaced with update[i] sequentially; When overwrite is set to False, the output for the same index is updated in accumulation mode. In this mode, x[index[i]] is first initialized with elements set to 0. Then, update[i] is sequentially added to x[index[i]] to produce the output.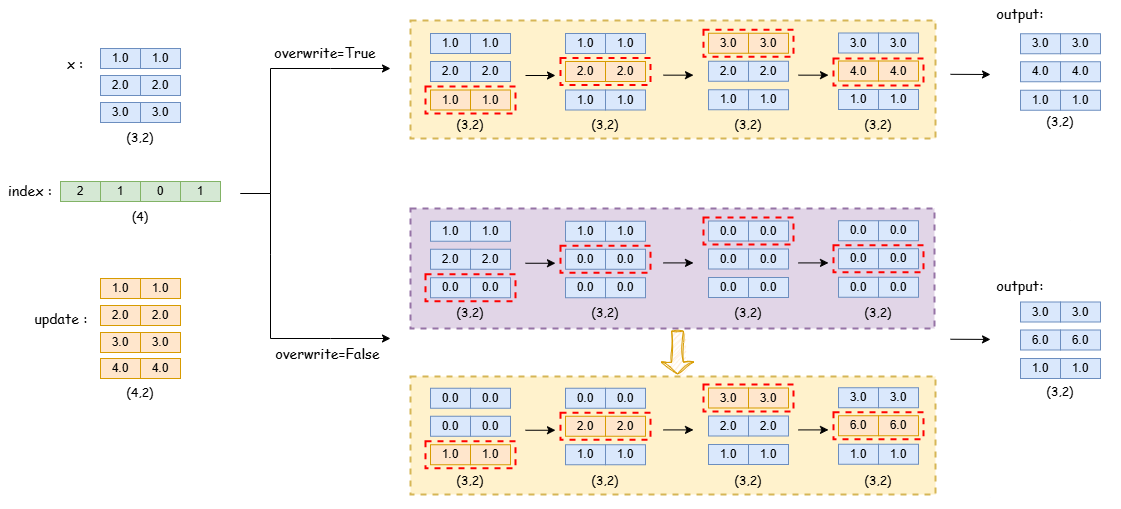

>>> import paddle
>>> #input:
>>> x = paddle.to_tensor([[1, 1], [2, 2], [3, 3]], dtype='float32')
>>> index = paddle.to_tensor([2, 1, 0, 1], dtype='int64')
>>> # shape of updates should be the same as x
>>> # shape of updates with dim > 1 should be the same as input
>>> updates = paddle.to_tensor([[1, 1], [2, 2], [3, 3], [4, 4]], dtype='float32')
>>> overwrite = False
>>> # calculation:
>>> if not overwrite:
...     for i in range(len(index)):
...         x[index[i]] = paddle.zeros([2])
>>> for i in range(len(index)):
...     if (overwrite):
...         x[index[i]] = updates[i]
...     else:
...         x[index[i]] += updates[i]
>>> # output:
>>> out = paddle.to_tensor([[3, 3], [6, 6], [1, 1]])
>>> print(out.shape)
[3, 2]

NOTICE: The order in which updates are applied is nondeterministic, so the output will be nondeterministic if index contains duplicates.

Parameters

x (Tensor) – The input N-D Tensor with ndim>=1. Data type can be float32, float64.
index (Tensor) – The index is a 1-D or 0-D Tensor. Data type can be int32, int64. The length of index cannot exceed updates’s length, and the value in index cannot exceed input’s length.
updates (Tensor) – Update input with updates parameter based on index. When the index is a 1-D tensor, the updates shape should be the same as input, and dim value with dim > 1 should be the same as input. When the index is a 0-D tensor, the updates should be a (N-1)-D tensor, the ith dim of the updates should be equal with the (i+1)th dim of the input.
overwrite (bool, optional) – The mode that updating the output when there are same indices.If True, use the overwrite mode to update the output of the same index,if False, use the accumulate mode to update the output of the same index. Default value is True.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

Tensor, The output is a Tensor with the same shape as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 1], [2, 2], [3, 3]], dtype='float32')
>>> index = paddle.to_tensor([2, 1, 0, 1], dtype='int64')
>>> updates = paddle.to_tensor([[1, 1], [2, 2], [3, 3], [4, 4]], dtype='float32')

>>> output1 = paddle.scatter(x, index, updates, overwrite=False)
>>> print(output1)
Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[3., 3.],
 [6., 6.],
 [1., 1.]])

>>> output2 = paddle.scatter(x, index, updates, overwrite=True)
>>> # CPU device:
>>> # [[3., 3.],
>>> #  [4., 4.],
>>> #  [1., 1.]]
>>> # GPU device maybe have two results because of the repeated numbers in index
>>> # result 1:
>>> # [[3., 3.],
>>> #  [4., 4.],
>>> #  [1., 1.]]
>>> # result 2:
>>> # [[3., 3.],
>>> #  [2., 2.],
>>> #  [1., 1.]]

scatter_ ( index: Tensor, updates: Tensor, overwrite: bool = True, name: str | None = None ) → Tensor [source] scatter_¶: Inplace version of scatter API, the output Tensor will be inplaced with input x. Please refer to api_paddle_tensor_scatter.

scatter_nd ( updates: Tensor, shape: ShapeLike, name: str | None = None ) → Tensor [source] scatter_nd¶

Scatter_nd Layer

Output is obtained by scattering the updates in a new tensor according to index . This op is similar to scatter_nd_add, except the tensor of shape is zero-initialized. Correspondingly, scatter_nd(index, updates, shape) is equal to scatter_nd_add(paddle.zeros(shape, updates.dtype), index, updates) . If index has repeated elements, then the corresponding updates are accumulated. Because of the numerical approximation issues, the different order of repeated elements in index may cause different results. The specific calculation method can be seen scatter_nd_add . This op is the inverse of the gather_nd op.

Parameters

index (Tensor) – The index input with ndim >= 1 and index.shape[-1] <= len(shape). Its dtype should be int32 or int64 as it is used as indexes.
updates (Tensor) – The updated value of scatter_nd op. Its dtype should be float32, float64. It must have the shape index.shape[:-1] + shape[index.shape[-1]:]
shape (tuple|list|Tensor) – Shape of output tensor.
name (str|None, optional) – The output Tensor name. If set None, the layer will be named automatically.

Returns

output (Tensor), The output is a tensor with the same type as updates .

Examples

>>> import paddle

>>> index = paddle.to_tensor([[1, 1],
...                           [0, 1],
...                           [1, 3]], dtype="int64")
>>> updates = paddle.rand(shape=[3, 9, 10], dtype='float32')
>>> shape = [3, 5, 9, 10]

>>> output = paddle.scatter_nd(index, updates, shape)

scatter_nd_add ( index: Tensor, updates: Tensor, name: str | None = None ) → Tensor [source] scatter_nd_add¶

Output is obtained by applying sparse addition to a single value or slice in a Tensor.

x is a Tensor with ndim $R$ and index is a Tensor with ndim $K$ . Thus, index has shape $[i_0, i_1, ..., i_{K-2}, Q]$ where $Q \leq R$ . updates is a Tensor with ndim $K - 1 + R - Q$ and its shape is $index.shape[:-1] + x.shape[index.shape[-1]:]$ .

According to the $[i_0, i_1, ..., i_{K-2}]$ of index , add the corresponding updates slice to the x slice which is obtained by the last one dimension of index .

Given:

* Case 1:
    x = [0, 1, 2, 3, 4, 5]
    index = [[1], [2], [3], [1]]
    updates = [9, 10, 11, 12]

  we get:

    output = [0, 22, 12, 14, 4, 5]

* Case 2:
    x = [[65, 17], [-14, -25]]
    index = [[], []]
    updates = [[[-1, -2], [1, 2]],
               [[3, 4], [-3, -4]]]
    x.shape = (2, 2)
    index.shape = (2, 0)
    updates.shape = (2, 2, 2)

  we get:

    output = [[67, 19], [-16, -27]]

Parameters

x (Tensor) – The x input. Its dtype should be int32, int64, float32, float64.
index (Tensor) – The index input with ndim > 1 and index.shape[-1] <= x.ndim. Its dtype should be int32 or int64 as it is used as indexes.
updates (Tensor) – The updated value of scatter_nd_add op, and it must have the same dtype as x. It must have the shape index.shape[:-1] + x.shape[index.shape[-1]:].
name (str|None, optional) – The output tensor name. If set None, the layer will be named automatically.

Returns

output (Tensor), The output is a tensor with the same shape and dtype as x.

Examples

>>> import paddle

>>> x = paddle.rand(shape=[3, 5, 9, 10], dtype='float32')
>>> updates = paddle.rand(shape=[3, 9, 10], dtype='float32')
>>> index = paddle.to_tensor([[1, 1],
...                           [0, 1],
...                           [1, 3]], dtype='int64')

>>> output = paddle.scatter_nd_add(x, index, updates)
>>> print(output.shape)
[3, 5, 9, 10]

select_scatter ( values: Tensor, axis: int, index: int, name: str | None = None ) → Tensor [source] select_scatter¶

Embeds the values of the values tensor into x at the given index of axis.

Parameters

x (Tensor) – The Destination Tensor. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
values (Tensor) – The tensor to embed into x. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
axis (int) – the dimension to insert the slice into.
index (int) – the index to select with.
name (str|None, optional) – Name for the operation (optional, default is None).

Returns

Tensor, same dtype and shape with x

Examples

>>> import paddle

>>> x = paddle.zeros((2,3,4)).astype("float32")
>>> values = paddle.ones((2,4)).astype("float32")
>>> res = paddle.select_scatter(x,values,1,1)
>>> print(res)
Tensor(shape=[2, 3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
       [[[0., 0., 0., 0.],
         [1., 1., 1., 1.],
         [0., 0., 0., 0.]],
        [[0., 0., 0., 0.],
         [1., 1., 1., 1.],
         [0., 0., 0., 0.]]])

set_ ( source: paddle.Tensor | None = None, shape: Sequence[int] | None = None, stride: Sequence[int] | None = None, offset: int = 0, name: str | None = None ) → paddle.Tensor set_¶

set x with specified source Tensor’s underlying storage, shape, stride and offset.

Note that the x will share the same data with source Tensor.

Parameters

x (Tensor) – An arbitrary Tensor. The data type supports bfloat16, float16, float32, float64, bool, int8, int16, int32, int64, uint8, complex64 or complex128.
source (Tensor|None, optional) – Define the target Tensor to use. The data type supports bfloat16, float16, float32, float64, bool, int8, int16, int32, int64, uint8, complex64 or complex128. Default: None, which means to set x with an empty source tensor.
shape (list|tuple|None, optional) – Define the target shape. Each element of it should be integer. Default: None, which means it will use the specified source’s shape as default value.
stride (list|tuple|None, optional) – Define the target stride. Each element of it should be integer. Default: None, and when shape is also None, it will use the specified source’s stride as default value; when shape is specified, it will use the default stride corresponding to the specified shape.
offset (int, optional) – Define the target offset from x’s holder. Default: 0.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, the Tensor with the same data type as x.

Examples

>>> import paddle

>>> src = paddle.to_tensor([[11., 22., 33.]])
>>> src2 = paddle.to_tensor([11., 22., 33., 44., 55., 66.])

>>> x = paddle.to_tensor([1., 2., 3., 4., 5.])
>>> x.set_()
>>> print(x)
Tensor(shape=[0], dtype=float32, place=Place(cpu), stop_gradient=True,
[])

>>> x = paddle.to_tensor([1., 2., 3., 4., 5.])
>>> x.set_(src)
>>> print(x)
Tensor(shape=[1, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[11., 22., 33.]])

>>> print(x._is_shared_buffer_with(src))
True

>>> x = paddle.to_tensor([1., 2., 3., 4., 5.])
>>> x.set_(src, shape=[2, 1])
>>> print(x)
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[11.],
 [22.]])

>>> x = paddle.to_tensor([1., 2., 3., 4., 5.])
>>> x.set_(src2, shape=[3], stride=[2])
>>> print(x)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[11., 33., 55.])

>>> x = paddle.to_tensor([1., 2., 3., 4., 5.])
>>> x.set_(src2, shape=[5], offset=4)
>>> print(x)
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[22., 33., 44., 55., 66.])

set_value ( value: Tensor | npt.NDArray[Any] | dict[str, int] | str ) → None set_value¶

Notes:: This API is ONLY available in Dygraph mode

Set a new value for this Variable.

Parameters: value (Variable|np.ndarray) – the new value.

Examples

>>> import paddle.base as base
>>> import paddle
>>> from paddle.nn import Linear
>>> import numpy as np

>>> data = np.ones([3, 1024], dtype='float32')
>>> with base.dygraph.guard():
...     linear = Linear(1024, 4)
...     t = paddle.to_tensor(data)
...     linear(t)  # call with default weight
...     custom_weight = np.random.randn(1024, 4).astype("float32")
...     linear.weight.set_value(custom_weight)  # change existing weight
...     out = linear(t)  # call with different weight

sgn ( name: str | None = None ) → Tensor [source] sgn¶

For complex tensor, this API returns a new tensor whose elements have the same angles as the corresponding elements of input and absolute values of one. For other float dtype tensor, this API returns sign of every element in x: 1 for positive, -1 for negative and 0 for zero, same as paddle.sign.

Parameters

x (Tensor) – The input tensor, which data type should be float16, float32, float64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

A sign Tensor for real input, or normalized Tensor for complex input, shape and data type are same as input.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([[3 + 4j, 7 - 24j, 0, 1 + 2j], [6 + 8j, 3, 0, -2]])
>>> paddle.sgn(x)
Tensor(shape=[2, 4], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[ (0.6000000238418579+0.800000011920929j),
  (0.2800000011920929-0.9599999785423279j),
   0j                                     ,
  (0.4472135901451111+0.8944271802902222j)],
 [ (0.6000000238418579+0.800000011920929j),
   (1+0j)                                 ,
   0j                                     ,
  (-1+0j)                                 ]])

shape [source]

Tensor’s shape.

Returns: shape.
Return type: List

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.0, stop_gradient=False)
>>> print(x.shape)
[]

shard_index ( index_num: int, nshards: int, shard_id: int, ignore_value: int = -1 ) → Tensor [source] shard_index¶

Reset the values of input according to the shard it belongs to. Every value in input must be a non-negative integer, and the parameter index_num represents the integer above the maximum value of input. Thus, all values in input must be in the range [0, index_num) and each value can be regarded as the offset to the beginning of the range. The range is further split into multiple shards. Specifically, we first compute the shard_size according to the following formula, which represents the number of integers each shard can hold. So for the i’th shard, it can hold values in the range [i*shard_size, (i+1)*shard_size).

shard_size = (index_num + nshards - 1) // nshards

For each value v in input, we reset it to a new value according to the following formula:

v = v - shard_id * shard_size if shard_id * shard_size <= v < (shard_id+1) * shard_size else ignore_value

That is, the value v is set to the new offset within the range represented by the shard shard_id if it in the range. Otherwise, we reset it to be ignore_value.

As shown below, a [2, 1] 2D tensor is updated with the shard_index operation. Given index_num = 20, nshards = 2, and shard_id = 0, the shard size is shard_size = (20 + 2 - 1) // 2 = 10. For each label element: if its value is in [0, 10), it’s adjusted to its offset; e.g., 1 becomes 1 - 0 * 10 = 1. Otherwise, it’s set to the default ignore_value of -1, like 16 becoming -1.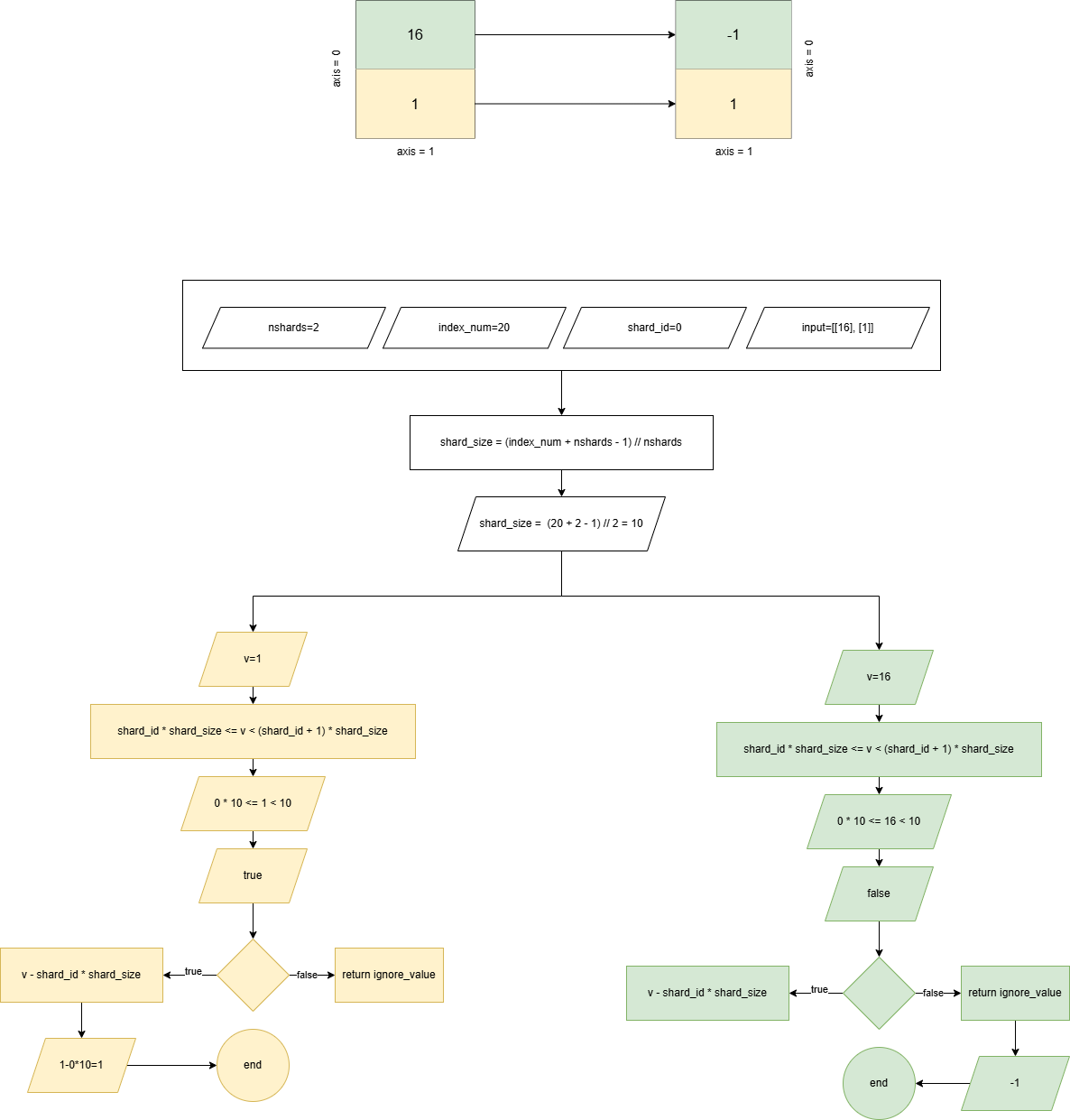

Parameters

input (Tensor) – Input tensor with data type int64 or int32. It’s last dimension must be 1.
index_num (int) – An integer represents the integer above the maximum value of input.
nshards (int) – The number of shards.
shard_id (int) – The index of the current shard.
ignore_value (int, optional) – An integer value out of sharded index range. The default value is -1.

Returns

Tensor.

Examples

>>> import paddle
>>> label = paddle.to_tensor([[16], [1]], "int64")
>>> shard_label = paddle.shard_index(input=label,
...                                  index_num=20,
...                                  nshards=2,
...                                  shard_id=0)
>>> print(shard_label.numpy())
[[-1]
 [ 1]]

sigmoid ( name: str | None = None ) → Tensor sigmoid¶

Sigmoid Activation.

\[out = \frac{1}{1 + e^{-x}}\]

Parameters

x (Tensor) – Input of Sigmoid operator, an N-D Tensor, with data type bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Sigmoid operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle
>>> import paddle.nn.functional as F

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = F.sigmoid(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.40131235, 0.45016602, 0.52497917, 0.57444251])

sigmoid_ ( name=None ) sigmoid_¶: Inplace version of sigmoid API, the output Tensor will be inplaced with input x. Please refer to api_paddle_sigmoid.

sign ( name: str | None = None ) → Tensor [source] sign¶

Returns sign of every element in x: For real numbers, 1 for positive, -1 for negative and 0 for zero. For complex numbers, the return value is a complex number with unit magnitude. If a complex number element is zero, the result is 0+0j.

Parameters

x (Tensor) – The input tensor. The data type can be uint8, int8, int16, int32, int64, bfloat16, float16, float32, float64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output sign tensor with identical shape and data type to the input x.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.to_tensor([3.0, 0.0, -2.0, 1.7], dtype='float32')
>>> out = paddle.sign(x=x)
>>> out
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[ 1.,  0., -1.,  1.])

signbit ( name: str | None = None ) → Tensor [source] signbit¶

Tests if each element of input has its sign bit set or not.

Parameters

x (Tensor) – The input Tensor. Must be one of the following types: float16, float32, float64, bfloat16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None).For more information, please refer to Name.

Returns

The output Tensor. The sign bit of the corresponding element of the input tensor, True means negative, False means positive.

Return type

out (Tensor)

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> x = paddle.to_tensor([-0., 1.1, -2.1, 0., 2.5], dtype='float32')
>>> res = paddle.signbit(x)
>>> print(res)
Tensor(shape=[5], dtype=bool, place=Place(cpu), stop_gradient=True,
[True, False, True, False, False])

>>> import paddle
>>> paddle.set_device('cpu')
>>> x = paddle.to_tensor([-5, -2, 3], dtype='int32')
>>> res = paddle.signbit(x)
>>> print(res)
Tensor(shape=[3], dtype=bool, place=Place(cpu), stop_gradient=True,
[True , True , False])

sin ( name: str | None = None ) → Tensor [source] sin¶

Sine Activation Operator.

\[out = sin(x)\]

Parameters

x (Tensor) – Input of Sin operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Sin operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.sin(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.38941833, -0.19866933,  0.09983342,  0.29552022])

sin_ ( name=None ) sin_¶: Inplace version of sin API, the output Tensor will be inplaced with input x. Please refer to sin.

sinc ( name: str | None = None ) → Tensor [source] sinc¶

Calculate the normalized sinc of x elementwise.

\[\begin{split}out_i = \left\{ \begin{aligned} &1 & \text{ if $x_i = 0$} \\ &\frac{\sin(\pi x_i)}{\pi x_i} & \text{ otherwise} \end{aligned} \right.\end{split}\]

Parameters

x (Tensor) – The input Tensor. Must be one of the following types: bfloat16, float16, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

out (Tensor), The Tensor of elementwise-computed normalized sinc result.

Examples

>>> import paddle
>>> paddle.set_device('cpu')
>>> paddle.seed(100)
>>> x = paddle.rand([2,3], dtype='float32')
>>> res = paddle.sinc(x)
>>> print(res)
Tensor(shape=[2, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.56691176, 0.93089867, 0.99977750],
 [0.61639023, 0.79618412, 0.89171958]])

sinc_ ( name: str | None = None ) → Tensor [source] sinc_¶: Inplace version of sinc API, the output Tensor will be inplaced with input x. Please refer to sinc.

sinh ( name: str | None = None ) → Tensor [source] sinh¶

Sinh Activation Operator.

\[out = sinh(x)\]

Parameters

x (Tensor) – Input of Sinh operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Sinh operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.sinh(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.41075233, -0.20133601,  0.10016675,  0.30452031])

sinh_ ( name=None ) sinh_¶: Inplace version of sinh API, the output Tensor will be inplaced with input x. Please refer to sinh.

This operator produces a slice of input along multiple axes. Similar to numpy: https://docs.scipy.org/doc/numpy/reference/arrays.indexing.html Slice uses axes, starts and ends attributes to specify the start and end dimension for each axis in the list of axes and Slice uses this information to slice the input data tensor. If a negative value is passed to starts or ends such as $-i$, it represents the reverse position of the axis $i-1$ (here 0 is the initial position). If the value passed to starts or ends is greater than n (the number of elements in this dimension), it represents n. For slicing to the end of a dimension with unknown size, it is recommended to pass in INT_MAX. The size of axes must be equal to starts and ends. Following examples will explain how slice works:

Case1:
    Given:
        data = [ [1, 2, 3, 4], [5, 6, 7, 8], ]
        axes = [0, 1]
        starts = [1, 0]
        ends = [2, 3]
    Then:
        result = [ [5, 6, 7], ]

Case2:
    Given:
        data = [ [1, 2, 3, 4], [5, 6, 7, 8], ]
        axes = [0, 1]
        starts = [0, 1]
        ends = [-1, 1000]       # -1 denotes the reverse 0th position of dimension 0.
    Then:
        result = [ [2, 3, 4], ] # result = data[0:1, 1:4]

The following figure illustrates the first case – a 2D tensor of shape [2, 4] is transformed into a 2D tensor of shape [1, 3] through a slicing operation.

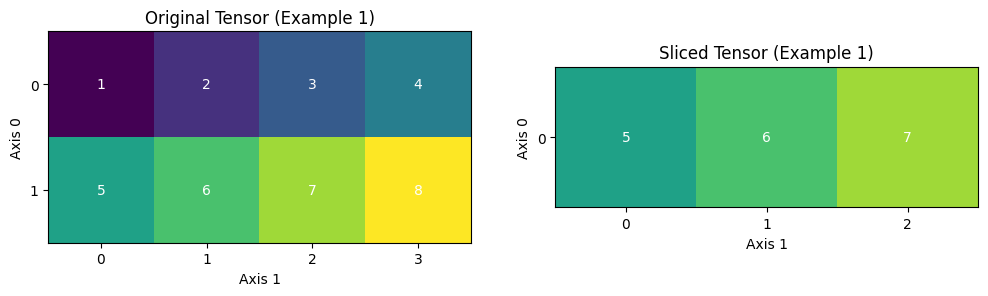
Parameters

input (Tensor) – A Tensor . The data type is float16, float32, float64, int32 or int64.
axes (list|tuple) – The data type is int32 . Axes that starts and ends apply to .
starts (list|tuple|Tensor) – The data type is int32 . If starts is a list or tuple, each element of it should be integer or 0-D int Tensor with shape []. If starts is an Tensor, it should be an 1-D Tensor. It represents starting indices of corresponding axis in axes.
ends (list|tuple|Tensor) – The data type is int32 . If ends is a list or tuple, each element of it should be integer or 0-D int Tensor with shape []. If ends is an Tensor, it should be an 1-D Tensor . It represents ending indices of corresponding axis in axes.

Returns

Tensor, A Tensor. The data type is same as input.

Examples

>>> import paddle

>>> input = paddle.rand(shape=[4, 5, 6], dtype='float32')
>>> # example 1:
>>> # attr starts is a list which doesn't contain tensor.
>>> axes = [0, 1, 2]
>>> starts = [-3, 0, 2]
>>> ends = [3, 2, 4]
>>> sliced_1 = paddle.slice(input, axes=axes, starts=starts, ends=ends)
>>> # sliced_1 is input[1:3, 0:2, 2:4].

>>> # example 2:
>>> # attr starts is a list which contain tensor.
>>> minus_3 = paddle.full([1], -3, "int32")
>>> sliced_2 = paddle.slice(input, axes=axes, starts=[minus_3, 0, 2], ends=ends)
>>> # sliced_2 is input[1:3, 0:2, 2:4].

slice_scatter ( value: Tensor, axes: Sequence[int], starts: Sequence[int], ends: Sequence[int], strides: Sequence[int], name: str | None = None ) → Tensor [source] slice_scatter¶

Embeds the value tensor into x along multiple axes. Returns a new tensor instead of a view. The size of axes must be equal to starts , ends and strides.

Parameters

x (Tensor) – The input Tensor. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
value (Tensor) – The tensor to embed into x. Supported data types are bool, float16, float32, float64, uint8, int8, int16, int32, int64, bfloat16, complex64, complex128.
axes (list|tuple) – the dimensions to insert the value.
starts (list|tuple) – the start indices of where to insert.
ends (list|tuple) – the stop indices of where to insert.
strides (list|tuple) – the steps for each insert.
name (str|None, optional) – Name for the operation (optional, default is None).

Returns

Tensor, same dtype and shape with x

Examples

>>> import paddle

>>> x = paddle.zeros((3, 9))
>>> value = paddle.ones((3, 2))
>>> res = paddle.slice_scatter(x, value, axes=[1], starts=[2], ends=[6], strides=[2])
>>> print(res)
Tensor(shape=[3, 9], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 0., 1., 0., 1., 0., 0., 0., 0.],
 [0., 0., 1., 0., 1., 0., 0., 0., 0.],
 [0., 0., 1., 0., 1., 0., 0., 0., 0.]])

>>> # broadcast `value` got the same result
>>> x = paddle.zeros((3, 9))
>>> value = paddle.ones((3, 1))
>>> res = paddle.slice_scatter(x, value, axes=[1], starts=[2], ends=[6], strides=[2])
>>> print(res)
Tensor(shape=[3, 9], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 0., 1., 0., 1., 0., 0., 0., 0.],
 [0., 0., 1., 0., 1., 0., 0., 0., 0.],
 [0., 0., 1., 0., 1., 0., 0., 0., 0.]])

>>> # broadcast `value` along multiple axes
>>> x = paddle.zeros((3, 3, 5))
>>> value = paddle.ones((1, 3, 1))
>>> res = paddle.slice_scatter(x, value, axes=[0, 2], starts=[1, 0], ends=[3, 4], strides=[1, 2])
>>> print(res)
Tensor(shape=[3, 3, 5], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[0., 0., 0., 0., 0.],
  [0., 0., 0., 0., 0.],
  [0., 0., 0., 0., 0.]],
 [[1., 0., 1., 0., 0.],
  [1., 0., 1., 0., 0.],
  [1., 0., 1., 0., 0.]],
 [[1., 0., 1., 0., 0.],
  [1., 0., 1., 0., 0.],
  [1., 0., 1., 0., 0.]]])

solve ( y: Tensor, left: bool = True, name: str | None = None ) → Tensor solve¶

Computes the solution of a square system of linear equations with a unique solution for input ‘X’ and ‘Y’. Let $X$ be a square matrix or a batch of square matrices, $Y$ be a vector/matrix or a batch of vectors/matrices. When left is True, the equation should be:

\[Out = X^-1 * Y\]

When left is False, the equation should be:

\[Out = Y * X^-1\]

Specifically, this system of linear equations has one solution if and only if input ‘X’ is invertible.

Parameters

x (Tensor) – A square matrix or a batch of square matrices. Its shape should be [*, M, M], where * is zero or more batch dimensions. Its data type should be float32 or float64.
y (Tensor) – A vector/matrix or a batch of vectors/matrices. Its shape should be [*, M, K], where * is zero or more batch dimensions. Its data type should be float32 or float64.
left (bool, optional) – Whether to solve the system $X * Out = Y$ or $Out * X = Y$. Default: True.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The solution of a square system of linear equations with a unique solution for input ‘x’ and ‘y’. Its data type should be the same as that of x.

Return type

Tensor

Examples

>>> # a square system of linear equations:
>>> # 3*X0 + X1 = 9
>>> # X0 + 2*X1 = 8

>>> import paddle

>>> x = paddle.to_tensor([[3, 1],[1, 2]], dtype="float64")
>>> y = paddle.to_tensor([9, 8], dtype="float64")
>>> out = paddle.linalg.solve(x, y)

>>> print(out)
Tensor(shape=[2], dtype=float64, place=Place(cpu), stop_gradient=True,
[2., 3.])

sort ( axis: int = -1, descending: bool = False, stable: bool = False, name: str | None = None ) → Tensor [source] sort¶

Sorts the input along the given axis, and returns the sorted output tensor. The default sort algorithm is ascending, if you want the sort algorithm to be descending, you must set the descending as True.

Parameters

x (Tensor) – An input N-D Tensor with type float32, float64, int16, int32, int64, uint8.
axis (int, optional) – Axis to compute indices along. The effective range is [-R, R), where R is Rank(x). when axis<0, it works the same way as axis+R. Default is -1.
descending (bool, optional) – Descending is a flag, if set to true, algorithm will sort by descending order, else sort by ascending order. Default is false.
stable (bool, optional) – Whether to use stable sorting algorithm or not. When using stable sorting algorithm, the order of equivalent elements will be preserved. Default is False.
name (str, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, sorted tensor(with the same shape and data type as x).

Examples

>>> import paddle

>>> x = paddle.to_tensor([[[5,8,9,5],
...                        [0,0,1,7],
...                        [6,9,2,4]],
...                       [[5,2,4,2],
...                        [4,7,7,9],
...                        [1,7,0,6]]],
...                      dtype='float32')
>>> out1 = paddle.sort(x=x, axis=-1)
>>> out2 = paddle.sort(x=x, axis=0)
>>> out3 = paddle.sort(x=x, axis=1)
>>> print(out1.numpy())
[[[5. 5. 8. 9.]
  [0. 0. 1. 7.]
  [2. 4. 6. 9.]]
 [[2. 2. 4. 5.]
  [4. 7. 7. 9.]
  [0. 1. 6. 7.]]]
>>> print(out2.numpy())
[[[5. 2. 4. 2.]
  [0. 0. 1. 7.]
  [1. 7. 0. 4.]]
 [[5. 8. 9. 5.]
  [4. 7. 7. 9.]
  [6. 9. 2. 6.]]]
>>> print(out3.numpy())
[[[0. 0. 1. 4.]
  [5. 8. 2. 5.]
  [6. 9. 9. 7.]]
 [[1. 2. 0. 2.]
  [4. 7. 4. 6.]
  [5. 7. 7. 9.]]]

sparse_dim ( ) sparse_dim¶

Returns the number of sparse dimensions of sparse Tensor.

Note

If self is not sparse Tensor, return 0.

Returns: int, sparse dim of self Tensor

Examples

>>> import paddle

>>> indices = [[0, 1, 2], [1, 2, 0]]
>>> values = [1.0, 2.0, 3.0]
>>> dense_shape = [3, 3]
>>> coo = paddle.sparse.sparse_coo_tensor(indices, values, dense_shape)
>>> coo.sparse_dim()
2

>>> crows = [0, 2, 3, 5]
>>> cols = [1, 3, 2, 0, 1]
>>> values = [1, 2, 3, 4, 5]
>>> dense_shape = [3, 4]
>>> csr = paddle.sparse.sparse_csr_tensor(crows, cols, values, dense_shape)
>>> csr.sparse_dim()
2

>>> dense = paddle.to_tensor([1, 2, 3])
>>> dense.sparse_dim()
0

split ( num_or_sections: int | Sequence[int], axis: int | Tensor = 0, name: str | None = None ) → list[Tensor] [source] split¶

Split the input tensor into multiple sub-Tensors.

Parameters

x (Tensor) – A N-D Tensor. The data type is bool, bfloat16, float16, float32, float64, uint8, int8, int32 or int64.
num_or_sections (int|list|tuple) – If num_or_sections is an int, then num_or_sections indicates the number of equal sized sub-Tensors that the x will be divided into. If num_or_sections is a list or tuple, the length of it indicates the number of sub-Tensors and the elements in it indicate the sizes of sub-Tensors’ dimension orderly. The length of the list must not be larger than the x ‘s size of specified axis.
axis (int|Tensor, optional) – The axis along which to split, it can be a integer or a 0-D Tensor with shape [] and data type int32 or int64. If :math::axis < 0, the axis to split along is $rank(x) + axis$. Default is 0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

list(Tensor), The list of segmented Tensors.

Examples

>>> import paddle

>>> # x is a Tensor of shape [3, 9, 5]
>>> x = paddle.rand([3, 9, 5])

>>> out0, out1, out2 = paddle.split(x, num_or_sections=3, axis=1)
>>> print(out0.shape)
[3, 3, 5]
>>> print(out1.shape)
[3, 3, 5]
>>> print(out2.shape)
[3, 3, 5]

>>> out0, out1, out2 = paddle.split(x, num_or_sections=[2, 3, 4], axis=1)
>>> print(out0.shape)
[3, 2, 5]
>>> print(out1.shape)
[3, 3, 5]
>>> print(out2.shape)
[3, 4, 5]

>>> out0, out1, out2 = paddle.split(x, num_or_sections=[2, 3, -1], axis=1)
>>> print(out0.shape)
[3, 2, 5]
>>> print(out1.shape)
[3, 3, 5]
>>> print(out2.shape)
[3, 4, 5]

>>> # axis is negative, the real axis is (rank(x) + axis)=1
>>> out0, out1, out2 = paddle.split(x, num_or_sections=3, axis=-2)
>>> print(out0.shape)
[3, 3, 5]
>>> print(out1.shape)
[3, 3, 5]
>>> print(out2.shape)
[3, 3, 5]

sqrt ( name: str | None = None ) → Tensor [source] sqrt¶

Sqrt Activation Operator.

\[out=\sqrt{x}=x^{1/2}\]

Parameters

x (Tensor) – Input of Sqrt operator, an N-D Tensor, with data type float32, float64, float16, bfloat16 uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Sqrt operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([0.1, 0.2, 0.3, 0.4])
>>> out = paddle.sqrt(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.31622776, 0.44721359, 0.54772258, 0.63245553])

sqrt_ ( name=None ) sqrt_¶: Inplace version of sqrt API, the output Tensor will be inplaced with input x. Please refer to sqrt.

square ( name: str | None = None ) → Tensor [source] square¶

Square each elements of the inputs.

\[out = x^2\]

Parameters

x (Tensor) – Input of Square operator, an N-D Tensor, with data type int32, int64, float32, float64, float16, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Square operator, a Tensor with shape same as input.

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.square(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.16000001, 0.04000000, 0.01000000, 0.09000000])

square_ ( name=None ) square_¶: Inplace version of square API, the output Tensor will be inplaced with input x. Please refer to square.

squeeze ( axis: int | Sequence[int] | None = None, name: str | None = None ) → Tensor [source] squeeze¶

Squeeze the dimension(s) of size 1 of input tensor x’s shape.

Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode. If you want to use the Tensor copy version, please use Tensor.clone like squeeze_clone_x = x.squeeze().clone().

If axis is provided, it will remove the dimension(s) by given axis that of size 1. If the dimension of given axis is not of size 1, the dimension remain unchanged. If axis is not provided, all dims equal of size 1 will be removed.

Case1:

  Input:
    x.shape = [1, 3, 1, 5]  # If axis is not provided, all dims equal of size 1 will be removed.
    axis = None
  Output:
    out.shape = [3, 5]

Case2:

  Input:
    x.shape = [1, 3, 1, 5]  # If axis is provided, it will remove the dimension(s) by given axis that of size 1.
    axis = 0
  Output:
    out.shape = [3, 1, 5]

Case4:

  Input:
    x.shape = [1, 3, 1, 5]  # If the dimension of one given axis (3) is not of size 1, the dimension remain unchanged.
    axis = [0, 2, 3]
  Output:
    out.shape = [3, 5]

Case4:

  Input:
    x.shape = [1, 3, 1, 5]  # If axis is negative, axis = axis + ndim (number of dimensions in x).
    axis = [-2]
  Output:
    out.shape = [1, 3, 5]

Parameters

x (Tensor) – The input Tensor. Supported data type: float32, float64, bool, int8, int32, int64.
axis (int|list|tuple, optional) – An integer or list/tuple of integers, indicating the dimensions to be squeezed. Default is None. The range of axis is $[-ndim(x), ndim(x))$. If axis is negative, $axis = axis + ndim(x)$. If axis is None, all the dimensions of x of size 1 will be removed.
name (str|None, optional) – Please refer to Name, Default None.

Returns

Tensor, Squeezed Tensor with the same data type as input Tensor.

Examples

>>> import paddle

>>> x = paddle.rand([5, 1, 10])
>>> output = paddle.squeeze(x, axis=1)

>>> print(x.shape)
[5, 1, 10]
>>> print(output.shape)
[5, 10]

>>> # output shares data with x in dygraph mode
>>> x[0, 0, 0] = 10.
>>> print(output[0, 0])
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
10.)

squeeze_ ( axis: int | Sequence[int] | None = None, name: str | None = None ) → Tensor [source] squeeze_¶: Inplace version of squeeze API, the output Tensor will be inplaced with input x. Please refer to api_paddle_tensor_squeeze.

stack ( axis: int = 0, name: str | None = None ) → Tensor [source] stack¶

Stacks all the input tensors x along axis dimension. All tensors must be of the same shape and same dtype.

For example, given N tensors of shape [A, B], if axis == 0, the shape of stacked tensor is [N, A, B]; if axis == 1, the shape of stacked tensor is [A, N, B], etc.

It also supports the operation with zero-size tensors which contain 0 in their shape. See the examples below.

Case 1:

  Input:
    x[0].shape = [1, 2]
    x[0].data = [ [1.0 , 2.0 ] ]
    x[1].shape = [1, 2]
    x[1].data = [ [3.0 , 4.0 ] ]
    x[2].shape = [1, 2]
    x[2].data = [ [5.0 , 6.0 ] ]

  Attrs:
    axis = 0

  Output:
    Out.dims = [3, 1, 2]
    Out.data =[ [ [1.0, 2.0] ],
                [ [3.0, 4.0] ],
                [ [5.0, 6.0] ] ]


Case 2:

  Input:
    x[0].shape = [1, 2]
    x[0].data = [ [1.0 , 2.0 ] ]
    x[1].shape = [1, 2]
    x[1].data = [ [3.0 , 4.0 ] ]
    x[2].shape = [1, 2]
    x[2].data = [ [5.0 , 6.0 ] ]


  Attrs:
    axis = 1 or axis = -2  # If axis = -2, axis = axis+ndim(x[0])+1 = -2+2+1 = 1.

  Output:
    Out.shape = [1, 3, 2]
    Out.data =[ [ [1.0, 2.0]
                  [3.0, 4.0]
                  [5.0, 6.0] ] ]


Case 3:

    Input:
        x[0].shape = [0, 1, 2]
        x[0].data = []
        x[1].shape = [0, 1, 2]
        x[1].data = []

    Attrs:
        axis = 0

    Output:
        Out.shape = [2, 0, 1, 2]
        Out.data = []


Case 4:

    Input:
        x[0].shape = [0, 1, 2]
        x[0].data = []
        x[1].shape = [0, 1, 2]
        x[1].data = []

    Attrs:
        axis = 1

    Output:
        Out.shape = [0, 2, 1, 2]
        Out.data = []

The image below demonstrates the Case 1: three 2-dimensional tensors with shape [1, 2] are stacked in the dimension of axis=0 to form a 3-dimensional tensor with shape [3, 1, 2] .

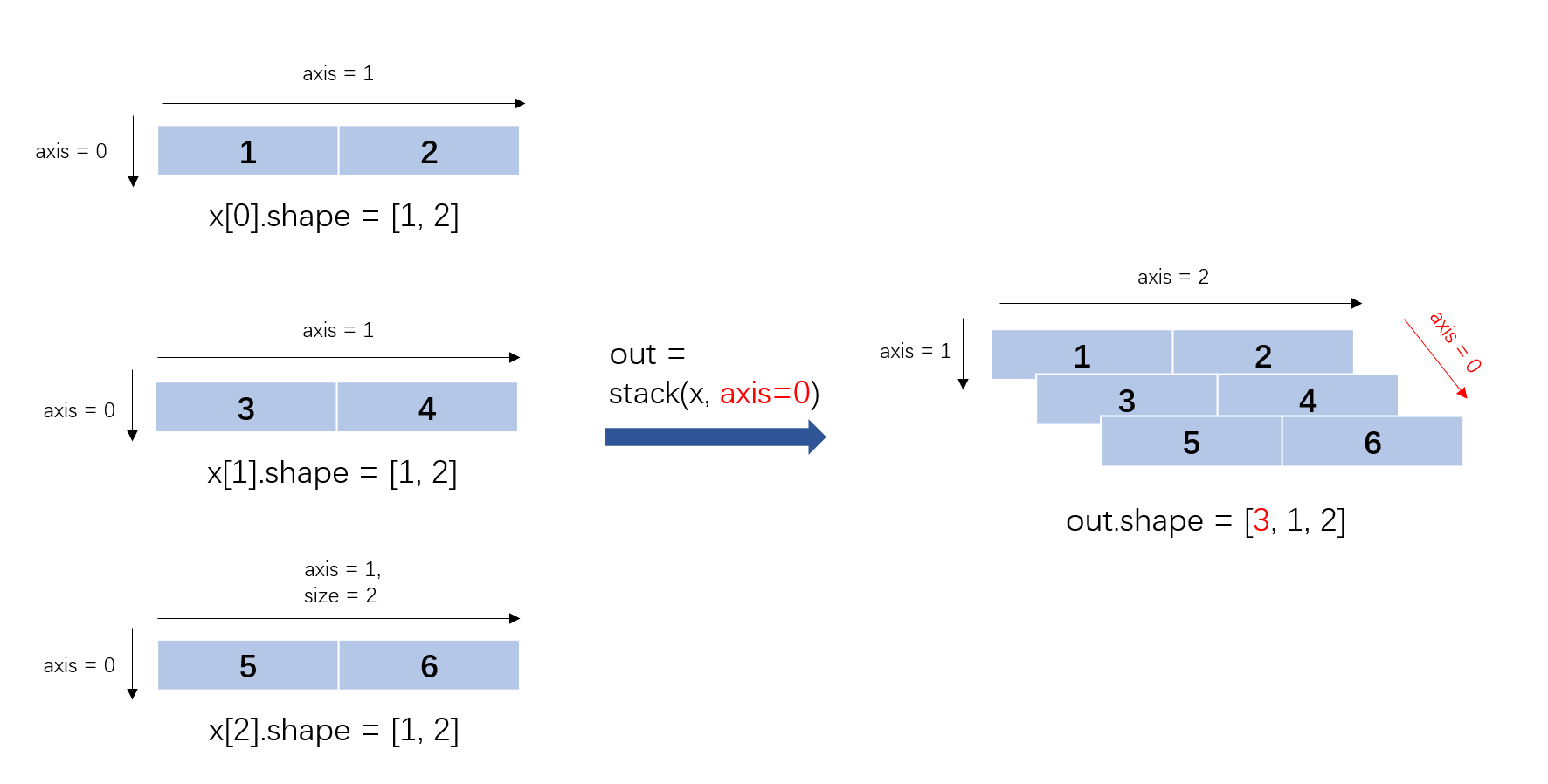
Parameters

x (list[Tensor]|tuple[Tensor]) – Input x can be a list or tuple of tensors, the Tensors in x must be of the same shape and dtype. Supported data types: float32, float64, int32, int64.
axis (int, optional) – The axis along which all inputs are stacked. axis range is [-(R+1), R+1), where R is the number of dimensions of the first input tensor x[0]. If axis < 0, axis = axis+R+1. The default value of axis is 0.
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, The stacked tensor with same data type as input.

Examples

>>> import paddle

>>> x1 = paddle.to_tensor([[1.0, 2.0]])
>>> x2 = paddle.to_tensor([[3.0, 4.0]])
>>> x3 = paddle.to_tensor([[5.0, 6.0]])

>>> out = paddle.stack([x1, x2, x3], axis=0)
>>> print(out.shape)
[3, 1, 2]
>>> print(out)
Tensor(shape=[3, 1, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[1., 2.]],
 [[3., 4.]],
 [[5., 6.]]])

>>> out = paddle.stack([x1, x2, x3], axis=-2)
>>> print(out.shape)
[1, 3, 2]
>>> print(out)
Tensor(shape=[1, 3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[[1., 2.],
  [3., 4.],
  [5., 6.]]])

>>> # zero-size tensors
>>> x1 = paddle.ones([0, 1, 2])
>>> x2 = paddle.ones([0, 1, 2])

>>> out = paddle.stack([x1, x2], axis=0)
>>> print(out.shape)
[2, 0, 1, 2]
>>> print(out)
Tensor(shape=[2, 0, 1, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[],
 []])

>>> out = paddle.stack([x1, x2], axis=1)
>>> print(out.shape)
[0, 2, 1, 2]
>>> print(out)
Tensor(shape=[0, 2, 1, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[])

stanh ( scale_a: float = 0.67, scale_b: float = 1.7159, name: str | None = None ) → Tensor [source] stanh¶

stanh activation.

\[out = b * \frac{e^{a * x} - e^{-a * x}}{e^{a * x} + e^{-a * x}}\]

Parameters

x (Tensor) – The input Tensor with data type bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64.
scale_a (float, optional) – The scale factor a of the input. Default is 0.67.
scale_b (float, optional) – The scale factor b of the output. Default is 1.7159.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

A Tensor with the same shape and data type as x (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([1.0, 2.0, 3.0, 4.0])
>>> out = paddle.stanh(x, scale_a=0.67, scale_b=1.72)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.00616539, 1.49927628, 1.65933096, 1.70390463])

std ( axis: int | Sequence[int] | None = None, unbiased: bool = True, keepdim: bool = False, name: str | None = None ) → Tensor [source] std¶

Computes the standard-deviation of x along axis .

Parameters

x (Tensor) – The input Tensor with data type float16, float32, float64.
axis (int|list|tuple|None, optional) – The axis along which to perform standard-deviation calculations. axis should be int, list(int) or tuple(int). If axis is a list/tuple of dimension(s), standard-deviation is calculated along all element(s) of axis . axis or element(s) of axis should be in range [-D, D), where D is the dimensions of x . If axis or element(s) of axis is less than 0, it works the same way as $axis + D$ . If axis is None, standard-deviation is calculated over all elements of x. Default is None.
unbiased (bool, optional) – Whether to use the unbiased estimation. If unbiased is True, the standard-deviation is calculated via the unbiased estimator. If unbiased is True, the divisor used in the computation is $N - 1$, where $N$ represents the number of elements along axis , otherwise the divisor is $N$. Default is True.
keepdim (bool, optional) – Whether to reserve the reduced dimension(s) in the output Tensor. If keepdim is True, the dimensions of the output Tensor is the same as x except in the reduced dimensions(it is of size 1 in this case). Otherwise, the shape of the output Tensor is squeezed in axis . Default is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of standard-deviation along axis of x, with the same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0, 3.0], [1.0, 4.0, 5.0]])
>>> out1 = paddle.std(x)
>>> print(out1.numpy())
1.6329932
>>> out2 = paddle.std(x, unbiased=False)
>>> print(out2.numpy())
1.490712
>>> out3 = paddle.std(x, axis=1)
>>> print(out3.numpy())
[1.       2.081666]

stft ( n_fft: int, hop_length: int | None = None, win_length: int | None = None, window: Tensor | None = None, center: bool = True, pad_mode: Literal['reflect', 'constant'] = 'reflect', normalized: bool = False, onesided: bool | None = None, name: str | None = None ) → Tensor stft¶

Short-time Fourier transform (STFT).

The STFT computes the discrete Fourier transforms (DFT) of short overlapping windows of the input using this formula:

\[X_t[f] = \sum_{n = 0}^{N-1} \text{window}[n]\ x[t \times H + n]\ e^{-{2 \pi j f n}/{N}}\]

Where: - $t$: The $t$-th input window. - $f$: Frequency $0 \leq f < \text{n_fft}$ for onesided=False, or $0 \leq f < \lfloor \text{n_fft} / 2 \rfloor + 1$ for onesided=True. - $N$: Value of n_fft. - $H$: Value of hop_length.

Parameters

x (Tensor) – The input data which is a 1-dimensional or 2-dimensional Tensor with shape […, seq_length]. It can be a real-valued or a complex Tensor.
n_fft (int) – The number of input samples to perform Fourier transform.
hop_length (int|None, optional) – Number of steps to advance between adjacent windows and 0 < hop_length. Default: None (treated as equal to n_fft//4)
win_length (int|None, optional) – The size of window. Default: None (treated as equal to n_fft)
window (Tensor|None, optional) – A 1-dimensional tensor of size win_length. It will be center padded to length n_fft if win_length < n_fft. Default: None ( treated as a rectangle window with value equal to 1 of size win_length).
center (bool, optional) – Whether to pad x to make that the $t \times hop\_length$ at the center of $t$-th frame. Default: True.
pad_mode (str, optional) – Choose padding pattern when center is True. See paddle.nn.functional.pad for all padding options. Default: “reflect”
normalized (bool, optional) – Control whether to scale the output by 1/sqrt(n_fft). Default: False
onesided (bool, optional) – Control whether to return half of the Fourier transform output that satisfies the conjugate symmetry condition when input is a real-valued tensor. It can not be True if input is a complex tensor. Default: None
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

The complex STFT output tensor with shape […, n_fft//2 + 1, num_frames] (real-valued input and onesided is True) or […, n_fft, num_frames] (onesided is False)

Examples

>>> import paddle
>>> from paddle.signal import stft

>>> # real-valued input
>>> x = paddle.randn([8, 48000], dtype=paddle.float64)
>>> y1 = stft(x, n_fft=512)
>>> print(y1.shape)
[8, 257, 376]

>>> y2 = stft(x, n_fft=512, onesided=False)
>>> print(y2.shape)
[8, 512, 376]

>>> # complex input
>>> x = paddle.randn([8, 48000], dtype=paddle.float64) + \
...         paddle.randn([8, 48000], dtype=paddle.float64)*1j
>>> print(x.shape)
[8, 48000]
>>> print(x.dtype)
paddle.complex128

>>> y1 = stft(x, n_fft=512, center=False, onesided=False)
>>> print(y1.shape)
[8, 512, 372]

stop_gradient

Tensor’s stop_gradient.

Returns: Tensor’s stop_gradient.
Return type: bool

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.)
>>> print(x.stop_gradient)
True

>>> x.stop_gradient = False
>>> print(x.stop_gradient)
False

This operator produces a slice of x along multiple axes. Similar to numpy: https://docs.scipy.org/doc/numpy/reference/arrays.indexing.html Slice uses axes, starts and ends attributes to specify the start and end dimension for each axis in the list of axes and Slice uses this information to slice the input data tensor. If a negative value is passed to starts or ends such as $-i$, it represents the reverse position of the axis $i-1$ th(here 0 is the initial position). The strides represents steps of slicing and if the strides is negative, slice operation is in the opposite direction. If the value passed to starts or ends is greater than n (the number of elements in this dimension), it represents n. For slicing to the end of a dimension with unknown size, it is recommended to pass in INT_MAX. The size of axes must be equal to starts , ends and strides. Following examples will explain how strided_slice works:

Case1:
    Given:
        data = [ [1, 2, 3, 4], [5, 6, 7, 8], ]
        axes = [0, 1]
        starts = [1, 0]
        ends = [2, 3]
        strides = [1, 1]
    Then:
        result = [ [5, 6, 7], ]

Case2:
    Given:
        data = [ [1, 2, 3, 4], [5, 6, 7, 8], ]
        axes = [0, 1]
        starts = [0, 1]
        ends = [2, 0]
        strides = [1, -1]
    Then:
        result = [ [8, 7, 6], ]
Case3:
    Given:
        data = [ [1, 2, 3, 4], [5, 6, 7, 8], ]
        axes = [0, 1]
        starts = [0, 1]
        ends = [-1, 1000]
        strides = [1, 3]
    Then:
        result = [ [2], ]

Parameters

x (Tensor) – An N-D Tensor. The data type is bool, float16, float32, float64, int32 or int64.
axes (list|tuple) – The data type is int32 . Axes that starts and ends apply to. It’s optional. If it is not provides, it will be treated as $[0,1,...,len(starts)-1]$.
starts (list|tuple|Tensor) – The data type is int32 . If starts is a list or tuple, the elements of it should be integers or Tensors with shape []. If starts is an Tensor, it should be an 1-D Tensor. It represents starting indices of corresponding axis in axes.
ends (list|tuple|Tensor) – The data type is int32 . If ends is a list or tuple, the elements of it should be integers or Tensors with shape []. If ends is an Tensor, it should be an 1-D Tensor. It represents ending indices of corresponding axis in axes.
strides (list|tuple|Tensor) – The data type is int32 . If strides is a list or tuple, the elements of it should be integers or Tensors with shape []. If strides is an Tensor, it should be an 1-D Tensor. It represents slice step of corresponding axis in axes.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

Tensor, A Tensor with the same dimension as x. The data type is same as x.

Examples

>>> import paddle
>>> x = paddle.zeros(shape=[3,4,5,6], dtype="float32")
>>> # example 1:
>>> # attr starts is a list which doesn't contain Tensor.
>>> axes = [1, 2, 3]
>>> starts = [-3, 0, 2]
>>> ends = [3, 2, 4]
>>> strides_1 = [1, 1, 1]
>>> strides_2 = [1, 1, 2]
>>> sliced_1 = paddle.strided_slice(x, axes=axes, starts=starts, ends=ends, strides=strides_1)
>>> # sliced_1 is x[:, 1:3:1, 0:2:1, 2:4:1].
>>> # example 2:
>>> # attr starts is a list which contain tensor Tensor.
>>> minus_3 = paddle.full(shape=[1], fill_value=-3, dtype='int32')
>>> sliced_2 = paddle.strided_slice(x, axes=axes, starts=[minus_3, 0, 2], ends=ends, strides=strides_2)
>>> # sliced_2 is x[:, 1:3:1, 0:2:1, 2:4:2].

strides

Tensor’s strides.

Returns: strides.
Return type: List

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 2, 3])
>>> y = x[1]
>>> print(y.strides)
[]

subtract ( y: Tensor, name: str | None = None ) → Tensor [source] subtract¶

Subtract two tensors element-wise. The equation is:

\[out = x - y\]

Note

paddle.subtract supports broadcasting. If you want know more about broadcasting, please refer to Introduction to Tensor .

Parameters

x (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int16, int32, int64, complex64, complex128.
y (Tensor) – the input tensor, it’s data type should be bfloat16, float16, float32, float64, int16, int32, int64, complex64, complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. A location into which the result is stored. If x, y have different shapes and are “broadcastable”, the resulting tensor shape is the shape of x and y after broadcasting. If x, y have the same shape, its shape is the same as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2], [7, 8]])
>>> y = paddle.to_tensor([[5, 6], [3, 4]])
>>> res = paddle.subtract(x, y)
>>> print(res)
Tensor(shape=[2, 2], dtype=int64, place=Place(cpu), stop_gradient=True,
[[-4, -4],
 [ 4,  4]])

>>> x = paddle.to_tensor([[[1, 2, 3], [1, 2, 3]]])
>>> y = paddle.to_tensor([1, 0, 4])
>>> res = paddle.subtract(x, y)
>>> print(res)
Tensor(shape=[1, 2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[[ 0,  2, -1],
  [ 0,  2, -1]]])

>>> x = paddle.to_tensor([2, float('nan'), 5], dtype='float32')
>>> y = paddle.to_tensor([1, 4, float('nan')], dtype='float32')
>>> res = paddle.subtract(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1. , nan, nan])

>>> x = paddle.to_tensor([5, float('inf'), -float('inf')], dtype='float64')
>>> y = paddle.to_tensor([1, 4, 5], dtype='float64')
>>> res = paddle.subtract(x, y)
>>> print(res)
Tensor(shape=[3], dtype=float64, place=Place(cpu), stop_gradient=True,
[ 4.  ,  inf., -inf.])

subtract_ ( y: Tensor, name: str | None = None ) → Tensor subtract_¶: Inplace version of subtract API, the output Tensor will be inplaced with input x. Please refer to subtract.

sum ( axis: int | Sequence[int] | None = None, dtype: DTypeLike | None = None, keepdim: bool = False, name: str | None = None ) → Tensor [source] sum¶

Computes the sum of tensor elements over the given dimension.

Parameters

x (Tensor) – An N-D Tensor, the data type is bool, bfloat16, float16, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128.
axis (int|list|tuple|None, optional) – The dimensions along which the sum is performed. If None, sum all elements of x and return a Tensor with a single element, otherwise must be in the range $[-rank(x), rank(x))$. If $axis[i] < 0$, the dimension to reduce is $rank + axis[i]$.
dtype (str|paddle.dtype|np.dtype, optional) – The dtype of output Tensor. The default value is None, the dtype of output is the same as input Tensor x.
keepdim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result Tensor will have one fewer dimension than the x unless keepdim is true, default value is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Results of summation operation on the specified axis of input Tensor x, if x.dtype=’bool’, x.dtype=’int32’, it’s data type is ‘int64’, otherwise it’s data type is the same as x.

Return type

Tensor

Examples

>>> import paddle

>>> # x is a Tensor with following elements:
>>> #    [[0.2, 0.3, 0.5, 0.9]
>>> #     [0.1, 0.2, 0.6, 0.7]]
>>> # Each example is followed by the corresponding output tensor.
>>> x = paddle.to_tensor([[0.2, 0.3, 0.5, 0.9],
...                       [0.1, 0.2, 0.6, 0.7]])
>>> out1 = paddle.sum(x)
>>> out1
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
3.50000000)
>>> out2 = paddle.sum(x, axis=0)
>>> out2
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.30000001, 0.50000000, 1.10000002, 1.59999990])
>>> out3 = paddle.sum(x, axis=-1)
>>> out3
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.89999998, 1.60000002])
>>> out4 = paddle.sum(x, axis=1, keepdim=True)
>>> out4
Tensor(shape=[2, 1], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1.89999998],
 [1.60000002]])

>>> # y is a Tensor with shape [2, 2, 2] and elements as below:
>>> #      [[[1, 2], [3, 4]],
>>> #      [[5, 6], [7, 8]]]
>>> # Each example is followed by the corresponding output tensor.
>>> y = paddle.to_tensor([[[1, 2], [3, 4]],
...                       [[5, 6], [7, 8]]])
>>> out5 = paddle.sum(y, axis=[1, 2])
>>> out5
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[10, 26])
>>> out6 = paddle.sum(y, axis=[0, 1])
>>> out6
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[16, 20])

>>> # x is a Tensor with following elements:
>>> #    [[True, True, True, True]
>>> #     [False, False, False, False]]
>>> # Each example is followed by the corresponding output tensor.
>>> x = paddle.to_tensor([[True, True, True, True],
...                       [False, False, False, False]])
>>> out7 = paddle.sum(x)
>>> out7
Tensor(shape=[], dtype=int64, place=Place(cpu), stop_gradient=True,
4)
>>> out8 = paddle.sum(x, axis=0)
>>> out8
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 1, 1, 1])
>>> out9 = paddle.sum(x, axis=1)
>>> out9
Tensor(shape=[2], dtype=int64, place=Place(cpu), stop_gradient=True,
[4, 0])

svd_lowrank ( q: int | None = None, niter: int = 2, M: Tensor | None = None, name: str | None = None ) → tuple[Tensor, Tensor, Tensor] svd_lowrank¶

Return the singular value decomposition (SVD) on a low-rank matrix or batches of such matrices.

If $X$ is the input matrix or a batch of input matrices, the output should satisfies:

\[X \approx U * diag(S) * V^{H}\]

When $M$ is given, the output should satisfies:

\[X - M \approx U * diag(S) * V^{H}\]

Parameters

x (Tensor) – The input tensor. Its shape should be […, N, M], where … is zero or more batch dimensions. N and M can be arbitrary positive number. The data type of x should be float32 or float64.
q (int, optional) – A slightly overestimated rank of $X$. Default value is None, which means the overestimated rank is 6.
niter (int, optional) – The number of iterations to perform. Default: 2.
M (Tensor, optional) – The input tensor’s mean. Its shape should be […, 1, M]. Default value is None.
name (str|None, optional) – Name for the operation. For more information, please refer to Name. Default: None.

Returns

Tensor U, is N x q matrix.
Tensor S, is a vector with length q.
Tensor V, is M x q matrix.

tuple (U, S, V): which is the nearly optimal approximation of a singular value decomposition of the matrix $X$ or $X - M$.

Examples

>>> import paddle
>>> paddle.seed(2024)

>>> x = paddle.randn((5, 5), dtype='float64')
>>> U, S, V = paddle.linalg.svd_lowrank(x)
>>> print(U)
Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True,
[[-0.03586982, -0.17211503,  0.31536566, -0.38225676, -0.85059629],
 [-0.38386839,  0.67754925,  0.23222694,  0.51777188, -0.26749766],
 [-0.85977150, -0.28442378, -0.41412094, -0.08955629, -0.01948348],
 [ 0.18611503,  0.56047358, -0.67717019, -0.39286761, -0.19577062],
 [ 0.27841082, -0.34099254, -0.46535957,  0.65071250, -0.40770727]])

>>> print(S)
Tensor(shape=[5], dtype=float64, place=Place(cpu), stop_gradient=True,
[4.11253399, 3.03227120, 2.45499752, 1.25602436, 0.45825337])

>>> print(V)
Tensor(shape=[5, 5], dtype=float64, place=Place(cpu), stop_gradient=True,
[[ 0.46401347,  0.50977695, -0.08742316, -0.11140428, -0.71046833],
 [-0.48927226, -0.35047624,  0.07918771,  0.45431083, -0.65200463],
 [-0.20494730,  0.67097011, -0.05427719,  0.66510472,  0.24997083],
 [-0.69645001,  0.40237917,  0.09360970, -0.58032322, -0.08666357],
 [ 0.13512270,  0.07199989,  0.98710572,  0.04529277,  0.01134594]])

t ( name: str | None = None ) → Tensor [source] t¶

Transpose <=2-D tensor. 0-D and 1-D tensors are returned as it is and 2-D tensor is equal to the paddle.transpose function which perm dimensions set 0 and 1.

Parameters

input (Tensor) – The input Tensor. It is a N-D (N<=2) Tensor of data types float32, float64, int32, int64.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

A transposed n-D Tensor, with data type being float16, float32, float64, int32, int64.

Return type

Tensor

Examples

>>> import paddle

>>> # Example 1 (0-D tensor)
>>> x = paddle.to_tensor([0.79])
>>> out = paddle.t(x)
>>> print(out)
Tensor(shape=[1], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.79000002])

>>> # Example 2 (1-D tensor)
>>> x = paddle.to_tensor([0.79, 0.84, 0.32])
>>> out2 = paddle.t(x)
>>> print(out2)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[0.79000002, 0.83999997, 0.31999999])
>>> print(paddle.t(x).shape)
[3]

>>> # Example 3 (2-D tensor)
>>> x = paddle.to_tensor([[0.79, 0.84, 0.32],
...                       [0.64, 0.14, 0.57]])
>>> print(x.shape)
[2, 3]
>>> out3 = paddle.t(x)
>>> print(out3)
Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0.79000002, 0.63999999],
 [0.83999997, 0.14000000],
 [0.31999999, 0.56999999]])
>>> print(paddle.t(x).shape)
[3, 2]

t_ ( name=None ) [source] t_¶: Inplace version of t API, the output Tensor will be inplaced with input input. Please refer to t.

take ( index: Tensor, mode: Literal['raise', 'wrap', 'clip'] = 'raise', name: str | None = None ) → Tensor [source] take¶

Returns a new tensor with the elements of input tensor x at the given index. The input tensor is treated as if it were viewed as a 1-D tensor. The result takes the same shape as the index.

Parameters

x (Tensor) – An N-D Tensor, its data type should be int32, int64, float32, float64.
index (Tensor) – An N-D Tensor, its data type should be int32, int64.
mode (str, optional) –
Specifies how out-of-bounds index will behave. the candidates are 'raise', 'wrap' and 'clip'.
- 'raise': raise an error (default);
- 'wrap': wrap around;
- 'clip': clip to the range. 'clip' mode means that all indices that are too large are replaced by the index that addresses the last element. Note that this disables indexing with negative numbers.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Tensor with the same shape as index, the data type is the same with input.

Examples

>>> import paddle

>>> x_int = paddle.arange(0, 12).reshape([3, 4])
>>> x_float = x_int.astype(paddle.float64)

>>> idx_pos = paddle.arange(4, 10).reshape([2, 3])  # positive index
>>> idx_neg = paddle.arange(-2, 4).reshape([2, 3])  # negative index
>>> idx_err = paddle.arange(-2, 13).reshape([3, 5])  # index out of range

>>> paddle.take(x_int, idx_pos)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[4, 5, 6],
 [7, 8, 9]])

>>> paddle.take(x_int, idx_neg)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[10, 11, 0 ],
 [1 , 2 , 3 ]])

>>> paddle.take(x_float, idx_pos)
Tensor(shape=[2, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[4., 5., 6.],
 [7., 8., 9.]])

>>> x_int.take(idx_pos)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[4, 5, 6],
 [7, 8, 9]])

>>> paddle.take(x_int, idx_err, mode='wrap')
Tensor(shape=[3, 5], dtype=int64, place=Place(cpu), stop_gradient=True,
[[10, 11, 0 , 1 , 2 ],
 [3 , 4 , 5 , 6 , 7 ],
 [8 , 9 , 10, 11, 0 ]])

>>> paddle.take(x_int, idx_err, mode='clip')
Tensor(shape=[3, 5], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0 , 0 , 0 , 1 , 2 ],
 [3 , 4 , 5 , 6 , 7 ],
 [8 , 9 , 10, 11, 11]])

take_along_axis ( indices: Tensor, axis: int, broadcast: bool = True ) → Tensor [source] take_along_axis¶

Take values from the input array by given indices matrix along the designated axis.

Parameters

arr (Tensor) – The input Tensor. Supported data types are bfloat16, float16, float32, float64, int32, int64, uint8.
indices (Tensor) – Indices to take along each 1d slice of arr. This must match the dimension of arr, and need to broadcast against arr. Supported data type are int32 and int64.
axis (int) – The axis to take 1d slices along.
broadcast (bool, optional) – whether the indices broadcast.

Returns

Tensor, The indexed element, same dtype with arr

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1, 2, 3], [4, 5, 6], [7,8,9]])
>>> index = paddle.to_tensor([[0]])
>>> axis = 0
>>> result = paddle.take_along_axis(x, index, axis)
>>> print(result)
Tensor(shape=[1, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 2, 3]])

tan ( name: str | None = None ) → Tensor [source] tan¶

Tangent Operator. Computes tangent of x element-wise.

Input range is (k*pi-pi/2, k*pi+pi/2) and output range is (-inf, inf).

\[out = tan(x)\]

Parameters

x (Tensor) – Input of Tan operator, an N-D Tensor, with data type float32, float64, float16, bfloat16, uint8, int8, int16, int32, int64, complex64 or complex128.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor. Output of Tan operator, a Tensor with shape same as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.tan(x)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.42279324, -0.20271003,  0.10033467,  0.30933627])

tan_ ( name=None ) tan_¶: Inplace version of tan API, the output Tensor will be inplaced with input x. Please refer to tan.

tanh ( name: str | None = None ) → Tensor [source] tanh¶

Tanh Activation Operator.

\[out = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]

Parameters

x (Tensor) – Input of Tanh operator, an N-D Tensor, with data type bfloat16, float32, float64, float16, uint8, int8, int16, int32, int64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Output of Tanh operator, a Tensor with same data type and shape as input: (integer types are autocasted into float32).

Examples

>>> import paddle

>>> x = paddle.to_tensor([-0.4, -0.2, 0.1, 0.3])
>>> out = paddle.tanh(x)
>>> out
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[-0.37994900, -0.19737528,  0.09966799,  0.29131261])

tanh_ ( name: str | None = None ) → Tensor [source] tanh_¶: Inplace version of tanh API, the output Tensor will be inplaced with input x. Please refer to tanh.

tensor_split ( num_or_indices: int | Sequence[int], axis: int | Tensor = 0, name: str | None = None ) → list[Tensor] [source] tensor_split¶

Split the input tensor into multiple sub-Tensors along axis, allowing not being of equal size.

In the following figure, the shape of Tenser x is [6], and after paddle.tensor_split(x, num_or_indices=4) transformation, we get four sub-Tensors out0, out1, out2, and out3 :

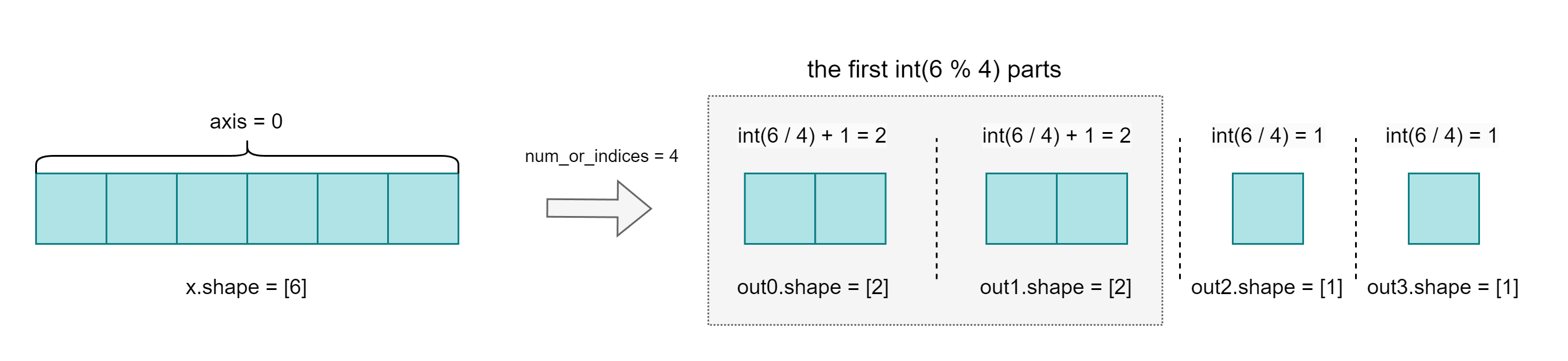
https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/tensor_split/tensor_split-1_en.png

since the length of x in axis = 0 direction 6 is not divisible by num_or_indices = 4, the size of the first int(6 % 4) part after splitting will be int(6 / 4) + 1 and the size of the remaining parts will be int(6 / 4).

Parameters

x (Tensor) – A Tensor whose dimension must be greater than 0. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If num_or_indices is an int n, x is split into n sections along axis. If x is divisible by n, each section will be x.shape[axis] / n. If x is not divisible by n, the first int(x.shape[axis] % n) sections will have size int(x.shape[axis] / n) + 1, and the rest will be int(x.shape[axis] / n). If ``num_or_indices is a list or tuple of integer indices, x is split along axis at each of the indices. For instance, num_or_indices=[2, 4] with axis=0 would split x into x[:2], x[2:4] and x[4:] along axis 0.
axis (int|Tensor, optional) – The axis along which to split, it can be a integer or a 0-D Tensor with shape [] and data type int32 or int64. If :math::axis < 0, the axis to split along is $rank(x) + axis$. Default is 0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

list[Tensor], The list of segmented Tensors.

Examples

>>> import paddle

>>> # evenly split
>>> # x is a Tensor of shape [8]
>>> x = paddle.rand([8])
>>> out0, out1 = paddle.tensor_split(x, num_or_indices=2)
>>> print(out0.shape)
[4]
>>> print(out1.shape)
[4]

https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/tensor_split/tensor_split-2.png

>>> import paddle

>>> # not evenly split
>>> # x is a Tensor of shape [8]
>>> x = paddle.rand([8])
>>> out0, out1, out2 = paddle.tensor_split(x, num_or_indices=3)
>>> print(out0.shape)
[3]
>>> print(out1.shape)
[3]
>>> print(out2.shape)
[2]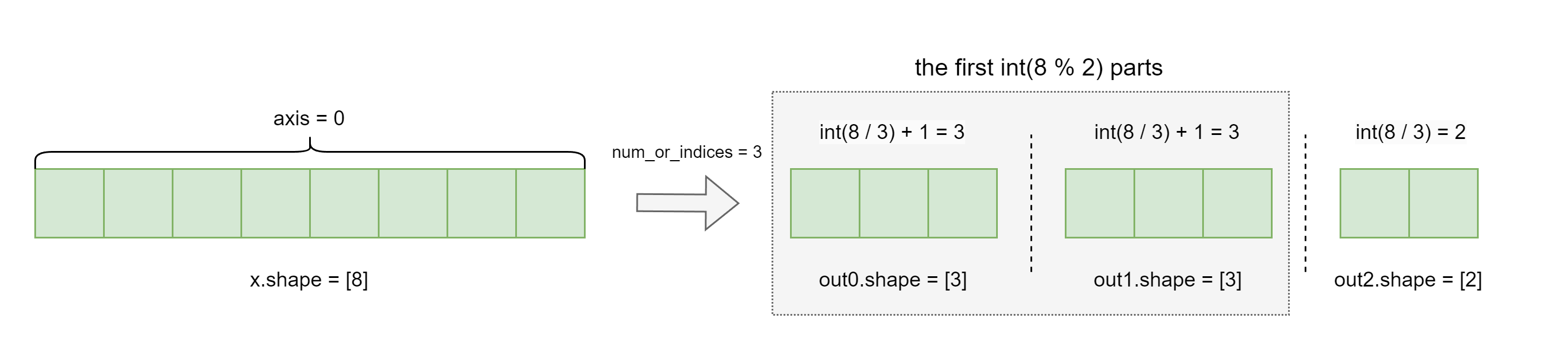

https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/tensor_split/tensor_split-3_en.png

>>> import paddle

>>> # split with indices
>>> # x is a Tensor of shape [8]
>>> x = paddle.rand([8])
>>> out0, out1, out2 = paddle.tensor_split(x, num_or_indices=[2, 3])
>>> print(out0.shape)
[2]
>>> print(out1.shape)
[1]
>>> print(out2.shape)
[5]

https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/tensor_split/tensor_split-4.png

>>> import paddle

>>> # split along axis
>>> # x is a Tensor of shape [7, 8]
>>> x = paddle.rand([7, 8])
>>> out0, out1 = paddle.tensor_split(x, num_or_indices=2, axis=1)
>>> print(out0.shape)
[7, 4]
>>> print(out1.shape)
[7, 4]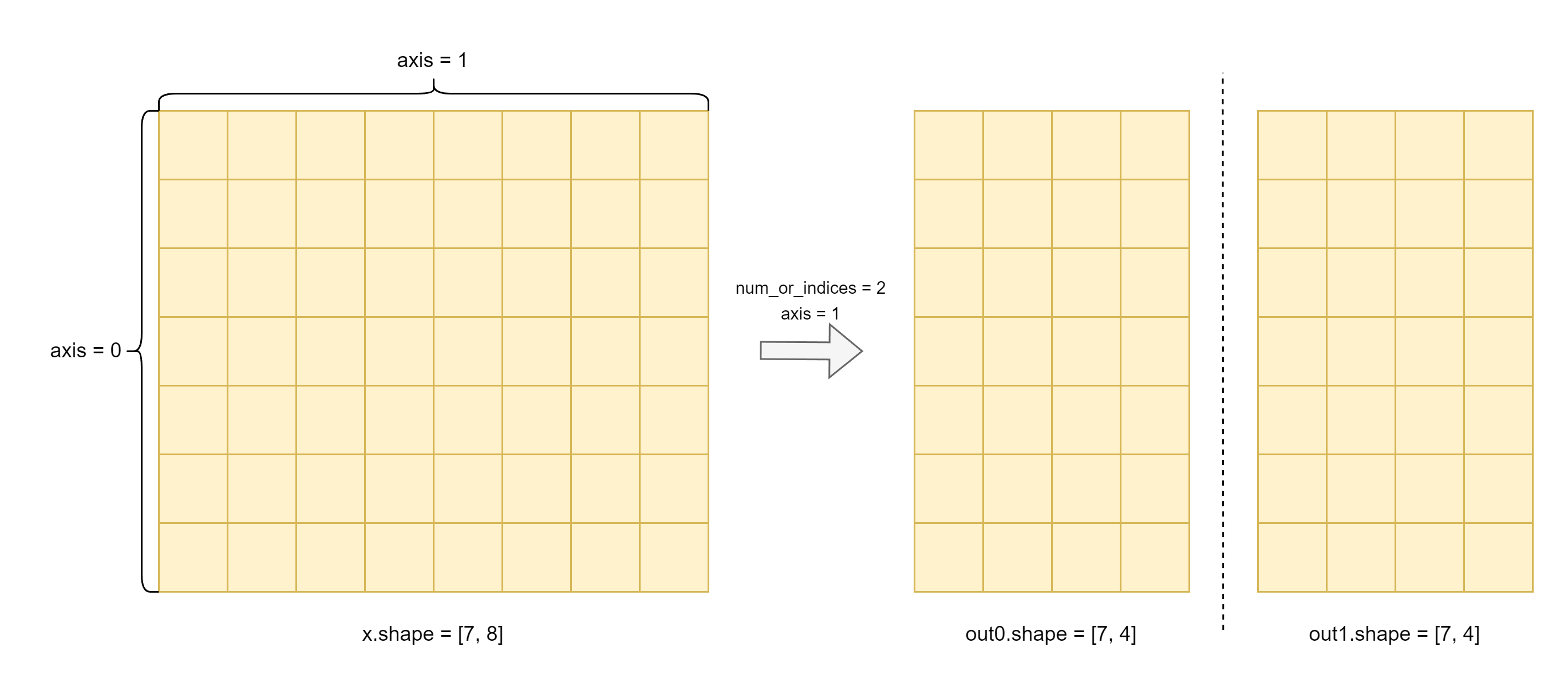

https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/tensor_split/tensor_split-5.png

>>> import paddle

>>> # split along axis with indices
>>> # x is a Tensor of shape [7, 8]
>>> x = paddle.rand([7, 8])
>>> out0, out1, out2 = paddle.tensor_split(x, num_or_indices=[2, 3], axis=1)
>>> print(out0.shape)
[7, 2]
>>> print(out1.shape)
[7, 1]
>>> print(out2.shape)
[7, 5]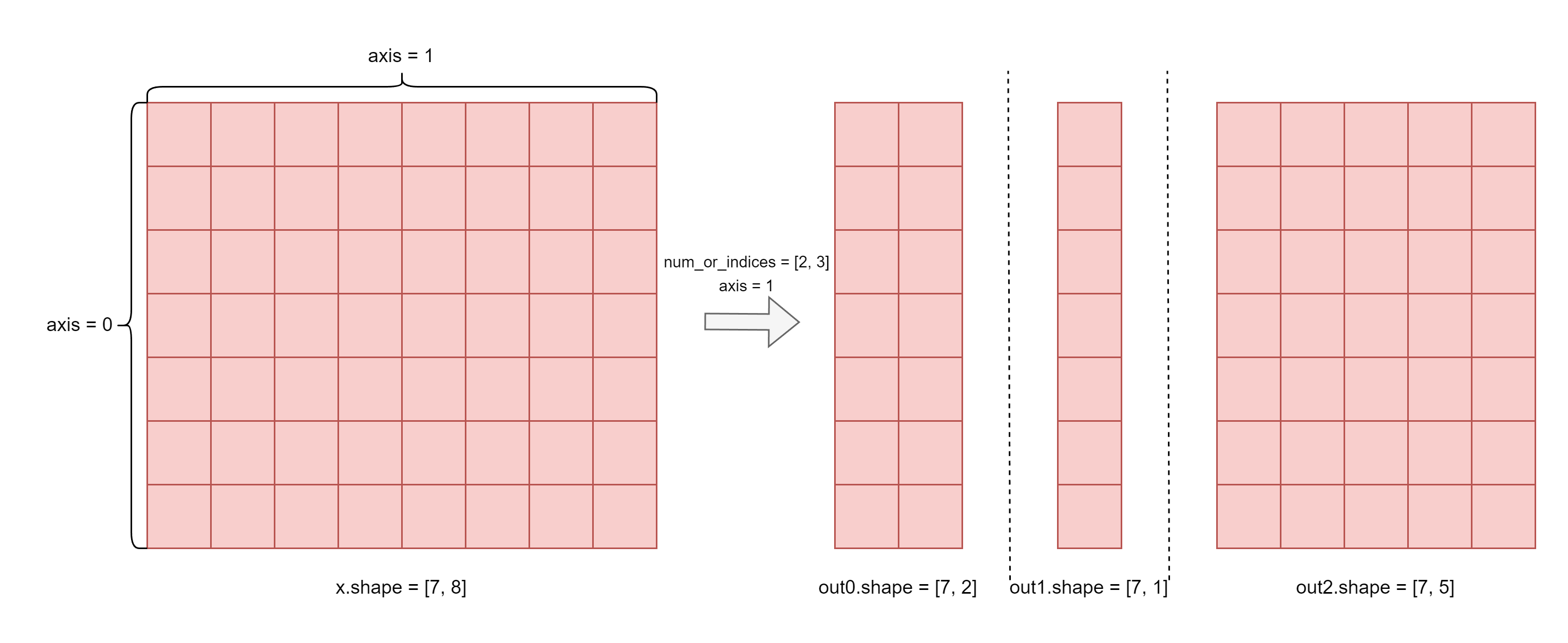

https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/tensor_split/tensor_split-6.png

tensordot ( y: Tensor, axes: int | NestedSequence[int] | Tensor = 2, name: str | None = None ) → Tensor [source] tensordot¶

This function computes a contraction, which sum the product of elements from two tensors along the given axes.

Parameters

x (Tensor) – The left tensor for contraction with data type float16 or float32 or float64.
y (Tensor) – The right tensor for contraction with the same data type as x.
axes (int|tuple|list|Tensor, optional) –
The axes to contract for x and y, defaulted to integer 2.
1. It could be a non-negative integer n, in which the function will sum over the last n axes of x and the first n axes of y in order.
2. It could be a 1-d tuple or list with data type int, in which x and y will be contracted along the same given axes. For example, axes =[0, 1] applies contraction along the first two axes for x and the first two axes for y.
3. It could be a tuple or list containing one or two 1-d tuple|list|Tensor with data type int. When containing one tuple|list|Tensor, the data in tuple|list|Tensor specified the same axes for x and y to contract. When containing two tuple|list|Tensor, the first will be applied to x and the second to y. When containing more than two tuple|list|Tensor, only the first two axis sequences will be used while the others will be ignored.
4. It could be a tensor, in which the axes tensor will be translated to a python list and applied the same rules described above to determine the contraction axes. Note that the axes with Tensor type is ONLY available in Dygraph mode.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

Output (Tensor), The contraction result with the same data type as x and y. In general, $output.ndim = x.ndim + y.ndim - 2 \times n_{axes}$, where $n_{axes}$ denotes the number of axes to be contracted.

Notes

This function supports tensor broadcast, the size in the corresponding dimensions of x and y should be equal, or applies to the broadcast rules.
This function also supports axes expansion, when the two given axis sequences for x and y are of different lengths, the shorter sequence will expand the same axes as the longer one at the end. For example, if axes =[[0, 1, 2, 3], [1, 0]], the axis sequence for x is [0, 1, 2, 3], while the corresponding axis sequences for y will be expanded from [1, 0] to [1, 0, 2, 3].

Examples

>>> import paddle
>>> from typing import Literal

>>> data_type: Literal["float64"] = 'float64'

>>> # For two 2-d tensor x and y, the case axes=0 is equivalent to outer product.
>>> # Note that tensordot supports empty axis sequence, so all the axes=0, axes=[], axes=[[]], and axes=[[],[]] are equivalent cases.
>>> x = paddle.arange(4, dtype=data_type).reshape([2, 2])
>>> y = paddle.arange(4, dtype=data_type).reshape([2, 2])
>>> z = paddle.tensordot(x, y, axes=0)
>>> print(z)
Tensor(shape=[2, 2, 2, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
 [[[[0., 0.],
    [0., 0.]],
   [[0., 1.],
    [2., 3.]]],
  [[[0., 2.],
    [4., 6.]],
   [[0., 3.],
    [6., 9.]]]])

>>> # For two 1-d tensor x and y, the case axes=1 is equivalent to inner product.
>>> x = paddle.arange(10, dtype=data_type)
>>> y = paddle.arange(10, dtype=data_type)
>>> z1 = paddle.tensordot(x, y, axes=1)
>>> z2 = paddle.dot(x, y)
>>> print(z1)
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=True,
285.)
>>> print(z2)
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=True,
285.)


>>> # For two 2-d tensor x and y, the case axes=1 is equivalent to matrix multiplication.
>>> x = paddle.arange(6, dtype=data_type).reshape([2, 3])
>>> y = paddle.arange(12, dtype=data_type).reshape([3, 4])
>>> z1 = paddle.tensordot(x, y, axes=1)
>>> z2 = paddle.matmul(x, y)
>>> print(z1)
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=True,
[[20., 23., 26., 29.],
 [56., 68., 80., 92.]])
>>> print(z2)
Tensor(shape=[2, 4], dtype=float64, place=Place(cpu), stop_gradient=True,
[[20., 23., 26., 29.],
 [56., 68., 80., 92.]])

>>> # When axes is a 1-d int list, x and y will be contracted along the same given axes.
>>> # Note that axes=[1, 2] is equivalent to axes=[[1, 2]], axes=[[1, 2], []], axes=[[1, 2], [1]], and axes=[[1, 2], [1, 2]].
>>> x = paddle.arange(24, dtype=data_type).reshape([2, 3, 4])
>>> y = paddle.arange(36, dtype=data_type).reshape([3, 3, 4])
>>> z = paddle.tensordot(x, y, axes=[1, 2])
>>> print(z)
Tensor(shape=[2, 3], dtype=float64, place=Place(cpu), stop_gradient=True,
[[506. , 1298., 2090.],
 [1298., 3818., 6338.]])

>>> # When axes is a list containing two 1-d int list, the first will be applied to x and the second to y.
>>> x = paddle.arange(60, dtype=data_type).reshape([3, 4, 5])
>>> y = paddle.arange(24, dtype=data_type).reshape([4, 3, 2])
>>> z = paddle.tensordot(x, y, axes=([1, 0], [0, 1]))
>>> print(z)
Tensor(shape=[5, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[4400., 4730.],
 [4532., 4874.],
 [4664., 5018.],
 [4796., 5162.],
 [4928., 5306.]])

>>> # Thanks to the support of axes expansion, axes=[[0, 1, 3, 4], [1, 0, 3, 4]] can be abbreviated as axes= [[0, 1, 3, 4], [1, 0]].
>>> x = paddle.arange(720, dtype=data_type).reshape([2, 3, 4, 5, 6])
>>> y = paddle.arange(720, dtype=data_type).reshape([3, 2, 4, 5, 6])
>>> z = paddle.tensordot(x, y, axes=[[0, 1, 3, 4], [1, 0]])
>>> print(z)
Tensor(shape=[4, 4], dtype=float64, place=Place(cpu), stop_gradient=True,
[[23217330., 24915630., 26613930., 28312230.],
 [24915630., 26775930., 28636230., 30496530.],
 [26613930., 28636230., 30658530., 32680830.],
 [28312230., 30496530., 32680830., 34865130.]])

tile ( repeat_times: TensorOrTensors | Sequence[int], name: str | None = None ) → Tensor [source] tile¶

Construct a new Tensor by repeating x the number of times given by repeat_times. After tiling, the value of the i’th dimension of the output is equal to x.shape[i]*repeat_times[i].

Both the number of dimensions of x and the number of elements in repeat_times should be less than or equal to 6.

Parameters

x (Tensor) – The input tensor, its data type should be bool, float16, float32, float64, int32, int64, complex64 or complex128.
repeat_times (list|tuple|Tensor) – The number of repeating times. If repeat_times is a list or tuple, all its elements should be integers or 1-D Tensors with the data type int32. If repeat_times is a Tensor, it should be an 1-D Tensor with the data type int32.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

N-D Tensor. The data type is the same as x. The size of the i-th dimension is equal to x[i] * repeat_times[i].

Examples

>>> import paddle

>>> data = paddle.to_tensor([1, 2, 3], dtype='int32')
>>> out = paddle.tile(data, repeat_times=[2, 1])
>>> print(out)
Tensor(shape=[2, 3], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 2, 3],
 [1, 2, 3]])

>>> out = paddle.tile(data, repeat_times=(2, 2))
>>> print(out)
Tensor(shape=[2, 6], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 2, 3, 1, 2, 3],
 [1, 2, 3, 1, 2, 3]])

>>> repeat_times = paddle.to_tensor([1, 2], dtype='int32')
>>> out = paddle.tile(data, repeat_times=repeat_times)
>>> print(out)
Tensor(shape=[1, 6], dtype=int32, place=Place(cpu), stop_gradient=True,
[[1, 2, 3, 1, 2, 3]])

to ( *args, **kwargs )
to¶

Performs Tensor dtype and/or device conversion. A paddle.dtype and place are inferred from the arguments of self.to(*args, **kwargs).There are three ways to call to:

to(dtype, blocking=True)

to(device, dtype=None, blocking=True)

to(other, blocking=True)

Notes:: If the self Tensor already has the correct dtype and device, then self is returned. Otherwise, the returned tensor is a copy of self with the desired dtype and device.

Returns: self
Return type: Tensor

Examples

>>> import paddle
>>> x = paddle.to_tensor([1,2,3])
>>> print(x)
Tensor(shape=[3], dtype=int64, place=Place(gpu:0), stop_gradient=True,
    [1, 2, 3])

>>> x = x.to("cpu")
>>> print(x.place)
Place(cpu)

>>> x = x.to("float32")
>>> print(x.dtype)
paddle.float32

>>> x = x.to("gpu", "int16")
>>> print(x)
Tensor(shape=[3], dtype=int16, place=Place(gpu:0), stop_gradient=True,
    [1, 2, 3])
>>> y = paddle.to_tensor([4,5,6])
>>> y
Tensor(shape=[3], dtype=int64, place=Place(gpu:0), stop_gradient=True,
    [4, 5, 6])
>>> y = y.to(x)
>>> print(y)
Tensor(shape=[3], dtype=int16, place=Place(gpu:0), stop_gradient=True,
    [4, 5, 6])

to_dense ( ) → Tensor to_dense¶

Notes:: This API is ONLY available in Dygraph mode

Convert the current SparseTensor(COO or CSR) to DenseTensor.

Returns: A DenseTensor
Return type: Tensor

Examples

>>> import paddle
>>> indices = [[0, 0, 1, 2, 2], [1, 3, 2, 0, 1]]
>>> values = [1, 2, 3, 4, 5]
>>> dense_shape = [3, 4]
>>> sparse_x = paddle.sparse.sparse_coo_tensor(paddle.to_tensor(indices, dtype='int64'), paddle.to_tensor(values, dtype='float32'), shape=dense_shape)
>>> dense_x = sparse_x.to_dense()
>>> print(dense_x)
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[0., 1., 0., 2.],
 [0., 0., 3., 0.],
 [4., 5., 0., 0.]])

to_sparse_coo ( sparse_dim: int ) → Tensor to_sparse_coo¶

Notes:: This API is ONLY available in Dygraph mode

Convert the current DenseTensor to SparseTensor in COO format.

Returns: A SparseCooTensor
Return type: Tensor

Examples

>>> import paddle
>>> dense_x = [[0, 1, 0, 2], [0, 0, 3, 4]]
>>> dense_x = paddle.to_tensor(dense_x, dtype='float32')
>>> sparse_x = dense_x.to_sparse_coo(sparse_dim=2)
>>> print(sparse_x)
Tensor(shape=[2, 4], dtype=paddle.float32, place=Place(cpu), stop_gradient=True,
       indices=[[0, 0, 1, 1],
                [1, 3, 2, 3]],
       values=[1., 2., 3., 4.])

to_sparse_csr ( ) to_sparse_csr¶

Note

This API is only available for DenseTensor or SparseCooTensor.

Convert input Tensor to SparseCsrTensor.

When input is SparseCooTensor, will convert COO to CSR . When input is DenseTensor, will convert Dense to CSR .

Returns: SparseCsrTensor

Examples

>>> import paddle

>>> indices = [[0, 1, 2], [1, 2, 0]]
>>> values = [1.0, 2.0, 3.0]
>>> dense_shape = [3, 3]
>>> coo = paddle.sparse.sparse_coo_tensor(indices, values, dense_shape)
>>> coo.to_sparse_csr()
Tensor(shape=[3, 3], dtype=paddle.float32, place=Place(gpu:0), stop_gradient=True,
crows=[0, 1, 2, 3],
cols=[1, 2, 0],
values=[1., 2., 3.])

tolist ( ) → NestedList[int | float | complex] [source] tolist¶

Note

This API is ONLY available in Dygraph mode.

This function translate the paddle.Tensor to python list.

Parameters: x (Tensor) – x is the Tensor we want to translate to list.
Returns: list, A list that contain the same value of current Tensor.

Examples

>>> import paddle

>>> t = paddle.to_tensor([0,1,2,3,4])
>>> expectlist = t.tolist()
>>> print(expectlist)
[0, 1, 2, 3, 4]

>>> expectlist = paddle.tolist(t)
>>> print(expectlist)
[0, 1, 2, 3, 4]

top_p_sampling ( ps: Tensor, threshold: Tensor | None = None, topp_seed: Tensor | None = None, seed: int = -1, k: int = 0, mode: Literal['truncated', 'non-truncated'] = 'truncated', return_top: bool = False, name: str | None = None ) → tuple[Tensor, Tensor] top_p_sampling¶

Get the TopP scores and ids.

Parameters

x (Tensor) – An input 2-D Tensor with type float32, float16 and bfloat16.
ps (Tensor) – A 1-D Tensor with type float32, float16 and bfloat16, used to specify the top_p corresponding to each query.
threshold (Tensor|None, optional) – A 1-D Tensor with type float32, float16 and bfloat16, used to avoid sampling low score tokens.
topp_seed (Tensor|None, optional) – A 1-D Tensor with type int64, used to specify the random seed for each query.
seed (int, optional) – the random seed. Default is -1,
k (int) – the number of top_k scores/ids to be returned. Default is 0.
mode (str) – The mode to choose sampling strategy. If the mode is truncated, sampling will truncate the probability at top_p_value. If the mode is non-truncated, it will not be truncated. Default is truncated.
return_top (bool) – Whether to return the top_k scores and ids. Default is False.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

tuple(Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.

Examples

>>> 
>>> import paddle

>>> paddle.device.set_device('gpu')
>>> paddle.seed(2023)
>>> x = paddle.randn([2,3])
>>> print(x)
Tensor(shape=[2, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
 [[-0.32012719, -0.07942779,  0.26011357],
  [ 0.79003978, -0.39958701,  1.42184138]])
>>> paddle.seed(2023)
>>> ps = paddle.randn([2])
>>> print(ps)
Tensor(shape=[2], dtype=float32, place=Place(gpu:0), stop_gradient=True,
 [-0.32012719, -0.07942779])
>>> value, index = paddle.tensor.top_p_sampling(x, ps)
>>> print(value)
Tensor(shape=[2, 1], dtype=float32, place=Place(gpu:0), stop_gradient=True,
 [[0.26011357],
  [1.42184138]])
>>> print(index)
Tensor(shape=[2, 1], dtype=int64, place=Place(gpu:0), stop_gradient=True,
 [[2],
  [2]])

topk ( k: int | Tensor, axis: int | None = None, largest: bool = True, sorted: bool = True, name: str | None = None ) → tuple[Tensor, Tensor] [source] topk¶

Return values and indices of the k largest or smallest at the optional axis. If the input is a 1-D Tensor, finds the k largest or smallest values and indices. If the input is a Tensor with higher rank, this operator computes the top k values and indices along the axis.

Parameters

x (Tensor) – Tensor, an input N-D Tensor with type float32, float64, int32, int64.
k (int, Tensor) – The number of top elements to look for along the axis.
axis (int|None, optional) – Axis to compute indices along. The effective range is [-R, R), where R is x.ndim. when axis < 0, it works the same way as axis + R. Default is -1.
largest (bool, optional) – largest is a flag, if set to true, algorithm will sort by descending order, otherwise sort by ascending order. Default is True.
sorted (bool, optional) – controls whether to return the elements in sorted order, default value is True.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

tuple(Tensor), return the values and indices. The value data type is the same as the input x. The indices data type is int64.

Examples

>>> import paddle

>>> data_1 = paddle.to_tensor([1, 4, 5, 7])
>>> value_1, indices_1 = paddle.topk(data_1, k=1)
>>> print(value_1)
Tensor(shape=[1], dtype=int64, place=Place(cpu), stop_gradient=True,
[7])
>>> print(indices_1)
Tensor(shape=[1], dtype=int64, place=Place(cpu), stop_gradient=True,
[3])

>>> data_2 = paddle.to_tensor([[1, 4, 5, 7], [2, 6, 2, 5]])
>>> value_2, indices_2 = paddle.topk(data_2, k=1)
>>> print(value_2)
Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[7],
 [6]])
>>> print(indices_2)
Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3],
 [1]])

>>> value_3, indices_3 = paddle.topk(data_2, k=1, axis=-1)
>>> print(value_3)
Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[7],
 [6]])
>>> print(indices_3)
Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[3],
 [1]])

>>> value_4, indices_4 = paddle.topk(data_2, k=1, axis=0)
>>> print(value_4)
Tensor(shape=[1, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[2, 6, 5, 7]])
>>> print(indices_4)
Tensor(shape=[1, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1, 1, 0, 0]])

trace ( offset: int = 0, axis1: int = 0, axis2: int = 1, name: str | None = None ) → Tensor [source] trace¶

Computes the sum along diagonals of the input tensor x.

If x is 2D, returns the sum of diagonal.

If x has larger dimensions, then returns an tensor of diagonals sum, diagonals be taken from the 2D planes specified by axis1 and axis2. By default, the 2D planes formed by the first and second axes of the input tensor x.

The argument offset determines where diagonals are taken from input tensor x:

If offset = 0, it is the main diagonal.
If offset > 0, it is above the main diagonal.
If offset < 0, it is below the main diagonal.
Note that if offset is out of input’s shape indicated by axis1 and axis2, 0 will be returned.

Parameters

x (Tensor) – The input tensor x. Must be at least 2-dimensional. The input data type should be float16, float32, float64, int32, int64.
offset (int, optional) – Which diagonals in input tensor x will be taken. Default: 0 (main diagonals).
axis1 (int, optional) – The first axis with respect to take diagonal. Default: 0.
axis2 (int, optional) – The second axis with respect to take diagonal. Default: 1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

the output data type is the same as input data type.

Return type

Tensor

Examples

>>> import paddle

>>> case1 = paddle.randn([2, 3])
>>> case2 = paddle.randn([3, 10, 10])
>>> case3 = paddle.randn([3, 10, 5, 10])
>>> data1 = paddle.trace(case1)
>>> data1.shape
[]
>>> data2 = paddle.trace(case2, offset=1, axis1=1, axis2=2)
>>> data2.shape
[3]
>>> data3 = paddle.trace(case3, offset=-3, axis1=1, axis2=-1)
>>> data3.shape
[3, 5]

transpose ( perm: Sequence[int], name: str | None = None ) → Tensor [source] transpose¶

Permute the data dimensions of input according to perm.

The i-th dimension of the returned tensor will correspond to the perm[i]-th dimension of input.

Parameters

x (Tensor) – The input Tensor. It is a N-D Tensor of data types bool, float16, bfloat16, float32, float64, int8, int16, int32, int64, uint8, uint16, complex64, complex128.
perm (list|tuple) – Permute the input according to the data of perm.
name (str|None, optional) – The name of this layer. For more information, please refer to Name. Default is None.

Returns

A transposed n-D Tensor, with data type being bool, float32, float64, int32, int64.

Return type

Tensor

Examples

# The following codes in this code block are pseudocode, designed to show the execution logic and results of the function.

x = to_tensor([[[ 1  2  3  4] [ 5  6  7  8] [ 9 10 11 12]]
               [[13 14 15 16] [17 18 19 20] [21 22 23 24]]])
shape(x): return [2,3,4]

# Example 1
perm0 = [1,0,2]
y_perm0 = transpose(x, perm0) # Permute x by perm0

# dim:0 of y_perm0 is dim:1 of x
# dim:1 of y_perm0 is dim:0 of x
# dim:2 of y_perm0 is dim:2 of x
# The above two lines can also be understood as exchanging the zeroth and first dimensions of x

y_perm0.data = [[[ 1  2  3  4]  [13 14 15 16]]
                [[ 5  6  7  8]  [17 18 19 20]]
                [[ 9 10 11 12]  [21 22 23 24]]]
shape(y_perm0): return [3,2,4]

# Example 2
perm1 = [2,1,0]
y_perm1 = transpose(x, perm1) # Permute x by perm1

# dim:0 of y_perm1 is dim:2 of x
# dim:1 of y_perm1 is dim:1 of x
# dim:2 of y_perm1 is dim:0 of x
# The above two lines can also be understood as exchanging the zeroth and second dimensions of x

y_perm1.data = [[[ 1 13]  [ 5 17]  [ 9 21]]
                [[ 2 14]  [ 6 18]  [10 22]]
                [[ 3 15]  [ 7 19]  [11 23]]
                [[ 4 16]  [ 8 20]  [12 24]]]
shape(y_perm1): return [4,3,2]

Examples

>>> import paddle

>>> x = paddle.randn([2, 3, 4])
>>> x_transposed = paddle.transpose(x, perm=[1, 0, 2])
>>> print(x_transposed.shape)
[3, 2, 4]

transpose_ ( perm, name=None ) [source] transpose_¶: Inplace version of transpose API, the output Tensor will be inplaced with input x. Please refer to transpose.

trapezoid ( x: Tensor | None = None, dx: float | None = None, axis: int = -1, name: str | None = None ) → Tensor [source] trapezoid¶

Integrate along the given axis using the composite trapezoidal rule. Use the sum method.

Parameters

y (Tensor) – Input tensor to integrate. It’s data type should be float16, float32, float64.
x (Tensor|None, optional) – The sample points corresponding to the y values, the same type as y. It is known that the size of y is [d_1, d_2, … , d_n] and $axis=k$, then the size of x can only be [d_k] or [d_1, d_2, … , d_n ]. If x is None, the sample points are assumed to be evenly spaced dx apart. The default is None.
dx (float|None, optional) – The spacing between sample points when x is None. If neither x nor dx is provided then the default is $dx = 1$.
axis (int, optional) – The axis along which to integrate. The default is -1.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, Definite integral of y is N-D tensor as approximated along a single axis by the trapezoidal rule. If y is a 1D tensor, then the result is a float. If N is greater than 1, then the result is an (N-1)-D tensor.

Examples

>>> import paddle

>>> y = paddle.to_tensor([4, 5, 6], dtype='float32')

>>> paddle.trapezoid(y)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
10.)

>>> paddle.trapezoid(y, dx=2.)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
20.)

>>> y = paddle.to_tensor([4, 5, 6], dtype='float32')
>>> x = paddle.to_tensor([1, 2, 3], dtype='float32')

>>> paddle.trapezoid(y, x)
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
10.)

>>> y = paddle.to_tensor([1, 2, 3], dtype='float64')
>>> x = paddle.to_tensor([8, 6, 4], dtype='float64')

>>> paddle.trapezoid(y, x)
Tensor(shape=[], dtype=float64, place=Place(cpu), stop_gradient=True,
-8.)
>>> y = paddle.arange(6).reshape((2, 3)).astype('float32')

>>> paddle.trapezoid(y, axis=0)
Tensor(shape=[3], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.50000000, 2.50000000, 3.50000000])
>>> paddle.trapezoid(y, axis=1)
Tensor(shape=[2], dtype=float32, place=Place(cpu), stop_gradient=True,
[2., 8.])

tril ( diagonal: int = 0, name: Optional[str] = None ) → Tensor [source] tril¶

Returns the lower triangular part of a matrix (2-D tensor) or batch of matrices x, the other elements of the result tensor are set to 0. The lower triangular part of the matrix is defined as the elements on and below the diagonal.

Parameters

x (Tensor) – The input x which is a Tensor. Support data types: bool, float64, float32, int32, int64, complex64, complex128.
diagonal (int, optional) – The diagonal to consider, default value is 0. If diagonal = 0, all elements on and below the main diagonal are retained. A positive value includes just as many diagonals above the main diagonal, and similarly a negative value excludes just as many diagonals below the main diagonal. The main diagonal are the set of indices $\{(i, i)\}$ for $i \in [0, \min\{d_{1}, d_{2}\} - 1]$ where $d_{1}, d_{2}$ are the dimensions of the matrix.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Results of lower triangular operation by the specified diagonal of input tensor x, it’s data type is the same as x’s Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> data = paddle.arange(1, 13, dtype="int64").reshape([3,-1])
>>> print(data)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 , 4 ],
 [5 , 6 , 7 , 8 ],
 [9 , 10, 11, 12]])

>>> tril1 = paddle.tril(data)
>>> print(tril1)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 0 , 0 , 0 ],
 [5 , 6 , 0 , 0 ],
 [9 , 10, 11, 0 ]])

>>> # example 2, positive diagonal value
>>> tril2 = paddle.tril(data, diagonal=2)
>>> print(tril2)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 , 0 ],
 [5 , 6 , 7 , 8 ],
 [9 , 10, 11, 12]])

>>> # example 3, negative diagonal value
>>> tril3 = paddle.tril(data, diagonal=-1)
>>> print(tril3)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0 , 0 , 0 , 0 ],
 [5 , 0 , 0 , 0 ],
 [9 , 10, 0 , 0 ]])

tril_ ( diagonal: int = 0, name: str | None = None ) → paddle.Tensor | None [source] tril_¶: Inplace version of tril API, the output Tensor will be inplaced with input x. Please refer to tril.

triu ( diagonal: int = 0, name: Optional[str] = None ) → Tensor [source] triu¶

Return the upper triangular part of a matrix (2-D tensor) or batch of matrices x, the other elements of the result tensor are set to 0. The upper triangular part of the matrix is defined as the elements on and above the diagonal.

Parameters

x (Tensor) – The input x which is a Tensor. Support data types: float64, float32, int32, int64, complex64, complex128.
diagonal (int, optional) – The diagonal to consider, default value is 0. If diagonal = 0, all elements on and above the main diagonal are retained. A positive value excludes just as many diagonals above the main diagonal, and similarly a negative value includes just as many diagonals below the main diagonal. The main diagonal are the set of indices $\{(i, i)\}$ for $i \in [0, \min\{d_{1}, d_{2}\} - 1]$ where $d_{1}, d_{2}$ are the dimensions of the matrix.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Results of upper triangular operation by the specified diagonal of input tensor x, it’s data type is the same as x’s Tensor.

Return type

Tensor

Examples

>>> import paddle

>>> x = paddle.arange(1, 13, dtype="int64").reshape([3,-1])
>>> print(x)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 , 4 ],
 [5 , 6 , 7 , 8 ],
 [9 , 10, 11, 12]])

>>> # example 1, default diagonal
>>> triu1 = paddle.tensor.triu(x)
>>> print(triu1)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 , 4 ],
 [0 , 6 , 7 , 8 ],
 [0 , 0 , 11, 12]])

>>> # example 2, positive diagonal value
>>> triu2 = paddle.tensor.triu(x, diagonal=2)
>>> print(triu2)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[0, 0, 3, 4],
 [0, 0, 0, 8],
 [0, 0, 0, 0]])

>>> # example 3, negative diagonal value
>>> triu3 = paddle.tensor.triu(x, diagonal=-1)
>>> print(triu3)
Tensor(shape=[3, 4], dtype=int64, place=Place(cpu), stop_gradient=True,
[[1 , 2 , 3 , 4 ],
 [5 , 6 , 7 , 8 ],
 [0 , 10, 11, 12]])

triu_ ( diagonal: int = 0, name: str | None = None ) → paddle.Tensor | None [source] triu_¶: Inplace version of triu API, the output Tensor will be inplaced with input x. Please refer to triu.

trunc ( name: str | None = None ) → Tensor [source] trunc¶

This API is used to returns a new tensor with the truncated integer values of input.

Parameters

input (Tensor) – The input tensor, it’s data type should be int32, int64, float32, float64.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

The output Tensor of trunc.

Return type

Tensor

Examples

>>> import paddle

>>> input = paddle.to_tensor([[0.1, 1.5], [-0.2, -2.4]], 'float32')
>>> output = paddle.trunc(input)
>>> output
Tensor(shape=[2, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[ 0.,  1.],
 [-0., -2.]])

trunc_ ( name: str | None = None ) → Tensor [source] trunc_¶: Inplace version of trunc API, the output Tensor will be inplaced with input x. Please refer to trunc.

type

Tensor’s type.

Returns: Tensor’s type.
Return type: VarType

Examples

>>> import paddle

>>> x = paddle.to_tensor(1.)
>>> print(x.type)
VarType.DENSE_TENSOR

unbind ( axis: int = 0 ) → list[Tensor] [source] unbind¶

Removes a tensor dimension, then split the input tensor into multiple sub-Tensors.

Parameters

input (Tensor) – The input variable which is an N-D Tensor, data type being bool, float16, float32, float64, int32, int64, complex64 or complex128.
axis (int, optional) – A 0-D Tensor with shape [] and type is int32|int64. The dimension along which to unbind. If $axis < 0$, the dimension to unbind along is $rank(input) + axis$. Default is 0.

Returns

list(Tensor), The list of segmented Tensor variables.

Examples

>>> import paddle

>>> # input is a Tensor which shape is [3, 4, 5]
>>> input = paddle.rand([3, 4, 5])

>>> [x0, x1, x2] = paddle.unbind(input, axis=0)
>>> # x0.shape [4, 5]
>>> # x1.shape [4, 5]
>>> # x2.shape [4, 5]

>>> [x0, x1, x2, x3] = paddle.unbind(input, axis=1)
>>> # x0.shape [3, 5]
>>> # x1.shape [3, 5]
>>> # x2.shape [3, 5]
>>> # x3.shape [3, 5]

unflatten ( axis: int, shape: ShapeLike, name: str | None = None ) → Tensor [source] unflatten¶

Expand a certain dimension of the input x Tensor into a desired shape.

The figure below shows the shape of a [2, 6] Tensor after applying unflatten(X, axis=1, shape=(2, 3)), with data ranging from 0 to 11 in sequence.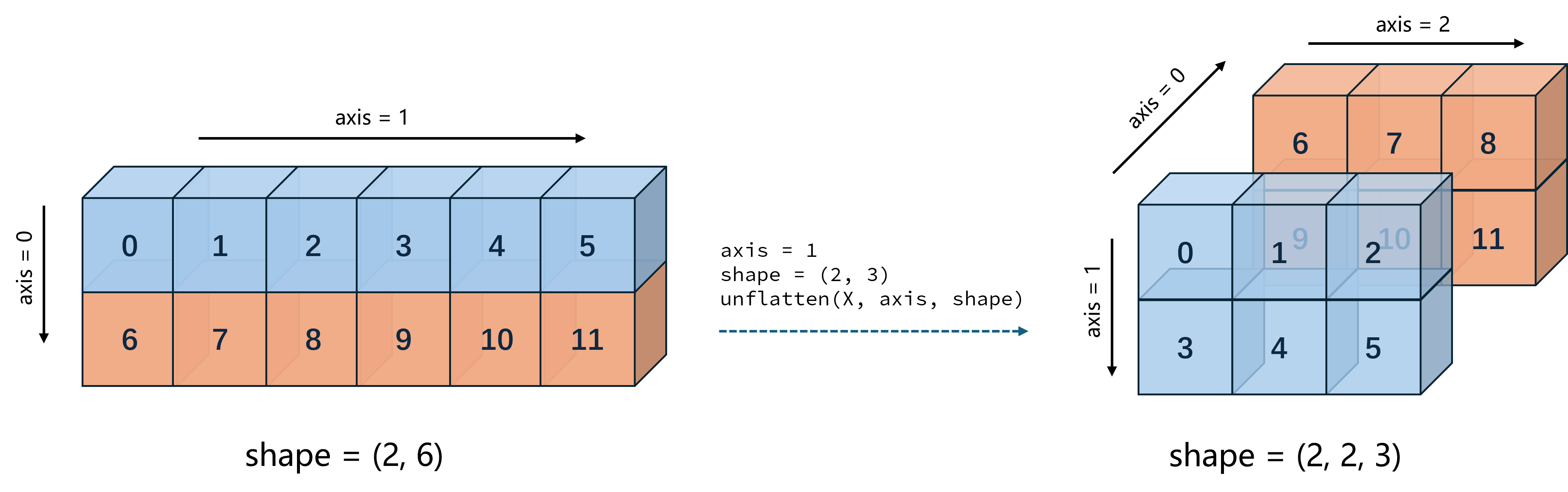

Parameters

x (Tensor) – An N-D Tensor. The data type is float16, float32, float64, int16, int32, int64, bool, uint16.
axis (int) – axis to be unflattened, specified as an index into x.shape.
shape (list|tuple|Tensor) – Unflatten shape on the specified axis. At most one dimension of the target shape can be -1. If the input shape does not contain -1 , the product of all elements in shape should be equal to x.shape[axis]. The data type is int . If shape is a list or tuple, the elements of it should be integers or Tensors with shape []. If shape is an Tensor, it should be an 1-D Tensor.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, return the unflatten tensor of x.

Examples

>>> import paddle

>>> x = paddle.randn(shape=[4, 6, 8])
>>> shape = [2, 3]
>>> axis = 1
>>> res = paddle.unflatten(x, axis, shape)
>>> print(res.shape)
[4, 2, 3, 8]

>>> x = paddle.randn(shape=[4, 6, 8])
>>> shape = (-1, 2)
>>> axis = -1
>>> res = paddle.unflatten(x, axis, shape)
>>> print(res.shape)
[4, 6, 4, 2]

>>> x = paddle.randn(shape=[4, 6, 8])
>>> shape = paddle.to_tensor([2, 2])
>>> axis = 0
>>> res = paddle.unflatten(x, axis, shape)
>>> print(res.shape)
[2, 2, 6, 8]

unfold ( axis: int, size: int, step: int, name: str | None = None ) → Tensor [source] unfold¶

View x with specified shape, stride and offset, which contains all slices of size from x in the dimension axis.

Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode.

Parameters

x (Tensor) – An N-D Tensor. The data type is float32, float64, int32, int64 or bool
axis (int) – The axis along which the input is unfolded.
size (int) – The size of each slice that is unfolded.
step (int) – The step between each slice.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A unfold Tensor with the same data type as x.

Examples

>>> import paddle
>>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True})

>>> x = paddle.arange(9, dtype="float64")

>>> out = paddle.unfold(x, 0, 2, 4)
>>> print(out)
Tensor(shape=[2, 2], dtype=float64, place=Place(cpu), stop_gradient=True,
[[0., 1.],
 [4., 5.]])

uniform_ ( min: float = -1.0, max: float = 1.0, seed: int = 0, name: str | None = None ) → Tensor uniform_¶

This is the inplace version of OP uniform, which returns a Tensor filled with random values sampled from a uniform distribution. The output Tensor will be inplaced with input x. Please refer to uniform.

Parameters

x (Tensor) – The input tensor to be filled with random values.
min (float|int, optional) – The lower bound on the range of random values to generate, min is included in the range. Default is -1.0.
max (float|int, optional) – The upper bound on the range of random values to generate, max is excluded in the range. Default is 1.0.
seed (int, optional) – Random seed used for generating samples. If seed is 0, it will use the seed of the global default generator (which can be set by paddle.seed). Note that if seed is not 0, this operator will always generate the same random numbers every time. Default is 0.
name (str|None, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name.

Returns

Tensor, The input tensor x filled with random values sampled from a uniform distribution in the range [min, max).

Examples

>>> import paddle

>>> # example:
>>> x = paddle.ones(shape=[3, 4])
>>> x.uniform_()
>>> 
Tensor(shape=[3, 4], dtype=float32, place=Place(cpu), stop_gradient=True,
[[-0.50484276,  0.49580324,  0.33357990, -0.93924278],
 [ 0.39779735,  0.87677515, -0.24377221,  0.06212139],
 [-0.92499518, -0.96244860,  0.79210341, -0.78228098]])
>>> 

unique ( return_index=False, return_inverse=False, return_counts=False, axis=None, dtype='int64', name=None ) [source] unique¶

Returns the unique elements of x in ascending order.

Parameters

x (Tensor) – The input tensor, it’s data type should be float32, float64, int32, int64.
return_index (bool, optional) – If True, also return the indices of the input tensor that result in the unique Tensor.
return_inverse (bool, optional) – If True, also return the indices for where elements in the original input ended up in the returned unique tensor.
return_counts (bool, optional) – If True, also return the counts for each unique element.
axis (int, optional) – The axis to apply unique. If None, the input will be flattened. Default: None.
dtype (np.dtype|str, optional) – The date type of indices or inverse tensor: int32 or int64. Default: int64.
name (str|None, optional) – Name for the operation. For more information, please refer to Name. Default: None.

Returns

tuple (out, indices, inverse, counts). out is the unique tensor for x. indices is: provided only if return_index is True. inverse is provided only if return_inverse is True. counts is provided only if return_counts is True.

Examples

>>> import paddle

>>> x = paddle.to_tensor([2, 3, 3, 1, 5, 3])
>>> unique = paddle.unique(x)
>>> print(unique)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 2, 3, 5])

>>> _, indices, inverse, counts = paddle.unique(x, return_index=True, return_inverse=True, return_counts=True)
>>> print(indices)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[3, 0, 1, 4])
>>> print(inverse)
Tensor(shape=[6], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 2, 2, 0, 3, 2])
>>> print(counts)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 1, 3, 1])

>>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1], [2, 1, 3]])
>>> unique = paddle.unique(x)
>>> print(unique)
Tensor(shape=[4], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 1, 2, 3])

>>> unique = paddle.unique(x, axis=0)
>>> print(unique)
Tensor(shape=[2, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[2, 1, 3],
 [3, 0, 1]])

unique_consecutive ( return_inverse: bool = False, return_counts: bool = False, axis: int | None = None, dtype: DTypeLike = 'int64', name: str | None = None ) → tuple[Tensor, Tensor, Tensor] [source] unique_consecutive¶

Eliminates all but the first element from every consecutive group of equivalent elements.

Note

This function is different from unique in the sense that this function only eliminates consecutive duplicate values. This semantics is similar to unique in C++.

Parameters

x (Tensor) – the input tensor, it’s data type should be float32, float64, int32, int64.
return_inverse (bool, optional) – If True, also return the indices for where elements in the original input ended up in the returned unique consecutive tensor. Default is False.
return_counts (bool, optional) – If True, also return the counts for each unique consecutive element. Default is False.
axis (int, optional) – The axis to apply unique consecutive. If None, the input will be flattened. Default is None.
dtype (np.dtype|str, optional) – The data type inverse tensor: int32 or int64. Default: int64.
name (str|None, optional) – Name for the operation. For more information, please refer to Name. Default is None.

Returns

out (Tensor), the unique consecutive tensor for x.
inverse (Tensor), the element of the input tensor corresponds to

the index of the elements in the unique consecutive tensor for x. inverse is provided only if return_inverse is True.
counts (Tensor), the counts of the every unique consecutive element in the input tensor.

counts is provided only if return_counts is True.

Examples

>>> import paddle

>>> x = paddle.to_tensor([1, 1, 2, 2, 3, 1, 1, 2])
>>> output = paddle.unique_consecutive(x) #
>>> print(output)
Tensor(shape=[5], dtype=int64, place=Place(cpu), stop_gradient=True,
[1, 2, 3, 1, 2])

>>> _, inverse, counts = paddle.unique_consecutive(x, return_inverse=True, return_counts=True)
>>> print(inverse)
Tensor(shape=[8], dtype=int64, place=Place(cpu), stop_gradient=True,
[0, 0, 1, 1, 2, 3, 3, 4])
>>> print(counts)
Tensor(shape=[5], dtype=int64, place=Place(cpu), stop_gradient=True,
 [2, 2, 1, 2, 1])

>>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1], [2, 1, 3], [2, 1, 3]])
>>> output = paddle.unique_consecutive(x, axis=0) #
>>> print(output)
Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[2, 1, 3],
 [3, 0, 1],
 [2, 1, 3]])

>>> x = paddle.to_tensor([[2, 1, 3], [3, 0, 1], [2, 1, 3], [2, 1, 3]])
>>> output = paddle.unique_consecutive(x, axis=0) #
>>> print(output)
Tensor(shape=[3, 3], dtype=int64, place=Place(cpu), stop_gradient=True,
[[2, 1, 3],
 [3, 0, 1],
 [2, 1, 3]])

unsqueeze ( axis: int | Sequence[Tensor | int] | Tensor, name: str | None = None ) → Tensor [source] unsqueeze¶

Insert single-dimensional entries to the shape of input Tensor x. Takes one required argument axis, a dimension or list of dimensions that will be inserted. Dimension indices in axis are as seen in the output tensor.

Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode. If you want to use the Tensor copy version, please use Tensor.clone like unsqueeze_clone_x = x.unsqueeze(-1).clone().

Parameters

x (Tensor) – The input Tensor to be unsqueezed. Supported data type: bfloat16, float16, float32, float64, bool, int8, int32, int64.
axis (int|list|tuple|Tensor) – Indicates the dimensions to be inserted. The data type is int32 . If axis is a list or tuple, each element of it should be integer or 0-D Tensor with shape []. If axis is a Tensor, it should be an 1-D Tensor . If axis is negative, axis = axis + ndim(x) + 1.
name (str|None, optional) – Name for this layer. Please refer to Name, Default None.

Returns

Tensor, Unsqueezed Tensor with the same data type as input Tensor.

Examples

>>> import paddle

>>> x = paddle.rand([5, 10])
>>> print(x.shape)
[5, 10]

>>> out1 = paddle.unsqueeze(x, axis=0)
>>> print(out1.shape)
[1, 5, 10]

>>> out2 = paddle.unsqueeze(x, axis=[0, 2])
>>> print(out2.shape)
[1, 5, 1, 10]

>>> axis = paddle.to_tensor([0, 1, 2])
>>> out3 = paddle.unsqueeze(x, axis=axis)
>>> print(out3.shape)
[1, 1, 1, 5, 10]

>>> # out1, out2, out3 share data with x in dygraph mode
>>> x[0, 0] = 10.
>>> print(out1[0, 0, 0])
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
10.)
>>> print(out2[0, 0, 0, 0])
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
10.)
>>> print(out3[0, 0, 0, 0, 0])
Tensor(shape=[], dtype=float32, place=Place(cpu), stop_gradient=True,
10.)

unsqueeze_ ( axis: int | Sequence[int] | Tensor, name: str | None = None ) → Tensor [source] unsqueeze_¶: Inplace version of unsqueeze API, the output Tensor will be inplaced with input x. Please refer to api_paddle_tensor_unsqueeze.

unstack ( axis: int = 0, num: int | None = None ) → Tensor [source] unstack¶

This layer unstacks input Tensor x into several Tensors along axis.

If axis < 0, it would be replaced with axis+rank(x). If num is None, it would be inferred from x.shape[axis], and if x.shape[axis] <= 0 or is unknown, ValueError is raised.

Parameters

x (Tensor) – Input Tensor. It is a N-D Tensors of data types float32, float64, int32, int64, complex64, complex128.
axis (int, optional) – The axis along which the input is unstacked.
num (int|None, optional) – The number of output variables.

Returns

list(Tensor), The unstacked Tensors list. The list elements are N-D Tensors of data types float32, float64, int32, int64, complex64, complex128.

Examples

>>> import paddle
>>> x = paddle.ones(name='x', shape=[2, 3, 5], dtype='float32')  # create a tensor with shape=[2, 3, 5]
>>> y = paddle.unstack(x, axis=1)  # unstack with second axis, which results 3 tensors with shape=[2, 5]

values ( ) → Tensor values¶

Notes:: This API is ONLY available in Dygraph mode

Get the values of current SparseTensor(COO or CSR).

Returns: A DenseTensor
Return type: Tensor

Examples

>>> import paddle
>>> indices = [[0, 0, 1, 2, 2], [1, 3, 2, 0, 1]]
>>> values = [1, 2, 3, 4, 5]
>>> dense_shape = [3, 4]
>>> sparse_x = paddle.sparse.sparse_coo_tensor(paddle.to_tensor(indices, dtype='int32'), paddle.to_tensor(values, dtype='float32'), shape=dense_shape)
>>> print(sparse_x.values())
Tensor(shape=[5], dtype=float32, place=Place(cpu), stop_gradient=True,
[1., 2., 3., 4., 5.])

vander ( n: int | None = None, increasing: bool = False, name: str | None = None ) → Tensor [source] vander¶

Generate a Vandermonde matrix.

The columns of the output matrix are powers of the input vector. Order of the powers is determined by the increasing Boolean parameter. Specifically, when the increment is “false”, the ith output column is a step-up in the order of the elements of the input vector to the N - i - 1 power. Such a matrix with a geometric progression in each row is named after Alexandre-Theophile Vandermonde.

Parameters

x (Tensor) – The input tensor, it must be 1-D Tensor, and it’s data type should be [‘complex64’, ‘complex128’, ‘float32’, ‘float64’, ‘int32’, ‘int64’].
n (int|None) – Number of columns in the output. If n is not specified, a square array is returned (n = len(x)).
increasing (bool) – Order of the powers of the columns. If True, the powers increase from left to right, if False (the default) they are reversed.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, A vandermonde matrix with shape (len(x), N). If increasing is False, the first column is $x^{(N-1)}$, the second $x^{(N-2)}$ and so forth. If increasing is True, the columns are $x^0$, $x^1$, …, $x^{(N-1)}$.

Examples

>>> import paddle
>>> x = paddle.to_tensor([1., 2., 3.], dtype="float32")
>>> out = paddle.vander(x)
>>> out
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 1., 1.],
 [4., 2., 1.],
 [9., 3., 1.]])
>>> out1 = paddle.vander(x,2)
>>> out1
Tensor(shape=[3, 2], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 1.],
 [2., 1.],
 [3., 1.]])
>>> out2 = paddle.vander(x, increasing = True)
>>> out2
Tensor(shape=[3, 3], dtype=float32, place=Place(cpu), stop_gradient=True,
[[1., 1., 1.],
 [1., 2., 4.],
 [1., 3., 9.]])
>>> real = paddle.to_tensor([2., 4.])
>>> imag = paddle.to_tensor([1., 3.])
>>> complex = paddle.complex(real, imag)
>>> out3 = paddle.vander(complex)
>>> out3
Tensor(shape=[2, 2], dtype=complex64, place=Place(cpu), stop_gradient=True,
[[(2+1j), (1+0j)],
 [(4+3j), (1+0j)]])

var ( axis: int | Sequence[int] | None = None, unbiased: bool = True, keepdim: bool = False, name: str | None = None ) → Tensor [source] var¶

Computes the variance of x along axis .

Parameters

x (Tensor) – The input Tensor with data type float16, float32, float64.
axis (int|list|tuple|None, optional) –
The axis along which to perform variance calculations. axis should be int, list(int) or tuple(int).
- If axis is a list/tuple of dimension(s), variance is calculated along all element(s) of axis . axis or element(s) of axis should be in range [-D, D), where D is the dimensions of x .
- If axis or element(s) of axis is less than 0, it works the same way as $axis + D$ .
- If axis is None, variance is calculated over all elements of x. Default is None.
unbiased (bool, optional) – Whether to use the unbiased estimation. If unbiased is True, the divisor used in the computation is $N - 1$, where $N$ represents the number of elements along axis , otherwise the divisor is $N$. Default is True.
keep_dim (bool, optional) – Whether to reserve the reduced dimension in the output Tensor. The result tensor will have one fewer dimension than the input unless keep_dim is true. Default is False.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, results of variance along axis of x, with the same data type as x.

Examples

>>> import paddle

>>> x = paddle.to_tensor([[1.0, 2.0, 3.0], [1.0, 4.0, 5.0]])
>>> out1 = paddle.var(x)
>>> print(out1.numpy())
2.6666667
>>> out2 = paddle.var(x, axis=1)
>>> print(out2.numpy())
[1.         4.3333335]

view ( shape_or_dtype: Sequence[int] | DTypeLike, name: str | None = None ) → Tensor [source] view¶

View x with specified shape or dtype.

Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode.

Parameters

x (Tensor) – An N-D Tensor. The data type is float32, float64, int32, int64 or bool
shape_or_dtype (list|tuple|np.dtype|str|VarType) – Define the target shape or dtype. If list or tuple, shape_or_dtype represents shape, each element of it should be integer. If np.dtype or str or VarType, shape_or_dtype represents dtype, it can be bool, float16, float32, float64, int8, int32, int64, uint8.
name (str, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A viewed Tensor with the same data as x.

Examples

>>> import paddle
>>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True})

>>> x = paddle.rand([2, 4, 6], dtype="float32")

>>> out = paddle.view(x, [8, 6])
>>> print(out.shape)
[8, 6]

>>> import paddle
>>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True})

>>> x = paddle.rand([2, 4, 6], dtype="float32")

>>> out = paddle.view(x, "uint8")
>>> print(out.shape)
[2, 4, 24]

>>> import paddle
>>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True})

>>> x = paddle.rand([2, 4, 6], dtype="float32")

>>> out = paddle.view(x, [8, -1])
>>> print(out.shape)
[8, 6]

>>> import paddle
>>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True})

>>> x = paddle.rand([2, 4, 6], dtype="float32")

>>> out = paddle.view(x, paddle.uint8)
>>> print(out.shape)
[2, 4, 24]

view_as ( other: Tensor, name: str | None = None ) → Tensor [source] view_as¶

View x with other’s shape.

Note that the output Tensor will share data with origin Tensor and doesn’t have a Tensor copy in dygraph mode.

The following figure shows a view_as operation - a three-dimensional tensor with a shape of [2, 4, 6] is transformed into a two-dimensional tensor with a shape of [8, 6] through the view_as operation. We can clearly see the corresponding relationship between the elements before and after the transformation.

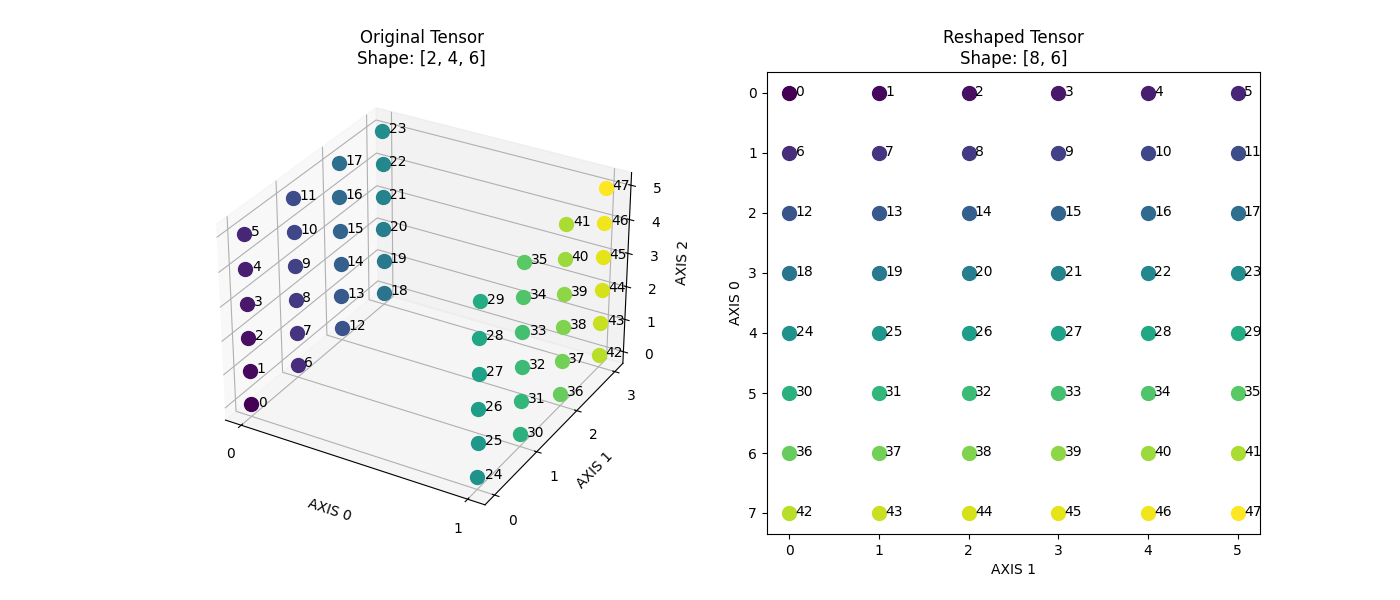
Parameters

x (Tensor) – An N-D Tensor. The data type is float32, float64, int32, int64 or bool
other (Tensor) – The result tensor has the same size as other.
name (str|None, optional) – Name for the operation (optional, default is None). For more information, please refer to Name.

Returns

Tensor, A viewed Tensor with the same shape as other.

Examples

>>> import paddle
>>> paddle.base.set_flags({"FLAGS_use_stride_kernel": True})

>>> x = paddle.rand([2, 4, 6], dtype="float32")
>>> y = paddle.rand([8, 6], dtype="float32")

>>> out = paddle.view_as(x, y)
>>> print(out.shape)
[8, 6]

vsplit ( num_or_indices: int | Sequence[int], name: str | None = None ) → list[Tensor] [source] vsplit¶

vsplit Full name Vertical Split, splits the input Tensor into multiple sub-Tensors along the vertical axis, which is equivalent to paddle.tensor_split with axis=0.

When the number of Tensor dimensions is equal to 2:

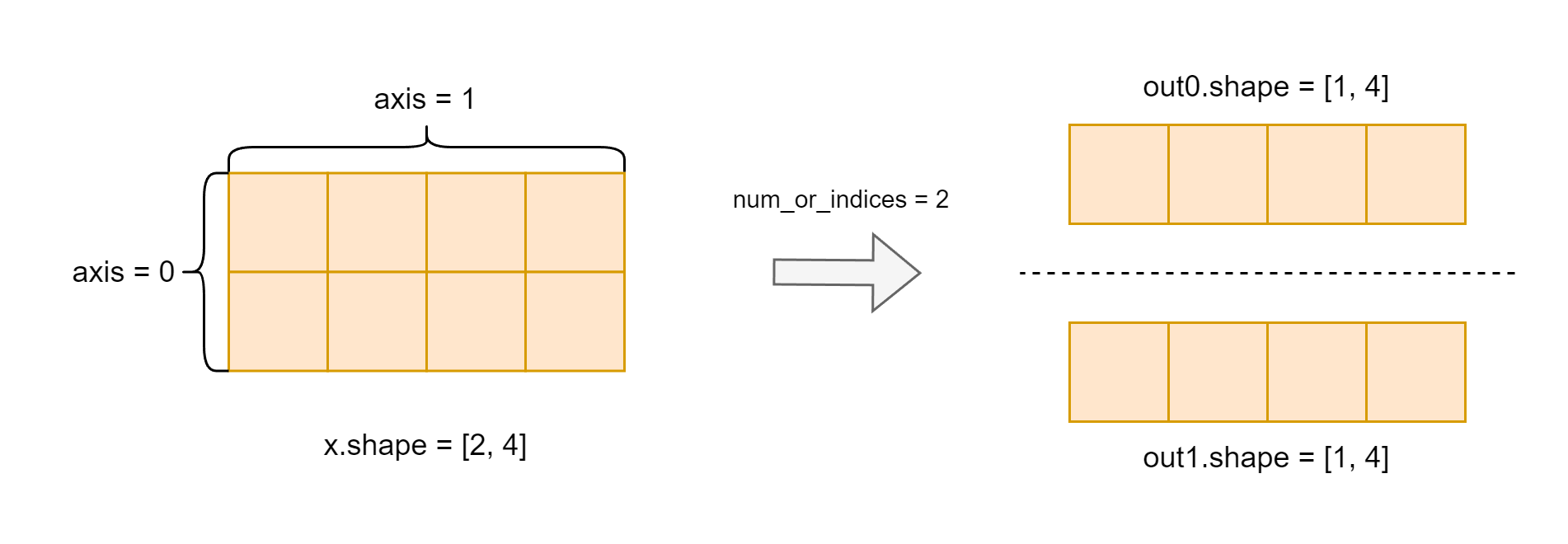
https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/vsplit/vsplit-1.png

When the number of Tensor dimensions is greater than 2:

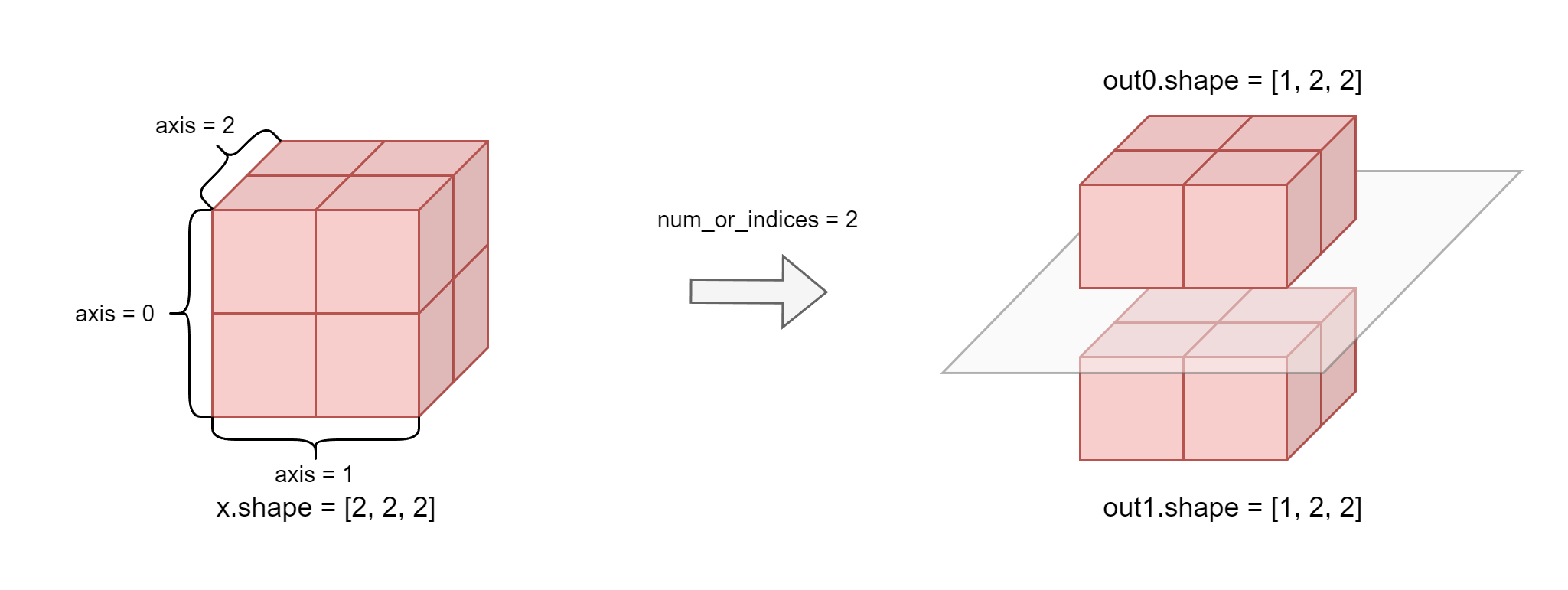
https://githubraw.cdn.bcebos.com/PaddlePaddle/docs/develop/docs/images/api_legend/vsplit/vsplit-2.png

Note

Make sure that the number of Tensor dimensions transformed using paddle.vsplit must be not less than 2.

Parameters

x (Tensor) – A Tensor whose dimension must be greater than 1. The data type is bool, bfloat16, float16, float32, float64, uint8, int32 or int64.
num_or_indices (int|list|tuple) – If num_or_indices is an int n, x is split into n sections. If num_or_indices is a list or tuple of integer indices, x is split at each of the indices.
name (str, optional) – The default value is None. Normally there is no need for user to set this property. For more information, please refer to Name .

Returns

list[Tensor], The list of segmented Tensors.

Examples

>>> import paddle

>>> # x is a Tensor of shape [8, 6, 7]
>>> x = paddle.rand([8, 6, 7])
>>> out0, out1 = paddle.vsplit(x, num_or_indices=2)
>>> print(out0.shape)
[4, 6, 7]
>>> print(out1.shape)
[4, 6, 7]

>>> out0, out1, out2 = paddle.vsplit(x, num_or_indices=[1, 4])
>>> print(out0.shape)
[1, 6, 7]
>>> print(out1.shape)
[3, 6, 7]
>>> print(out2.shape)
[4, 6, 7]

Return a Tensor of elements selected from either x or y according to corresponding elements of condition. Concretely,

\[\begin{split}out_i = \begin{cases} x_i, & \text{if} \ condition_i \ \text{is} \ True \\ y_i, & \text{if} \ condition_i \ \text{is} \ False \\ \end{cases}.\end{split}\]

Notes

numpy.where(condition) is identical to paddle.nonzero(condition, as_tuple=True), please refer to nonzero.

Parameters

condition (Tensor) – The condition to choose x or y. When True (nonzero), yield x, otherwise yield y, must have a dtype of bool if used as mask.
x (Tensor|scalar|None, optional) – A Tensor or scalar to choose when the condition is True with data type of bfloat16, float16, float32, float64, int32 or int64. Either both or neither of x and y should be given.
y (Tensor|scalar|None, optional) – A Tensor or scalar to choose when the condition is False with data type of bfloat16, float16, float32, float64, int32 or int64. Either both or neither of x and y should be given.
name (str|None, optional) – For details, please refer to Name. Generally, no setting is required. Default: None.

Returns

Tensor, A Tensor with the same shape as condition and same data type as x and y.

Examples

>>> import paddle

>>> x = paddle.to_tensor([0.9383, 0.1983, 3.2, 1.2])
>>> y = paddle.to_tensor([1.0, 1.0, 1.0, 1.0])

>>> out = paddle.where(x>1, x, y)
>>> print(out)
Tensor(shape=[4], dtype=float32, place=Place(cpu), stop_gradient=True,
[1.        , 1.        , 3.20000005, 1.20000005])

>>> out = paddle.where(x>1)
>>> print(out)
(Tensor(shape=[2, 1], dtype=int64, place=Place(cpu), stop_gradient=True,
[[2],
 [3]]),)

where_ ( x: Tensor | float | None = None, y: Tensor | float | None = None, name: str | None = None ) → Tensor [source] where_¶: Inplace version of where API, the output Tensor will be inplaced with input x. Please refer to where.

zero_ ( ) → Tensor zero_¶

Notes:: This API is ONLY available in Dygraph mode

This function fill the Tensor with zero inplace.

Parameters: x (Tensor) – x is the Tensor we want to filled with zero inplace
Returns: x (Tensor), Tensor x filled with zero inplace

Examples

>>> import paddle

>>> tensor = paddle.to_tensor([0, 1, 2, 3, 4])

>>> tensor.zero_()
>>> print(tensor.tolist())
[0, 0, 0, 0, 0]

Tensor

abs¶

abs_¶

acos¶

acos_¶

acosh¶

acosh_¶

add¶

add_¶

add_n¶

addmm¶

addmm_¶

all¶

allclose¶

amax¶

amin¶

angle¶

any¶

apply¶

apply_¶

argmax¶

argmin¶

argsort¶

as_complex¶

as_real¶

as_strided¶

asin¶

asin_¶

asinh¶

asinh_¶

astype¶

atan¶

atan2¶

atan_¶

atanh¶

atanh_¶

atleast_1d¶

atleast_2d¶

atleast_3d¶

backward¶

baddbmm¶

baddbmm_¶

bernoulli_¶

bincount¶

bitwise_and¶

bitwise_and_¶

bitwise_invert¶

bitwise_invert_¶

bitwise_left_shift¶

bitwise_left_shift_¶

bitwise_not¶

bitwise_not_¶

bitwise_or¶

bitwise_or_¶

bitwise_right_shift¶

bitwise_right_shift_¶

bitwise_xor¶

bitwise_xor_¶

block_diag¶

bmm¶

broadcast_shape¶

broadcast_tensors¶

broadcast_to¶

bucketize¶

cast¶

cast_¶

cauchy_¶

cdist¶

ceil¶

ceil_¶

cholesky¶

cholesky_inverse¶

cholesky_solve¶

chunk¶

clear_grad¶

clear_gradient¶

clip¶

clip_¶

clone¶

coalesce¶