自动混合精度¶

传统上，深度学习训练通常使用 32 比特双精度浮点数FP32 作为参数、梯度和中间 Activation 等的数据存储格式。使用FP32作为数据存储格式，每个数据需要 4 个字节的存储空间。为了节约显存消耗，业界提出使用 16 比特单精度浮点数FP16作为数据存储格式。使用FP16作为数据存储格式，每个数据仅需要 2 个字节的存储空间，相比于FP32可以节省一半的存储空间。除了降低显存消耗，FP16格式下，计算速度通常也更快，因此可以加速训练。

单精度浮点训练可以带来以下好处：

减少对 GPU 显存的需求，或者在 GPU 显存保持不变的情况下，可以支持更大模型和更大的 batch size；
降低显存读写的带宽压力；
加速 GPU 数学运算速度 (需要 GPU 支持[1])；按照 NVIDA 数据，GPU 上FP16计算吞吐量是FP32的 2~8 倍[2]。

一、原理介绍¶

我们首先介绍半精度（FP16）浮点数的表示，如下图所示。半精度浮点数是一种相对较新的浮点类型，在计算机中使用 2 字节（16 比特）存储。在 IEEE 754-2008 标准中，它亦被称作 binary16。与计算中常用的单精度（FP32）和双精度（FP64）浮点类型相比，因为 FP16 表示范围和表示精度更低，因此 FP16 更适于在精度要求不高的场景中使用。

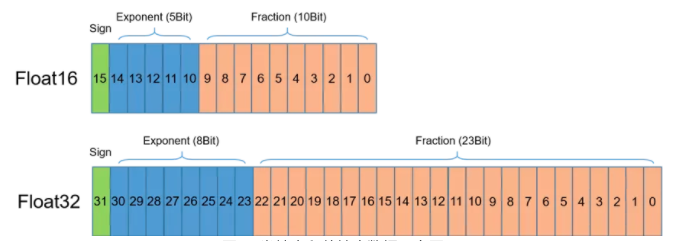
在使用相同的超参数下，混合精度训练使用半精度浮点（FP16）和单精度（FP32）浮点即可达到与使用纯单精度训练相同的准确率，并可加速模型的训练速度。这主要得益于英伟达推出的 Volta 及 Turing 架构 GPU 在使用 FP16 计算时具有如下特点：

FP16 可降低一半的内存带宽和存储需求，这使得在相同的硬件条件下研究人员可使用更大更复杂的模型以及更大的 batch size 大小。
FP16 可以充分利用英伟达 Volta 及 Turing 架构 GPU 提供的 Tensor Cores 技术。在相同的 GPU 硬件上，Tensor Cores 的 FP16 计算吞吐量是 FP32 的 8 倍。

使用自动混合精度训练时，主要训练过程如下：模型参数使用单精度浮点格式存储，在实际计算时，模型参数从单精度浮点数转换为半精度浮点数参与前向计算，并得到半精度浮点数表示中间状态和模型的 loss 值，然后使用半精度浮点数计算梯度，并将参数对应的梯度转换为单精度浮点数格式后，更新模型参数。计算过程如下图所示。

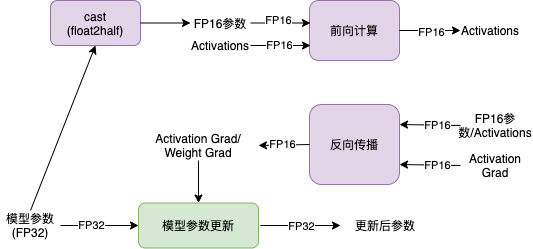
如前所述，通常半精度浮点数的表示范围远小于单精度浮点数的表示范围，在深度学习领域，参数、中间状态和梯度的值通常很小，因此以半精度浮点数参与计算时容易出现数值下溢，即接近零的值下溢为零值。为了避免这个问题，通常采用loss scaling机制。具体地讲，对 loss 乘以一个称为loss_scaling的值，根据链式法则，在反向传播过程中，梯度也等价于相应的乘以了loss_scaling的值，因此在参数更新时需要将梯度值相应地除以loss_scaling的值。

然而，在模型训练过程中，选择合适的loss_scaling的值是个较大的挑战。因此，需要采用一种称为动态 loss scaling的机制。用户只需要为loss_scaling设置一个初始值：init_loss_scaling。在训练过程中，会检查梯度值是否出现 nan 或 inf 值，当连续incr_every_n_steps次迭代均未出现 nan 和 inf 值时，将init_loss_scaling的值乘以一个因子：incr_ratio；当连续decr_every_n_steps次迭代均出现 nan 和 inf 值时，将init_loss_scaling的值除以一个因子：decr_ratio。

同时，我们知道某些算子不适合采用半精度浮点数参与计算，因为这类算子采用半精度浮点数进行计算容易出现 nan 或者 inf 值。为了解决这个问题，通常采用黑名单和白名单机制。其中，黑名单中放置不宜采用半精度浮点数进行计算的算子，白名单中放置适合采用半精度浮点数进行计算的算子。

飞桨中，我们引入自动混合精度(Auto Mixed Precision, AMP)，混合使用FP32和FP16，在保持训练精度的同时，进一步提升训练的速度。实现了 自动维护 FP32 、FP16 参数副本,动态 loss scaling, op 黑白名单 等策略来避免因FP16动态范围较小而带来的模型最终精度损失。Fleet 作为飞桨通用的分布式训练 API 提供了简单易用的接口, 用户只需要添加几行代码就可将自动混合精度应用到原有的分布式训练中进一步提升训练速度。

二、动态图操作实践¶

使用飞桨框架提供的 API：paddle.amp.auto_cast和paddle.amp.GradScaler能够实现动态图的自动混合精度训练，即在相关 OP 的计算中，自动选择 FP16 或 FP32 格式计算。开启 AMP 模式后，使用 FP16 与 FP32 进行计算的 OP 列表可以参见 paddle.amp 。

2.1 具体示例¶

下面来看一个具体的例子，来了解如果使用飞桨框架实现动态图自动混合精度训练。

首先定义辅助函数，用来计算训练时间。

           import time

# 开始时间
start_time = None

def start_timer():
   # 获取开始时间
   global start_time
   start_time = time.time()

def end_timer_and_print(msg):
   # 打印信息并输出训练时间
   end_time = time.time()
   print("\n" + msg)
   print("共计耗时 = {:.3f} sec".format(end_time - start_time))

          

接着构建一个简单的网络，用于对比使用单精度浮点数进行训练与使用自动混合精度训练的速度。该网络由三层 Linear 组成，其中前两层 Linear 后接 ReLU 激活函数。

           import paddle
import paddle.nn as nn

class SimpleNet(nn.Layer):

   def __init__(self, input_size, output_size):
      super().__init__()
      self.linear1 = nn.Linear(input_size, output_size)
      self.relu1 = nn.ReLU()
      self.linear2 = nn.Linear(input_size, output_size)
      self.relu2 = nn.ReLU()
      self.linear3 = nn.Linear(input_size, output_size)

   def forward(self, x):

      x = self.linear1(x)
      x = self.relu1(x)
      x = self.linear2(x)
      x = self.relu2(x)
      x = self.linear3(x)

      return x

          

这里为了能有效的对比自动混合精度训练在速度方面的提升，我们将 input_size 与 output_size 的值设为较大的值，为了充分利用 NVIDIA GPU 提供的 Tensor Core 能力，我们将 batch_size 设置为 8 的倍数。

           epochs = 5
input_size = 4096   # 设为较大的值
output_size = 4096  # 设为较大的值
batch_size = 512    # batch_size 为 8 的倍数
nums_batch = 50

train_data = [paddle.randn((batch_size, input_size)) for _ in range(nums_batch)]
labels = [paddle.randn((batch_size, output_size)) for _ in range(nums_batch)]

mse = paddle.nn.MSELoss()

          

下面给出单精度浮点数训练的代码：

           model = SimpleNet(input_size, output_size)  # 定义模型

optimizer = paddle.optimizer.SGD(learning_rate=0.0001, parameters=model.parameters())  # 定义优化器

start_timer() # 获取训练开始时间

for epoch in range(epochs):
   datas = zip(train_data, labels)
   for i, (data, label) in enumerate(datas):

      output = model(data)
      loss = mse(output, label)

      # 反向传播
      loss.backward()

      # 训练模型
      optimizer.step()
      optimizer.clear_grad()

print(loss)
end_timer_and_print("默认耗时:") # 获取结束时间并打印相关信息

          

下面给出程序运行的输出：

           Tensor(shape=[1], dtype=float32, place=CUDAPlace(0), stop_gradient=False,
    [1.25010288])

默认耗时:
共计耗时 = 2.943 sec

2.2 模型训练¶

下面，我们介绍在动态图中如何使用 AMP 训练模型。在飞桨框架中，使用自动混合精度训练，需要以下三个步骤：

定义 GradScaler，用于缩放 loss 比例，避免浮点数下溢，即进行loss scaling。
使用 auto_cast 创建 AMP 上下文环境，该上下文中自动会确定每个 OP 的输入数据类型（FP16 或 FP32）。
使用步骤 1 中定义的 GradScaler 完成 loss 的缩放，并用缩放后的 loss 进行反向传播，完成训练。

实现代码如下所示：

           model = SimpleNet(input_size, output_size)  # 定义模型

optimizer = paddle.optimizer.SGD(learning_rate=0.0001, parameters=model.parameters())  # 定义优化器

# Step1：定义 GradScaler，用于缩放 loss 比例，避免浮点数溢出
scaler = paddle.amp.GradScaler(init_loss_scaling=1024)

start_timer() # 获取训练开始时间

for epoch in range(epochs):
   datas = zip(train_data, labels)
   for i, (data, label) in enumerate(datas):

      # Step2：创建 AMP 上下文环境，开启自动混合精度训练
      with paddle.amp.auto_cast():
            output = model(data)
            loss = mse(output, label)

      # Step3：使用 Step1 中定义的 GradScaler 完成 loss 的缩放，用缩放后的 loss 进行反向传播
      scaled = scaler.scale(loss)
      scaled.backward()

      # 训练模型
      scaler.minimize(optimizer, scaled)
      optimizer.clear_grad()

print(loss)
end_timer_and_print("使用 AMP 模式耗时:")

          

程序的输出如下：

           Tensor(shape=[1], dtype=float32, place=CUDAPlace(0), stop_gradient=False,
    [1.23644269])

使用 AMP 模式耗时:
共计耗时 = 1.222 sec

上述例子存放在：example/amp/amp_dygraph.py。