低精度算子支持开发规范¶
一、FP16 简介及精度问题¶
1.1 FP16 简介¶
FP16 指得是半精度浮点数表示,通常意义上其表示的为 Nvidia 提供的半精度浮点数表示方案, 也被 IEEE 754-2008 方案所采纳。此方案有别于 Intel 提供的半精度表示方案 BF16, BF16 的采用直接截断尾数的方式。FP16 较 BF16 拥有更长的尾数,但阶码较短。因此 FP16 可以提供较 BF16 更好的有效位长度,而 BF16 可以提供较 FP16 更广的动态范围。
表 1-1 FP16 和 BF16 在近 1 端的精度表现
| Format | Epsilon(ε) |
|---|---|
| FP32 | 0.00000012 |
| FP16 | 0.00097656 |
| BF16 | 0.00781250 |
注:Epsilon 是各浮点表示形式下使得 1+ε >1 成立的最小浮点数值
表 1-2 FP16、FP32 与 BF16 的动态范围
| Format | Range |
|---|---|
| FP32 | 1.4E-45~3.40E38 |
| FP16 | 5.96E−8 ~ 655 |
| BF16 | 9.2E−41~3.39E38 |
1.2 FP16 格式¶
FP16 格式采用 16 位对浮点数进行表示,其中尾数位为 10 位,阶码为 5 位,符号位 1 位。
BF16 格式采用 16 位对浮点数进行表示,其中尾数位为 7 位,阶码为 8 位,符号位 1 位。
FP16 格式与 BF16、FP32 格式的比较见表 1-3。
注意阶码部分采用移码表示,偏移值为 15。即 01111(2) = 0(10)。如此方便进行 FP16 数值大小比较。
表 1-3 FP16 与 BF16、FP32 格式的对比
| Format | Bits | Exponent | Fraction |
|---|---|---|---|
| FP32 | 32 | 8 | 23 |
| FP16 | 16 | 5 | 10 |
| BF16 | 16 | 8 | 7 |
注: 表中数字均表示相应项的位数长度


1.3 FP16/BF16 的数值范围及精度¶
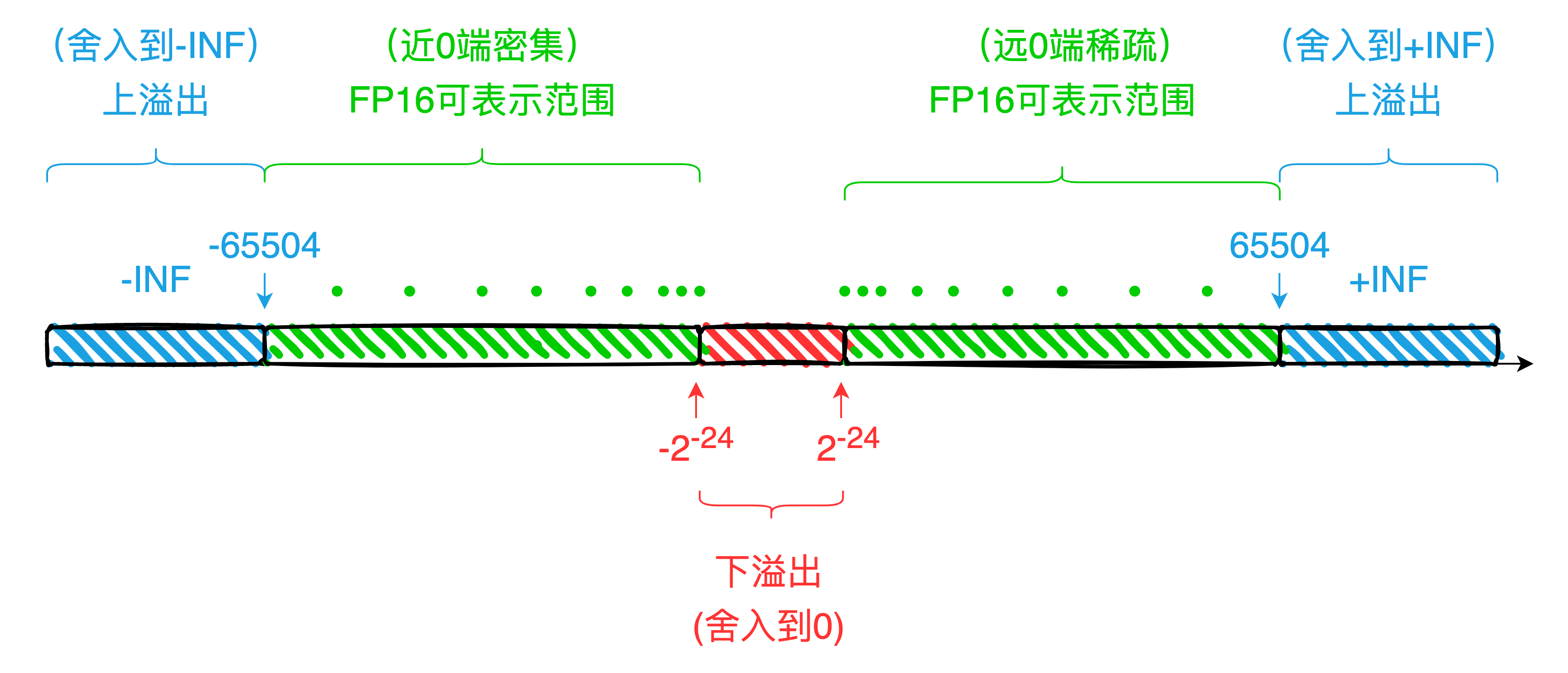
浮点数的表示方案不在本节表述之内,请自行查阅,可参考IEEE 754 相关介绍,在此不做赘述。FP16 可表示数据的最大正值为 65504,超过此数值会造成上溢出问题,舍入为+INF;最小正值约为 0.0000000596(非规格表示下),低于此数值会造成下溢出问题,舍入为+0。符号为负时以绝对值为参考,分别在满足各自情况下舍入为-INF 与-0。关于各个值的表示可见表 1-4 。
表 1-4 FP16 的各特殊值表现
| 二进制格式(符号 阶码 尾数) | 数值(十进制) | 备注 |
|---|---|---|
| X 00000 0000000000 | ±0 | |
| X 11111 0000000000 | ±INF | |
| X 11111 XXXXXXXXXX(非全 0) | Nan | |
| 0 00000 0000000001 | 0.000000059604645 | 最小正值 |
| 0 11110 0000000000 | 65504 | 最大正值 |
注:X 指 0 或 1
表 1-5 BF16 的各特殊值表现
| 二进制格式 | 数值(十进制) | 备注 |
|---|---|---|
| X 00000000 0000000 | ±0 | |
| X 11111111 0000000 | ±INF | |
| X 11111111 XXXXXXX(非全 0) | NAN | |
| 0 11111110 1111111 | $3.38953139×10^{38}$ | 最大正值 |
| 0 00000000 0000001 | 9.2 × 10−41 | 最小正值 |
注:X 指 0 或 1
通常意义上,FP16 可表示十进制下的三位有效数字格式($\log_{10}^{2^{11}}\sim3.311$) ,BF16 可表示十进制下的 2 位有效数字格式($\log_{10}^{2^{8}}\sim2.408$),但按照浮点数的格式,其表示的绝对精度(精确到哪一数位)在各个区间(本质为各个阶码下并不相同)。
1.4 FP16/BF16 在计算中的精度问题¶
1.4.1 溢出问题¶
FP16 的可表示范围较 FP32 等更小,容易触发上、下溢出问题。
关于 FP16 的上下溢出可以参考图 1-3。对于绝对值大于 65504 的数,触发上溢出会舍入到±INF;对于绝对值小于的数,触发下溢出舍入到 0,具体示例可参考表 1-6。
表 1-6 FP16 格式下数据表示示例
BF16 则因为阶码同 FP32 等长,因此并不容易出现上下溢出问题。
1.4.2 舍入问题¶
FP16 格式的浮点数最多只能表示 3 位有效数字,所以各浮点区间的固定间隔都是 $Interval=Min*2^{-10}$。
因此当 $(\frac{累加值}{加数})>2^{11}$ 时,计算结果超过了 3 位有效数字;这会造成累加值最终无法被有效表示,累加结果会被舍入到累加值本身。
数值: $1+0.0001=1.0001$
FP16: $1+0.0001=1.0001(无法表示->舍入->1)$
FP32 格式拥有 7 位有效数字的表达效果,因此当 FP32 格式向 FP16 格式转化时,也会出现精度的舍入问题。
FP32:0.1234567
FP16:0.1235
BF16 格式的浮点数,在各个区间内的固定间隔是 $Interval=Min*2^{-7}$ ,故 BF16 相较于 FP16 的精度更低,也更容易出现 FP16 中所阐述的计算舍入和转换精度丢失的问题。
二、FP16/BF16 算子开发规范及示例代码¶
对于添加算子的流程具体可参考算子添加流程,当我们向 Kernel 中添加 FP16 或 BF16 数据类型支持时,需要关注流程中如下 4 个部分。
2.1 查找对应的实现文件¶
检索对应 Kernel 的头文件
通常可以在 paddle/phi/kernels/ 目录下检索到与具体硬件无关的 Kernel 源代码文件及头文件。
检索方式。
paddle/phi/kernels/ 目录下的文件名通常形式为 Kernel 名字 + '_kernel' 。因此寻找某个具体 Kernel 的相关文件时,可以通过文件名快速查找到。如 Abs 的相关文件为 abs_kernel.h
可以利用 grep,或者 IDE 中带有的查找功能等对 Kernel 名本身进行搜索,定位具体的实现文件。
检索对应 Kernel 的 源文件 。
按照需要提供支持的硬件,在相应的目录下查找对应 Kernel 的源文件。Kernel 的 GPU 版本实现代码存放在 paddle/phi/kernels/gpu/ 目录下,CPU 版本实现代码存放在 paddle/phi/kernels/cpu/ 目录下。
FP16 数据类型一般在 GPU、XPU 上支持,可在 gpu、xpu 目录下的相关文件中添加 FP16 数据支持。
BF16 数据类型一般在 CPU、GPU 上均有支持,可在 cpu、gpu 目录下的相关文件中添加 FP16 数据支持。
检索方式。
同 1.b.i 相同,采用文件名进行查找。如 Abs 相关文件为 abs_kernel.cu
2.2 引入所需的头文件¶
为了使用 FP16/BF16 数据类型,需要在 GPU 源文件中引入下列头文件之一。其中 3 中定义了 FP16/BF16 数据类型,1 包含 2 包含 3。引入这些文件后,可以使用 phi::dtype::float16 来表示 FP16 数据类型,可以使用 phi::dtype::bfloat16 来表示 BF16 数据类型。
paddle/phi/core/device_context.h
paddle/phi/common/data_type.h
FP16 数据类型:paddle/phi/common/float16.h
BF16 数据类型:paddle/phi/common/bfloat16.h
2.3 在 Kernel 注册处添加 FP16/BF16 数据类型支持¶
每一个 GPU 源文件的末尾,都有用来进行 Kernels 注册的宏 PD_REGISTER_KERNEL。如 Abs 的注册宏代码 2-1。
PD_REGISTER_KERNEL(abs,
GPU,
ALL_LAYOUT,
phi::AbsKernel,
float,
double,
int,
int64_t,
phi::dtype::float16,
phi::dtype::complex<float>,
phi::dtype::complex<double>) {}
其中 phi::AbsKernel 是 abs 对应的具体 GPU 实现函数,在这之后的 float, double, int, ... 等为 abs 所支持的数据类型。因此要扩充 FP16 数据类型支持,需要在该处添加 phi::dtype::float16 数据类型。如果需要扩充 BF16 数据类型的支持,可添加 phi::dtype::bfloat16。
2.4 函数中添加 FP16/BF16 数据实现的特化支持¶
在注册时添加 FP16/BF16 的数据类型支持后,在对应的实现中也应添加对应的支持。
在 Paddle 中,各个 Kernel 的实现采用模版函数实现,函数所支持的数据类型也以模版参数的形式进行传入。因此可以自行编译出支持 FP16/BF16 实现的代码。但为了提升 FP16/BF16 计算的精度,在涉及数学计算函数和归约计算时,需要我们对 FP16/BF16 算子进行特化。
2.4.1 数学计算函数¶
数学计算函数是对于输入按照数学运算规则进行求解。Paddle 中的实现的大部分基本数学算子最终均归结于对 Math 库中的数学函数的调用。关于数学计算函数在 FP32 和 FP16 下的计算结果误差对比可参考附录。
2.4.1.1 存在问题¶
部分函数在 FP16/BF16 下相比 FP32 误差较高。典型的数学函数有 reciprocal、exp、expm1、tan、cosh、sinh、square、tanh_shrink。
部分函数会产生较高的数值输出,FP16 容易造成上溢出。典型的数学函数有 exp、expm1、square、tan、atanh、cosh、sinh。
2.4.1.2 特化实现代码¶
数学计算函数通常实现时, 需要将 FP16/BF16 格式转换为 FP32 格式,然后利用 FP32 作为输入计算数值结果,后再将结果转换为 FP16/BF16 格式作为输出 。以 Cos 函数的实现为例。
template <typename T, typename Context, typename Functor>
void ActivationGPUImpl(const Context& dev_ctx,
const DenseTensor& x,
DenseTensor* out,
const Functor& functor) {
PADDLE_ENFORCE_NOT_NULL(out,
errors::NotFound("Output Out should not be nullptr"));
dev_ctx.template Alloc<T>(out);
std::vector<const DenseTensor*> ins = {&x};
std::vector<DenseTensor*> outs = {out};
funcs::ElementwiseKernel<T>(dev_ctx, ins, &outs, functor);
}
template <typename T>
struct CudaCosFunctor {
using MPType = typename phi::dtype::MPTypeTrait<T>::Type;
__device__ __forceinline__ T operator()(const T arg_x) const {
MPType x = static_cast<MPType>(arg_x);
return static_cast<T>(cos(x));
}
};
template <typename T, typename Context>
void CosKernel(const Context& dev_ctx, const DenseTensor& x, DenseTensor* out) {
funcs::CudaCosFunctor<T> functor;
ActivationGPUImpl<T, Context, funcs::CudaCosFunctor<T>>(
dev_ctx, x, out, functor);
}
关于 MPTypeTrait 的定义可参考附录
2.4.2 归约计算¶
归约计算往往会设计大量元素参与运算,在这种情况下,很容易出现误差的累积,对于低精度计算并不友好。
2.4.2.1 存在问题¶
具有较多输入参数的大规模归约场景对浮点数的精度影响较大,主要有两个方面。
受限于 FP16/BF16 的低精度,大规模浮点归约的后期,容易形成“截断上界”,导致频繁的浮点数舍入行为。
大规模浮点规约因为浮点计算次数较多,容易累积误差,使得误差越来越大。
2.4.2.2 特化函数实现¶
最好 使用 FP32 格式进行归约。 以 add_n 为例,增添转换为 FP32 数据类型进行归约的一个建议的实现框架可以参考代码 2-3。
template <class T>
__global__ void SumArrayCUDAKernel(
T **in, T *out, int64_t N, size_t in_size, bool read_dst) {
using MPType = typename phi::dtype::MPTypeTrait<T>::Type;
int id = blockIdx.x * blockDim.x + threadIdx.x;
while (id < N) {
MPType total(read_dst ? static_cast<MPType>(out[id]) : static_cast<MPType>(0));
for (int i = 0; i < in_size; ++i) {
const T *tmp = in[i];
if (tmp) {
total += static_cast<MPType>(tmp[id]);
}
}
out[id] = static_cast<T>(total);
id += blockDim.x * gridDim.x;
}
}
template <typename T, typename Context>
void AddNKernel(const Context &dev_ctx,
const std::vector<const TensorBase *> &x,
DenseTensor *out) {
...... //pre-dealing
SumArrayCUDAKernel<T><<<grids, blocks, 0, stream>>>(in_array_data,
out->data<T>(),
lod_length,
in_data.size(),
dst_write | in_place);
...... //post-dealing
}
关于 MPTypeTrait 的定义可参考附录
三、附录¶
3.1 关于 MPTypeTrait 实现¶
MPtypeTrait 可以按照代码 3-1 进行实现,在传入 FP16/BF16 类型时,在类内部定义 FP32 类型。
源代码链接:https://github.com/PaddlePaddle/Paddle/blob/develop/paddle/phi/common/amp_type_traits.h
template <typename T>
class MPTypeTrait {
public:
using Type = T;
};
template <>
class MPTypeTrait<phi::dtype::float16> {
public:
using Type = float;
};
template <>
class MPTypeTrait<phi::dtype::bfloat16> {
public:
using Type = float;
};
3.2 关于__hisinf 和__hisnan¶
3.2.1 __hisinf¶
__device__ int __hisinf(const __half a)
定义:检查输入的 half 类型的参数是否为 INF
参数:half 类型,只读属性
返回:int 类型,其中 0 表示非 INF,1 表示+INF,-1 表示-INF
3.2.2 __hisnan¶
__device__ bool __hisnan ( const __half a )
定义:检查输入的 half 类型的参数是否为 NAN
参数:half 类型,只读属性
返回:bool 类型,true 表示是 NAN,false 表示非 NAN
3.3 基本数学函数在 FP32 和 FP16 的误差对比¶
基本数学计算函数在 FP16 格式下与 FP32 格式下计算结果的误差
| 算子 | 最大绝对误差 | 最大相对误差 | 平均绝对误差 | 平均相对误差 |
|---|---|---|---|---|
| sin/cos/atan/acosh/asinh/tanh/acos/asin/atanh | 0.000244~0.003905 | 0.000486~0.000517 | 5.85E-05~0.001138 | 0.000115~0.000179 |
| log2/log10/log1p | 0.001953~0.0033905 | 0.000482~0.000487 | 0.0004~0.001258 | 0.000171~0.000175 |
| floor/round/relu/ceil | 0 | 0 | 0 | 0 |
| sqrt/rsqrt | 0.031227~0.062485 | 0.000488 | 0.002071~0.004158 | 0.000172~0.000179 |
| exp/expm1/tan/cosh/sinh/reciprocal/square/tanh_shrink | 1~16 | 0.000486~1 | 0.000786~0.378427 | 9.18E-05~0.082869 |
| logsigmoid/sigmoid/silu/softsign | 0.000701~0.002665 | 0.000486~0.000945 | 6.55E-05~9.96E-05 | 0.000104~0.000203 |
注:
其中我们将数学函数归类为三角函数,对数函数,舍入函数,指数函数进行了测试,其中误差相对较大的 exp/expm1(红色标注)函数等我们将其提取出来放在了一组,另外其他一些未归类的 sigmoid 等误差相对较低也同一成了一组
以上测试均基于 Paddle 的 Python 模块进行
3.4 基本数学函数在 FP32 和 FP16 的误差对比¶
FP32 转 FP16 的统计误差:
包含非规规格情况下($2^{-24}\sim65504$):
| 最大绝对误差 | 最大相对误差 | 平均绝对误差 | 平均相对误差 |
|---|---|---|---|
| 16 | 0.33289 | 0.38871 | 0.008834 |
仅规格化数情况下($2^{-14}\sim65504$):
| 最大绝对误差 | 最大相对误差 | 平均绝对误差 | 平均相对误差 |
|---|---|---|---|
| 16 | 0.00048 | 0.51876 | 0.000175 |
注:
绝对误差采用 FP32 和转换后的 FP16 的距离
相对误差采用 FP32 和转换后的 FP16 的距离相对于 FP32 的比重
FP32 转 FP16 理论上的最大相对误差可参考实数转 FP16 的情况
实数转 FP16 在理论上单次的最大相对舍入误差(规格化下): $2^{-11}$
实数转 FP32 在理论上单次的最大相对舍入误差(规格化下): $2^{-24}$
实数转 FP16 在理论上单次的最大相对舍入误差(非规格化下):0.5
实数转 FP32 在理论上单次的最大相对舍入误差(非规格化下):0.5
延伸:FP16 和 FP32 精度对比时,应当采用相对误差为度量尺度,小于最大相对误差,相对误差可以保证在一定的范围内,但是绝对误差的范围本身的差距太大了,并不适合做度量尺度。