模型组网¶
模型组网是深度学习任务中的重要一环,该环节定义了神经网络的层次结构、数据从输入到输出的计算过程(即前向计算)等。
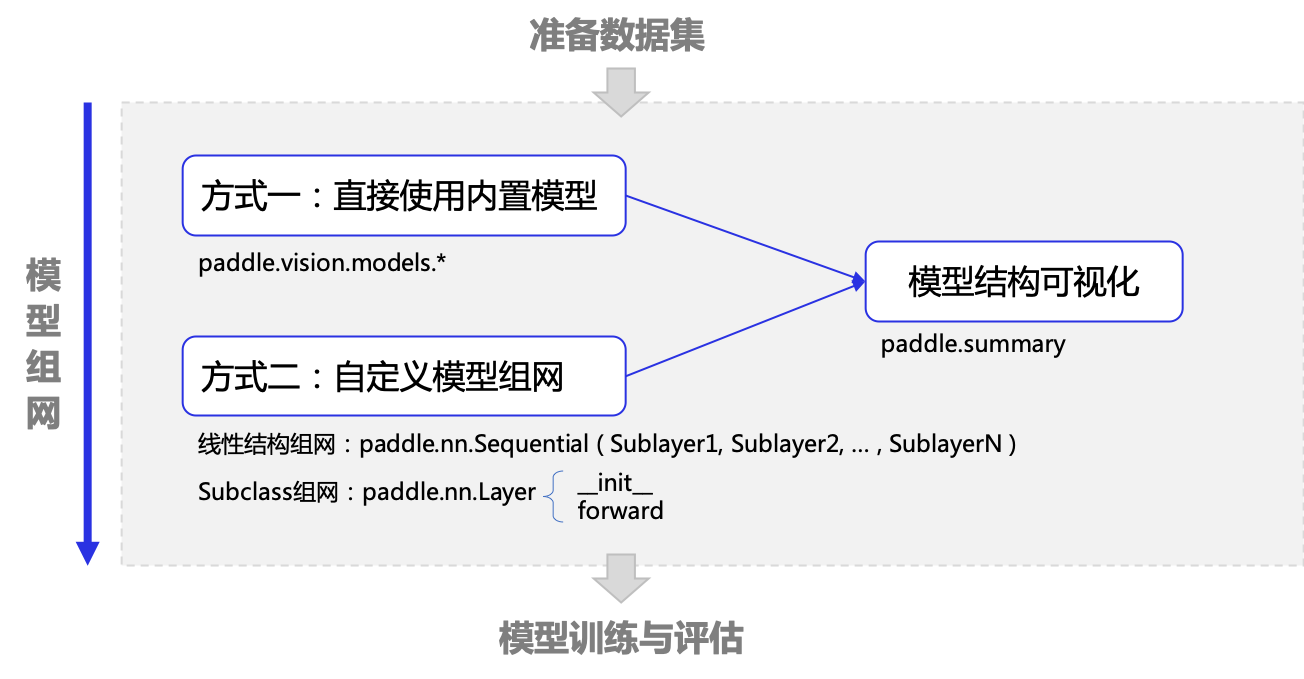
飞桨框架提供了多种模型组网方式,本文介绍如下几种常见用法:
直接使用内置模型
使用 paddle.nn.Sequential 组网
使用 paddle.nn.Layer 组网
另外飞桨框架提供了 paddle.summary 函数方便查看网络结构、每层的输入输出 shape 和参数信息。
一、直接使用内置模型¶
飞桨框架目前在 paddle.vision.models 下内置了计算机视觉领域的一些经典模型,只需一行代码即可完成网络构建和初始化,适合完成一些简单的深度学习任务,满足深度学习初阶用户感受模型的输入和输出形式、了解模型的性能。
import paddle
print('飞桨框架内置模型:', paddle.vision.models.__all__)
飞桨框架内置模型: ['ResNet', 'resnet18', 'resnet34', 'resnet50', 'resnet101', 'resnet152', 'VGG', 'vgg11', 'vgg13', 'vgg16', 'vgg19', 'MobileNetV1', 'mobilenet_v1', 'MobileNetV2', 'mobilenet_v2', 'LeNet']
以 LeNet 模型为例,可通过如下代码组网:
# 模型组网并初始化网络
lenet = paddle.vision.models.LeNet(num_classes=10)
# 可视化模型组网结构和参数
paddle.summary(lenet,(1, 1, 28, 28))
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Conv2D-1 [[1, 1, 28, 28]] [1, 6, 28, 28] 60
ReLU-1 [[1, 6, 28, 28]] [1, 6, 28, 28] 0
MaxPool2D-1 [[1, 6, 28, 28]] [1, 6, 14, 14] 0
Conv2D-2 [[1, 6, 14, 14]] [1, 16, 10, 10] 2,416
ReLU-2 [[1, 16, 10, 10]] [1, 16, 10, 10] 0
MaxPool2D-2 [[1, 16, 10, 10]] [1, 16, 5, 5] 0
Linear-1 [[1, 400]] [1, 120] 48,120
Linear-2 [[1, 120]] [1, 84] 10,164
Linear-3 [[1, 84]] [1, 10] 850
===========================================================================
Total params: 61,610
Trainable params: 61,610
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
---------------------------------------------------------------------------
{'total_params': 61610, 'trainable_params': 61610}
通过 paddle.summary 可清晰地查看神经网络层次结构、每一层的输入数据和输出数据的形状(Shape)、模型的参数量(Params)等信息,方便可视化地了解模型结构、分析数据计算和传递过程。从以上结果可以看出,LeNet 模型包含 2个Conv2D 卷积层、2个ReLU 激活层、2个MaxPool2D 池化层以及3个Linear 全连接层,这些层通过堆叠形成了 LeNet 模型,对应网络结构如下图所示。
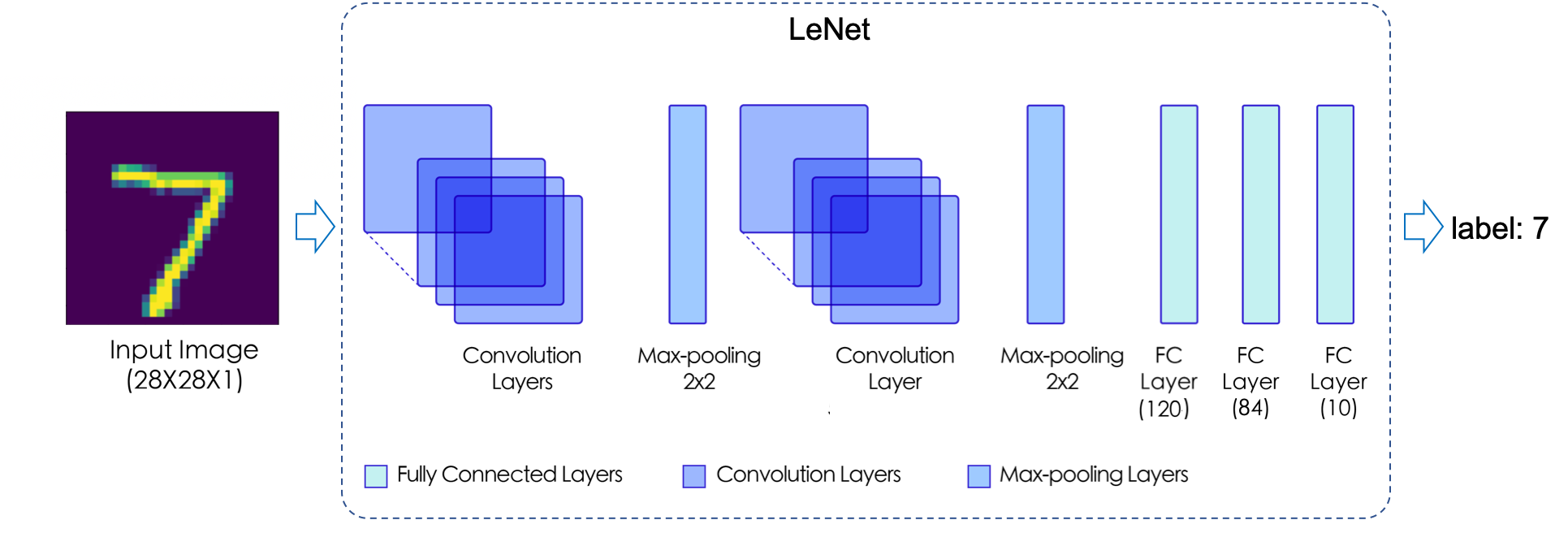
图 1:LeNet 网络结构示意图
二、Paddle.nn 介绍¶
经典模型可以满足一些简单深度学习任务的需求,然后更多情况下,需要使用深度学习框架构建一个自己的神经网络,这时可以使用飞桨框架 paddle.nn 下的 API 构建网络,该目录下定义了丰富的神经网络层和相关函数 API,如卷积网络相关的 Conv1D、Conv2D、Conv3D,循环神经网络相关的 RNN、LSTM、GRU 等,方便组网调用,详细清单可在 API 文档 中查看。
飞桨提供继承类(class)的方式构建网络,并提供了几个基类,如:paddle.nn.Sequential、 paddle.nn.Layer 等,构建一个继承基类的子类,并在子类中添加层(layer,如卷积层、全连接层等)可实现网络的构建,不同基类对应不同的组网方式,本节介绍如下两种常用方法:
使用 paddle.nn.Sequential 组网:构建顺序的线性网络结构(如 LeNet、AlexNet 和 VGG)时,可以选择该方式。相比于 Layer 方式 ,Sequential 方式可以用更少的代码完成线性网络的构建。
使用 paddle.nn.Layer 组网(推荐):构建一些比较复杂的网络结构时,可以选择该方式。相比于 Sequential 方式,Layer 方式可以更灵活地组建各种网络结构。Sequential 方式搭建的网络也可以作为子网加入 Layer 方式的组网中。
三、使用 paddle.nn.Sequential 组网¶
构建顺序的线性网络结构时,可以选择该方式,只需要按模型的结构顺序,一层一层加到 paddle.nn.Sequential 子类中即可。
参照前面图 1 所示的 LeNet 模型结构,构建该网络结构的代码如下:
from paddle import nn
# 使用 paddle.nn.Sequential 构建 LeNet 模型
lenet_Sequential = nn.Sequential(
nn.Conv2D(1, 6, 3, stride=1, padding=1),
nn.ReLU(),
nn.MaxPool2D(2, 2),
nn.Conv2D(6, 16, 5, stride=1, padding=0),
nn.ReLU(),
nn.MaxPool2D(2, 2),
nn.Flatten(),
nn.Linear(400, 120),
nn.Linear(120, 84),
nn.Linear(84, 10)
)
# 可视化模型组网结构和参数
paddle.summary(lenet_Sequential,(1, 1, 28, 28))
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Conv2D-3 [[1, 1, 28, 28]] [1, 6, 28, 28] 60
ReLU-3 [[1, 6, 28, 28]] [1, 6, 28, 28] 0
MaxPool2D-3 [[1, 6, 28, 28]] [1, 6, 14, 14] 0
Conv2D-4 [[1, 6, 14, 14]] [1, 16, 10, 10] 2,416
ReLU-4 [[1, 16, 10, 10]] [1, 16, 10, 10] 0
MaxPool2D-4 [[1, 16, 10, 10]] [1, 16, 5, 5] 0
Flatten-1 [[1, 16, 5, 5]] [1, 400] 0
Linear-4 [[1, 400]] [1, 120] 48,120
Linear-5 [[1, 120]] [1, 84] 10,164
Linear-6 [[1, 84]] [1, 10] 850
===========================================================================
Total params: 61,610
Trainable params: 61,610
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
---------------------------------------------------------------------------
{'total_params': 61610, 'trainable_params': 61610}
使用 Sequential 组网时,会自动按照层次堆叠顺序完成网络的前向计算过程,简略了定义前向计算函数的代码。由于 Sequential 组网只能完成简单的线性结构模型,所以对于需要进行分支判断的模型需要使用 paddle.nn.Layer 组网方式实现。
四、使用 paddle.nn.Layer 组网¶
构建一些比较复杂的网络结构时,可以选择该方式,组网包括三个步骤:
创建一个继承自 paddle.nn.Layer 的类;
在类的构造函数
__init__中定义组网用到的神经网络层(layer);在类的前向计算函数
forward中使用定义好的 layer 执行前向计算。
仍然以 LeNet 模型为例,使用 paddle.nn.Layer 组网的代码如下:
# 使用 Subclass 方式构建 LeNet 模型
class LeNet(nn.Layer):
def __init__(self, num_classes=10):
super(LeNet, self).__init__()
self.num_classes = num_classes
# 构建 features 子网,用于对输入图像进行特征提取
self.features = nn.Sequential(
nn.Conv2D(
1, 6, 3, stride=1, padding=1),
nn.ReLU(),
nn.MaxPool2D(2, 2),
nn.Conv2D(
6, 16, 5, stride=1, padding=0),
nn.ReLU(),
nn.MaxPool2D(2, 2))
# 构建 linear 子网,用于分类
if num_classes > 0:
self.linear = nn.Sequential(
nn.Linear(400, 120),
nn.Linear(120, 84),
nn.Linear(84, num_classes)
)
# 执行前向计算
def forward(self, inputs):
x = self.features(inputs)
if self.num_classes > 0:
x = paddle.flatten(x, 1)
x = self.linear(x)
return x
lenet_SubClass = LeNet()
# 可视化模型组网结构和参数
params_info = paddle.summary(lenet_SubClass,(1, 1, 28, 28))
print(params_info)
---------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===========================================================================
Conv2D-5 [[1, 1, 28, 28]] [1, 6, 28, 28] 60
ReLU-5 [[1, 6, 28, 28]] [1, 6, 28, 28] 0
MaxPool2D-5 [[1, 6, 28, 28]] [1, 6, 14, 14] 0
Conv2D-6 [[1, 6, 14, 14]] [1, 16, 10, 10] 2,416
ReLU-6 [[1, 16, 10, 10]] [1, 16, 10, 10] 0
MaxPool2D-6 [[1, 16, 10, 10]] [1, 16, 5, 5] 0
Linear-7 [[1, 400]] [1, 120] 48,120
Linear-8 [[1, 120]] [1, 84] 10,164
Linear-9 [[1, 84]] [1, 10] 850
===========================================================================
Total params: 61,610
Trainable params: 61,610
Non-trainable params: 0
---------------------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
---------------------------------------------------------------------------
{'total_params': 61610, 'trainable_params': 61610}
在上面的代码中,将 LeNet 分为了 features 和 linear 两个子网,features 用于对输入图像进行特征提取,linear 用于输出十个数字的分类。
扩展:模型的层(Layer)¶
模型组网中一个关键组成就是神经网络层,不同的神经网络层组合在一起,从输入的数据样本中习得数据内在规律,最终输出预测结果。每个层从前一层获得输入数据,然后输出结果作为下一层的输入,并且大多数层包含可调的参数,在反向传播梯度时更新参数。
在飞桨框架中内置了丰富的神经网络层,用类(class)的方式表示,构建模型时可直接作为实例添加到子类中,只需设置一些必要的参数,并定义前向计算函数即可,反向传播和参数保存由框架自动完成。
下面展开介绍几个常用的神经网络层。
Conv2D¶
Conv2D (二维卷积层)主要用于对输入的特征图进行卷积操作,广泛用于深度学习网络中。Conv2D 根据输入、卷积核、步长(stride)、填充(padding)、空洞大小(dilations)等参数计算输出特征层大小。输入和输出是 NCHW 或 NHWC 格式,其中 N 是 batchsize 大小,C 是通道数,H 是特征高度,W 是特征宽度。
x = paddle.uniform((2, 3, 8, 8), dtype='float32', min=-1., max=1.)
conv = nn.Conv2D(3, 6, (3, 3), stride=2) # 卷积层输入通道数为3,输出通道数为6,卷积核尺寸为3*3,步长为2
y = conv(x) # 输入数据x
y = y.numpy()
print(y.shape)
(2, 6, 3, 3)
MaxPool2D¶
MaxPool2D (二维最大池化层)主要用于缩小特征图大小,根据 kernel_size 参数指定的窗口大小,对窗口内特征图进行取最大值的操作。
x = paddle.uniform((2, 3, 8, 8), dtype='float32', min=-1., max=1.)
pool = nn.MaxPool2D(3, stride=2) # 池化核尺寸为3*3,步长为2
y = pool(x) #输入数据x
y = y.numpy()
print(y.shape)
(2, 3, 3, 3)
扩展:模型的参数(Parameter)¶
在飞桨框架中,可通过网络的 parameters() 和 named_parameters() 方法获取网络在训练期间优化的所有参数(权重 weight 和偏置 bias),通过这些方法可以实现对网络更加精细化的控制,如设置某些层的参数不更新。
下面这段示例代码,通过 named_parameters() 获取了 LeNet 网络所有参数的名字和值,打印出了参数的名字(name)和形状(shape)。
for name, param in lenet.named_parameters():
print(f"Layer: {name} | Size: {param.shape}")
Layer: features.0.weight | Size: [6, 1, 3, 3]
Layer: features.0.bias | Size: [6]
Layer: features.3.weight | Size: [16, 6, 5, 5]
Layer: features.3.bias | Size: [16]
Layer: fc.0.weight | Size: [400, 120]
Layer: fc.0.bias | Size: [120]
Layer: fc.1.weight | Size: [120, 84]
Layer: fc.1.bias | Size: [84]
Layer: fc.2.weight | Size: [84, 10]
Layer: fc.2.bias | Size: [10]