paddle.incubate.autograd¶

paddle.incubate.autograd 提供支持高阶的反向及前向自动微分相关 API，是飞桨框架对高阶自动微分进行探索与升级。当前处于孵化状态，API 签名及相关功能可能会发生变化，功能尚不完善，如果想自行实现相关模型、探索自动微分机制，请仔细阅读下述使用方法及使用限制。

推荐用法¶

第一步：导入依赖。使用 paddle.incubate.autograd.enable_prim() 打开自动微分开关。

          import numpy as np
import paddle

paddle.enable_static()
paddle.incubate.autograd.enable_prim()

第二步：编写组网代码。以单层的全联接网络为例，MyNet 继承自 paddle.nn.Layer ，在 __init__ 方法中初始化网络参数，在 forward 方法中实现前向运行逻辑。注意，当前自动微分仅支持部分飞桨 API，主要覆盖全联接网络和一些激活函数，当前支持的飞桨 API 列表参考支持的飞桨 API。

          class MyNet(paddle.nn.Layer):
    def __init__(self):
        super(MyNet, self).__init__()
        self.weight = self.create_parameter(shape=(2,2), dtype='float32', is_bias=False)
        self.bias = self.create_parameter(shape=(2,2), dtype='float32', is_bias=True)
        self.add_parameter("weight", self.weight)
        self.add_parameter("bias", self.bias)

    def forward(self, x):
        y = paddle.matmul(x, self.weight) + self.bias
        return paddle.tanh(y)

         

第三步：创建网络及声明输入数据，执行前向计算过程。注意，输入数据目前尚不支持可变形状，即类似 paddle.static.data('x', shape=(None, 2), dtype='float32')写法，如果您的输入数据形状会变化可以参考附 1 写法。

          x = paddle.static.data('x', shape=(2,2), dtype='float32')
net = MyNet()
y = net(x)

         

第四步：计算 Loss 并进行优化。为了演示高阶微分用法，此处 Loss 定义中使用了 paddle.incubate.autograd.grad API 计算 y 对 x 二阶微分，使用 L2 norm 归一化，然后用 Adam 优化器进行优化。目前已支持高阶的反向微分和前向微分，相关 API 列表参考自动微分 API 。

          grad1 = paddle.incubate.autograd.grad(y, x)
grad2 = paddle.incubate.autograd.grad(grad1, x)
loss = paddle.norm(grad2, p=2)

opt = paddle.optimizer.Adam(0.01)
opt.minimize(loss)

         

第五步：创建执行器，加载输入数据，执行网络训练。为了演示训练过程，此处模拟一个长度为 10 的输入数据，迭代执行网络，进行训练，并打印相关结果。

          # 创建执行器
exe = paddle.static.Executor()
# 执行一次默认 startup program，初始化网络参数
exe.run(paddle.static.default_startup_program())

# 模拟形状固定的长度为 10 的输入数据
data = [np.random.rand(2,2).astype(np.float32) for i in range(10)]
# feed 网络输入数据，fetch_list 中指定想要 fetch 的结果，迭代执行网络进行训练
for i, x in enumerate(data):
    loss_val, = exe.run(feed={'x': x}, fetch_list=[loss])
    print("iter: ", i+1, " loss: ", loss_val)

         

自动微分 API 列表¶

API 名称	API 功能
paddle.incubate.autograd.grad	反向模式自动微分
paddle.incubate.autograd.forward_grad	前向模式自动微分
paddle.incubate.autograd.Jacobian	一阶微分通用形式
paddle.incubate.autograd.Hessian	二阶微分通用形式

除上述 API 之外，还包含两个开关类 API, 用于打开/关闭自动微分。

API 名称	API 功能
paddle.incubate.autograd.enable_prim	打开自动微分
paddle.incubate.autograd.disable_prim	关闭自动微分

使用反向微分 API paddle.incubate.autograd.grad 计算 tanh 高阶导数

          import paddle
import numpy as np

paddle.enable_static() # 开启静态图
paddle.incubate.autograd.enable_prim() # 开启自动微分

# 组网代码
x = paddle.static.data('x', shape=((1, )), dtype=paddle.float32)
y = paddle.tanh(x)
grad1 = paddle.incubate.autograd.grad(y, x)     # 一阶微分
grad2 = paddle.incubate.autograd.grad(grad1, x) # 二阶微分
grad3 = paddle.incubate.autograd.grad(grad2, x) # 三阶微分

feed = {'x': np.ones((1,)).astype(np.float32)}
fetch_list = [grad1, grad2, grad3]
exe = paddle.static.Executor()
grad1, grad2, grad3 = exe.run(feed=feed, fetch_list=fetch_list)

print(grad1, grad2, grad3)
# [0.41997433] [-0.6397] [0.6216267]

         

使用前向微分 paddle.incubate.autograd.forward_grad 计算输出元素数量大于输入情况，前向微分相关概念及使用场景参考 https://en.wikipedia.org/wiki/Automatic_differentiation

          import paddle
import numpy as np

paddle.enable_static() # 开启静态图
paddle.incubate.autograd.enable_prim() # 开启自动微分

# 组网代码
def func(x): # 单输入多输出函数
    return x+x, x*x, paddle.tanh(x)

x = paddle.static.data('x', shape=((1, )), dtype=paddle.float32)
y = func(x)
# 前向微分遍历一次计算图可以计算所有输出对一个输入的导数
out = paddle.incubate.autograd.forward_grad(y, x)

exe = paddle.static.Executor()
out = exe.run(feed={'x': np.random.rand(1).astype(np.float32)}, fetch_list=[out])
print(out)

         

使用 paddle.incubate.autograd.Jacobian 计算 Jacobian 矩阵

          import paddle
import numpy as np

paddle.enable_static() # 开启静态图
paddle.incubate.autograd.enable_prim() # 开启自动微分

# 组网代码
x = paddle.static.data('x', shape=((2,8)), dtype=paddle.float32)
y = paddle.static.data('y', shape=((2,8)), dtype=paddle.float32)
# 创建 Jaocbian 实例，此时并不发生计算，支持 batch
J = paddle.incubate.autograd.Jacobian(paddle.multiply, (x,y), is_batched=True)
# 惰性计算，有效提升计算速度，减少显存开销
row = J[:, 0, :] # 获取第一行数据，并缓存
col = J[:, 0:3, :] # 获取前三行，第一行结果上次计算中已经缓存
all = J[:] # 获取所有元素，前三行数据已经缓存


feed = {
'x': np.random.randn(2,8).astype(np.float32),
'y': np.random.randn(2,8).astype(np.float32)
}
fetch_list = [row, col, all]
exe = paddle.static.Executor()
row, col, all = exe.run(feed=feed, fetch_list=fetch_list)

         

当前支持的飞桨 API¶

目前只支持部分飞桨 API，主要覆盖全联接网络和一些激活函数，具体如下：

API 路径	链接
paddle.reshape	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/reshape_cn.html#reshape
paddle.broadcast_to	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/broadcast_to_cn.html#broadcast-to
paddle.transpose	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/transpose_cn.html#transpose
paddle.split	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/split_cn.html#split
paddle.concat	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/concat_cn.html#concat
paddle.slice	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/strided_slice_cn.html#strided-slice
paddle.assign	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/assign_cn.html#assign
paddle.gather	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/gather_cn.html#gather
paddle.add	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/add_cn.html#add
paddle.subtract	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/subtract_cn.html#subtract
paddle.multiply	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/multiply_cn.html#multiply
paddle.divide	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/divide_cn.html#divide
paddle.sqrt	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/sqrt_cn.html#sqrt
paddle.tanh	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/tanh_cn.html#tanh
paddle.matmul	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/matmul_cn.html#matmul
paddle.sin	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/sin_cn.html#sin
paddle.cos	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/cos_cn.html#cos
paddle.exp	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/exp_cn.html#exp
paddle.scale	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/scale_cn.html#scale
paddle.zeros_like	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/zeros_like_cn.html#zeros-like
paddle.index_select	https://www.paddlepaddle.org.cn/documentation/docs/zh/develop/api/paddle/index_select_cn.html#index-select
paddle.norm/p=2	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/linalg/norm_cn.html#norm
paddle.optimizer.Adam	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/optimizer/Adam_cn.html#adam
paddle.optimizer.SGD	https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/optimizer/SGD_cn.html#sgd

使用限制¶

输入数据不支持可变形状写法，如[None, 1]、[-1, 1]。如果训练数据形状是变化的，一种可行 Workaround 方案是根据不同数据形状创建不同网络，即在组网阶段将形状固定，具体参考附 1 代码。
我们尚未在 windows 平台进行完整验证和支持。
目前只支持使用 default_main_program 和 default_startup_program。
boradcast 语意尚未完整支持。

设计细节¶

在传统的深度学习任务中，神经网络的搭建分为前向和反向过程。通过深度学习框架的自动微分机制，对前向网络中的算子求一阶导数可以完成反向过程的搭建。在一些复杂的深度学习任务中，有时会使用到高阶导数。如，科学计算领域的深度学习任务中，由于引入偏微分方程组，往往需要使用到高阶导数。特别地，在输入数量大于输出数量时，反向微分更加高效；在输入数量小于输出数量时，前向微分更加高效. 为了更好地支持这些应用场景，需要深度学习框架具备高阶自动微分的能力，且支持前向和反向两种微分模式。

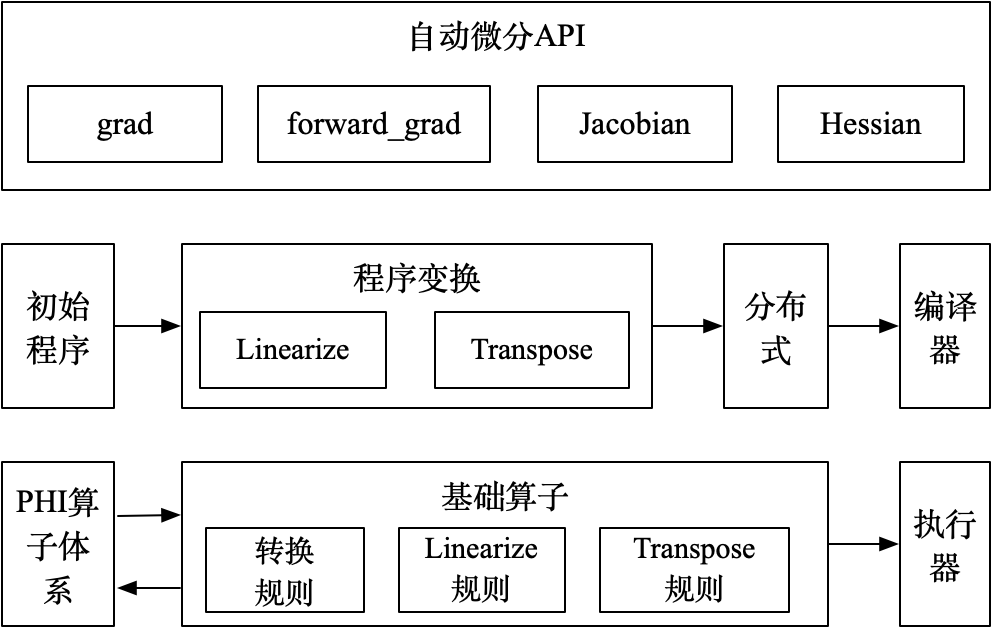
整体架构如下图：

基础算子体系：由初等函数组成，并定义对应的前向(Linearize)和反向(Transpose)规则，且前向和反向规则也基于基础算子实现；
程序变换：输入初始程序，Linearize 变换调用前向规则输出前向计算程序，Transpose 变换基于前向计算程序调用反向规则输出反向计算程序；
自动微分 API：提供前向、反向模式的高阶微分 API；

具体执行时，由 PHI 原生算子组成的程序，会拆解为基础算子组成的程序。然后在基础算子组成的程序之上，调用前向和反向规则，进行微分变换，输出前向和反向程序。如果是高阶微分，重复上述微分变换。最终输出的程序交由分布式和编译器进行处理后，由执行器进行执行。

RoadMap¶

目前基于自动微分基础算子的自动微分机制还在积极演进阶段，可预见的工作包括：

功能覆盖更多的组网 API
支持控制流
支持可变形状
支持动态图模式
调整编程范式和编程使用思路

欢迎持续关注或者参与共建。

附 1 可变形状的 Workaround 方案¶

由于当前尚支持声明可变形状数据，当您 feed 到网络的训练数据形状会发生变化时，需要遍历不同形状数据，将确定的数据形状输入到组网代码中，如下述代码中的 20-38 行。

          import numpy as np
import paddle


paddle.enable_static()
paddle.incubate.autograd.enable_prim()

class MyNet(paddle.nn.Layer):
    def __init__(self):
        super(MyNet, self).__init__()
        self.weight = self.create_parameter(shape=(2,2), dtype='float32', is_bias=False)
        self.bias = self.create_parameter(shape=(2,), dtype='float32', is_bias=True)
        self.add_parameter("weight", self.weight)
        self.add_parameter("bias", self.bias)

    def forward(self, x):
        y = paddle.matmul(x, self.weight) + self.bias
        return paddle.tanh(y)

# 模拟一个形状变化输入数据
data = [
    np.random.rand(3,2).astype(np.float32),
    np.random.rand(4,2).astype(np.float32),
    np.random.rand(5,2).astype(np.float32)
]

# 遍历输入数据，将形状作为 paddle.static.data 参数传入，此时形状是固定的
for i, input in enumerate(data):
    x = paddle.static.data(f'x{i}', shape=input.shape, dtype='float32')
    net = MyNet()
    y = net(x)

    grad1 = paddle.incubate.autograd.grad(y, x)
    grad2 = paddle.incubate.autograd.grad(grad1, x)
    loss = paddle.norm(grad2, p=2)

    opt = paddle.optimizer.Adam(0.01)
    opt.minimize(loss)

exe = paddle.static.Executor()
exe.run(paddle.static.default_startup_program())

for epoch in range(10):
    loss_val, = exe.run(feed={f'x{i}': x for i, x in enumerate(data)}, fetch_list=[loss])
    print("epoch: ", epoch+1, " loss: ", loss_val)

         