飞桨设计思想

本章节主要介绍飞桨深度学习框架的底层设计思想，通过本章学习，可以帮助用户理解飞桨框架的运作过程，以便于在实际业务需求中，更好地完成模型代码编写、调试以及基于飞桨进行二次开发。

飞桨设计思想的核心概念

下面我们先以传统的静态图执行过程为例，展现下飞桨框架内部的执行结构。静态图模式的思想是以程序代码完整描述一个网络结构和训练过程，然后将模型封装成一个Program交予执行器进行执行。本教程内容中绝大部分的建模代码均是动态图模式，动态图的模式则会使用Python原生的控制流语句，实时解释执行模型训练过程，两者的差别会在下一小节中更多介绍。

描述神经网络模型的Program，由多个Block（控制流结构）构成，每个Block是由Operator（算子）和数据表示Variable（变量）构成，经过串联形成从输入到输出的计算流。

• 飞桨采用类似于编程语言的抽象语法树的形式描述用户的神经网络配置，我们称之为Program。构建深度学习模型的代码时，将其中的计算模块写入Program中，可以理解为Program是模型计算的集合体。一个模型可以有多个Program，比如GAN模型。

• Program 又由嵌套的 Block 构成，Block是高级语言中变量作用域的概念，比如 if 条件语句下的代码可以视为是一个Block，Block是可以嵌套的。Block中又包括Operator 和 Variable。深度学习模型与Program、Block的关系如 图1 所示：

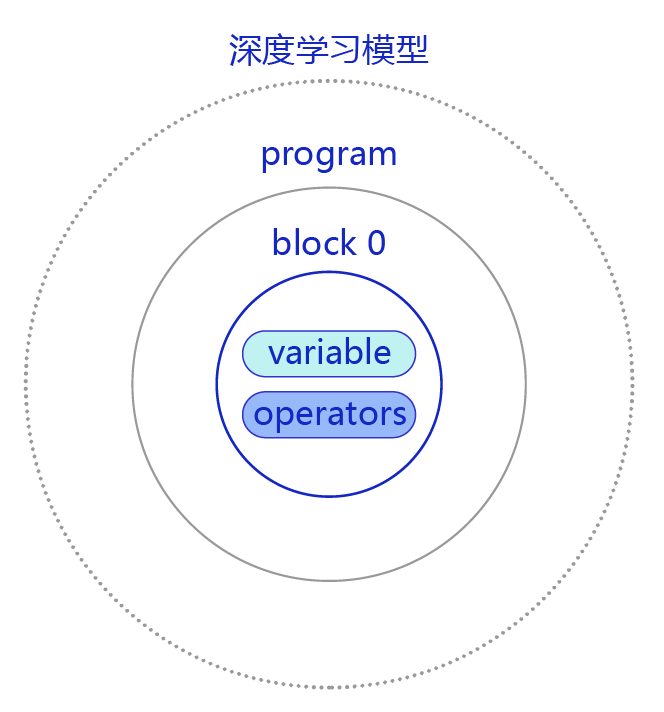
图1：深度学习模型与program、block三者关系示意

• 在一个Block中，飞桨将神经网络抽象为计算表示Operator（算子）和数据表示Variable（变量），如 图2 所示。神经网络的每层操作均由一个或若干Operator组成，每个Operator接收一系列的Variable作为输入，经计算后输出一系列的Variable。

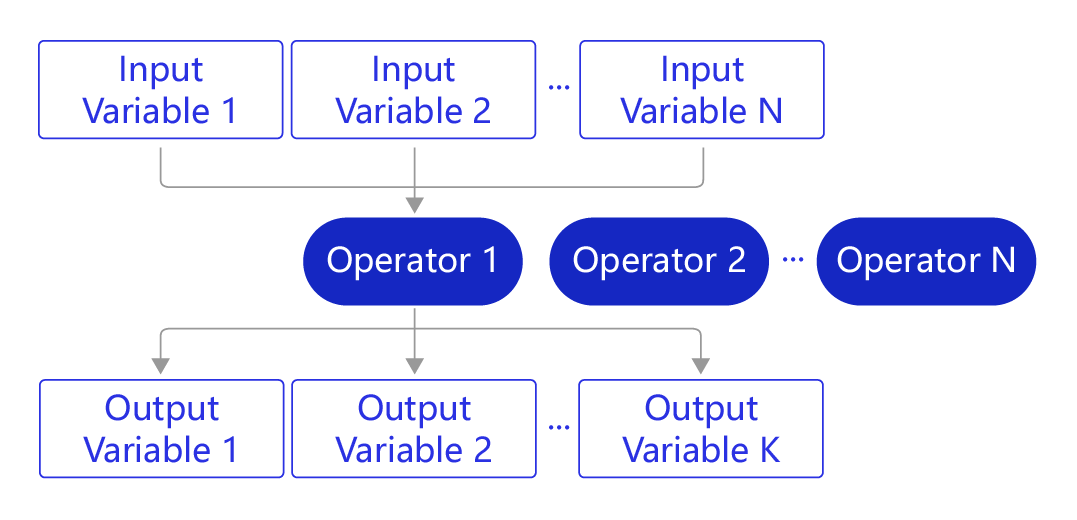
图2: OP和Variable的关系

关于Program具体的结构和包含的类型可参考设计实现framework.proto 。

构建深度学习模型时，用户只需定义前向计算网络、损失函数和优化算法，框架会自动生成前向计算和梯度优化的流程，该流程由初始化程序（startup_program）与主程序(main_program)实现。

一个Program的集合通常包含初始化程序（startup_program）与主程序(main_program)，默认情况下，飞桨的神经网络模型都包括两个program，分别是static.default_startup_program()以及static.default_main_program()，它们共享参数。 default_startup_program 只运行一次来初始化参数，训练时，default_main_program 在每个batch中运行并更新权重。

如何根据python代码构建Program

下面，我们通过几行代码说明飞桨是如何根据python代码构建Program的。

完成神经网络的构建一般离不开：构建训练数据，定义网络层定义，计算损失函数，声明优化器。 上述三种情况可以用几行代码说明：

# 声明数据
data = static.data(name='X', shape=[batch_size, 1], dtype='float32')
# 定义网络层
hidden = static.nn.fc(x=data, size=10)
# 计算损失函数
loss = paddle.mean(hidden)
# 声明优化器
sgd_opt = paddle.optimizer.SGD(learning_rate=0.01).minimize(loss)

每执行一行代码，飞桨都会在构建的program里添加variable和operator。

每行代码在Program里的影响如 图3 所示：

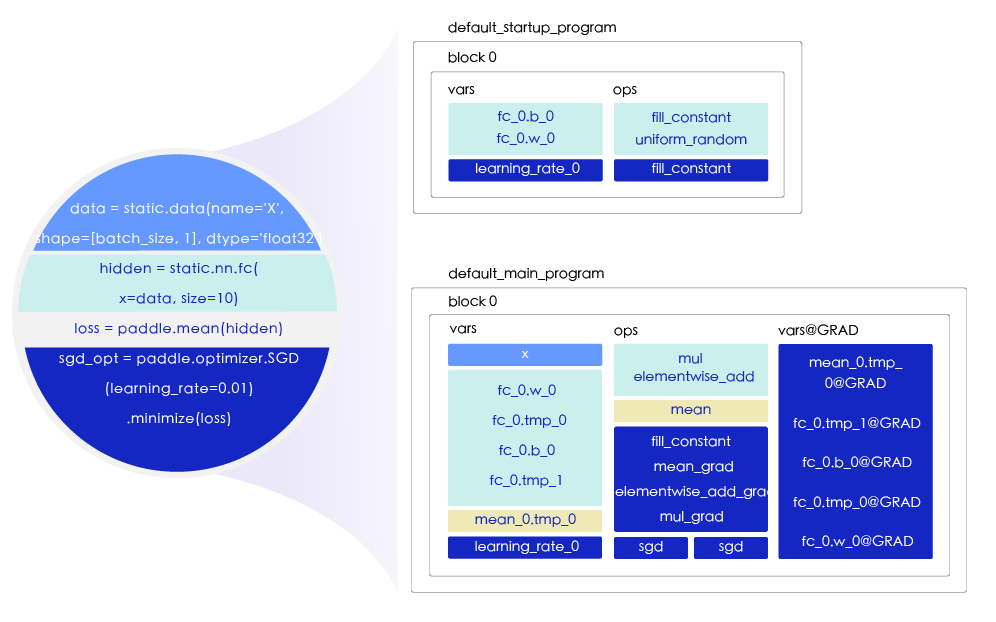
图3：每行代码在Program里的影响

图3 中，代码的颜色和Program中vars和ops中的颜色块相对应，比如：

1. 底纹为 颜色的代码是声明数据的代码，其定义了一个数据源节点，名字是X，所以在main_program中添加 X 这个variable。

2. 底纹为 颜色的代码是定义全连接网络层fc的代码，神经网络层是一种计算，所以它属于operator，全连接层由矩阵相乘运算和元素相加运算组成，因此，全连接层包括两个operator，分别是mul和elementwise_add，隶属于operator的范畴，所以该部分添加到ops的网格中。同时，网络层又包含可训练的参数，包括权重fc_0.w_0和偏置fc_0.b_0，这些参数均是待初始化的variable。另外，全连接层本身的operator会产生输出variable，即是新的variable fc_0.tmp。

3. 底纹为 颜色的代码表示损失函数计算，使用的是paddle.mean这个API，该API包含一个取平均的operator，同时有一个输出的Tensor，所以分别在ops和vars中添加了mean和mean_0.tmp_0。

4. 底纹为 颜色的代码表示定义优化器，优化器有输入参数学习率，内部计算时会将学习率以fill_constant这个API转换成variable。SGD涉及权重的梯度计算和参数更新，包含的operator较多（ops中绿色部分）。同时，SGD会给整个网络的计算图添加反向计算，所有可更新的variable都有对应的梯度变量vars@grad。

所以，飞桨中所有对数据的操作都由 Operator 表示，为了便于用户使用，在 Python 端，飞桨的 Operator 被一步封装到 paddle.Tensor和paddle.nn等模块（注：从Paddle 2.0版本开始）。用户可以使用飞桨提供的API快速完成算法的组网。

在组网时，飞桨在内部会不断的添加新的Variable和Operator到计算图里。直到计算图构建完成，在启动训练时，飞桨会按照Operator的顺序执行，直到完成训练。

下面，我们通过一个简单的矩阵乘法，观察Program的内容。

乍一看program的内容很难理解，但是不难发现其规律， 从打印的program中我们可以发现，program呈现字典形式的结构：

blocks{
    vars{
        """vars attribute"""
    }
    vars{
        """vars attribute"""
    }
    ops{
        """opeartors attribute"""
    }
    version{
        """other information"""
    }
}

上面的代码中，我们实现矩阵乘法，使用了飞桨的paddle.matmul API 来实现。从打印结果来看，Program中有一个block，block中包含了vars和ops，此处的vars一共有三个，分别是两个输入的矩阵变量，以及mul的输出变量，operator只有一个乘法mul运算。和上图中的结构一一对应。如果是更复杂的网络结构，其program也更加复杂。

下面运行上图中的代码，并打印program的内容到program.txt文件中。通过查看program中vars和ops，可以发现，和 图3 的说明一一对应。

飞桨声明式编程（静态图）与命令式编程（动态图）

从深度学习模型构建方式上看，飞桨支持声明式编程（静态图/Declarative programming）和命令式编程（动态图/Imperative programming）两种方式。二者的区别是：

• 静态图采用先编译后执行的方式。用户需预先定义完整的网络结构，再对网络结构进行编译优化后，才能执行获得计算结果。
• 动态图采用解析式的执行方式。用户无需预先定义完整的网络结构，每执行一行代码就可以获得代码的输出结果。

在飞桨设计上，把一个神经网络定义成一段类似程序的描述，就是在用户写程序的过程中，就定义了模型表达及计算。在静态图的控制流实现方面，飞桨借助自己实现的控制流OP而不是python原生的if else和for循环，这使得在飞桨中的定义的program即一个网络模型，可以有一个内部的表达，是可以全局优化编译执行的。考虑对开发者来讲，更愿意使用python原生控制流，飞桨也做了支持，并通过解释方式执行，这就是动态图。但整体上，我们两种编程范式是相对兼容统一的。

举例来说，假设用户写了一行代码：y=x+1。在静态图模式下，运行此代码只会往计算图中插入一个Tensor加1的Operator，此时Operator并未真正执行，无法获得y的计算结果。但在动态图模式下，所有Operator均是即时执行的，运行完代码后Operator已经执行完毕，用户可直接获得y的计算结果。

静态图模式和动态图模式的能力对比如下表所示：

对比项	静态图模式	动态图模式
是否可即时获得每层计算结果	否，必须构建完整网络后才能运行	是
调试难易性	欠佳，不易调试	结果即时，调试方便
性能	由于计算图完全确定，可优化的空间更多，性能更佳	计算图动态生成，图优化的灵活性受限，部分场景性能不如静态图
预测部署能力	可直接预测部署	不可直接预测部署，需要转换为静态图模型后再能部署

飞桨正逐步完善将动态图模式编写的模型，一键转变成静态图模式的功能，然后可方便地进行高性能的分布式训练和模型部署。

飞桨静态图

静态图核心架构

飞桨静态图核心架构分为Python前端和C++后端两个部分，如 图4 所示：

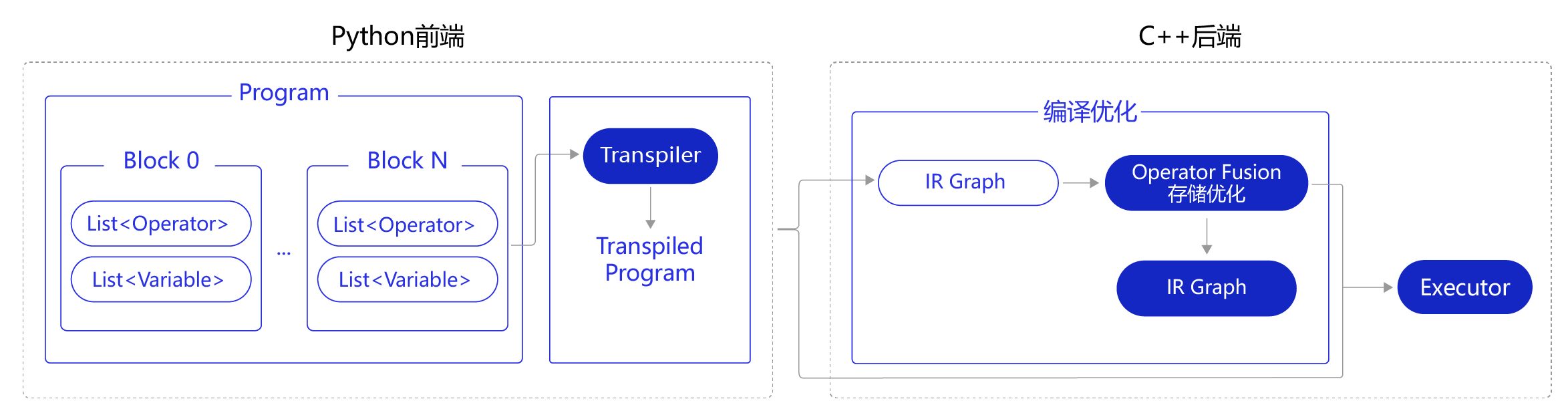
图4 飞桨静态图核心架构示意图

用户通过Python语言使用飞桨，但训练和预测的执行后端均为C++程序，这使得飞桨兼具用户轻松的编程体验和极高的执行效率。

- Python前端：

1. 在Python端，静态图模式是在形成Program的完整表达后，编译优化并交于执行器执行。Program由一系列的Block组成，每个Block包含各自的 Variable 和Operator。
2. （可选操作）Transpiler将用户定义的Program转换为Transpiled Program，如：分布式训练时，将原来的Program拆分为Parameter Server Program 和Trainer Program。在两者中均插入了通信的算子，用于不同训练服务器之间通信参数梯度的情况。

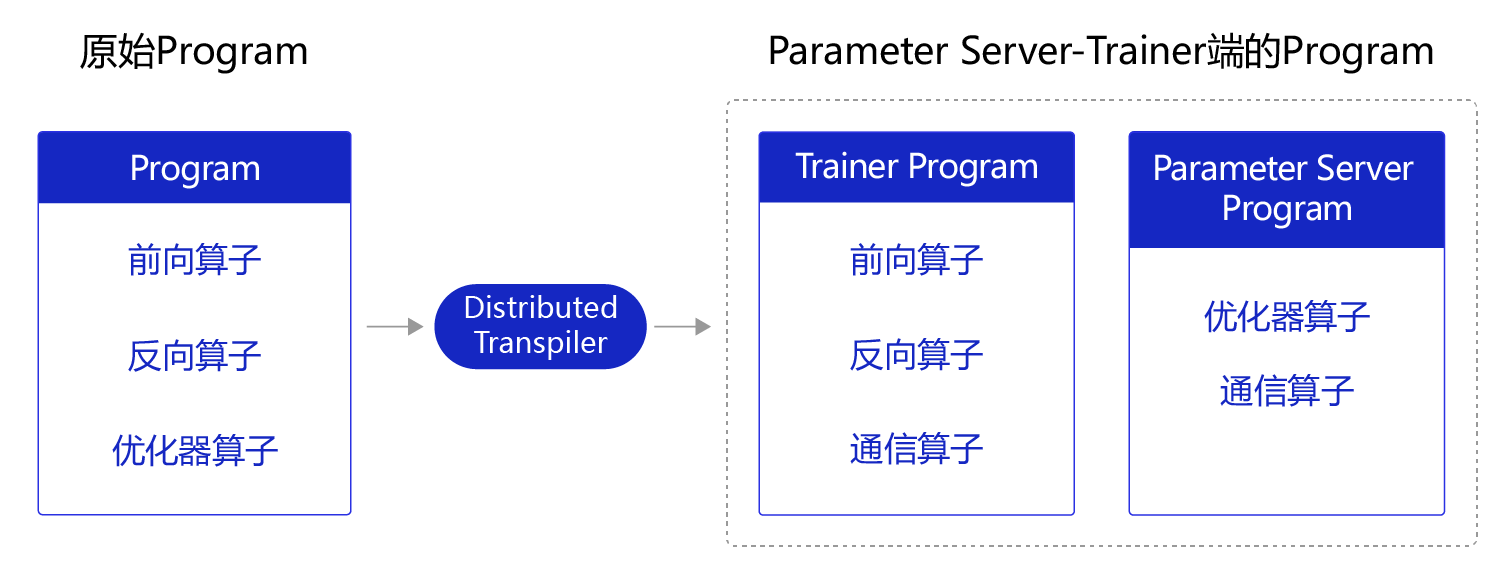
图5 原始Program经过特定的Transpiler形成特定功能的Program

- C++后端：

1. （可选操作）C++后端将Python端的Program转换为统一的中间表达（Intermediate Representation，IR Graph），并进行相应的编译优化，最终得到优化后可执行的计算图。其中，编译优化包括但不限于：

   • Operator Fusion：将网络中的两个或多个细粒度的算子融合为一个粗粒度算子。例如，表达式z = relu(x + y)对应着2个算子，即执行x + y运算的elementwise_add算子和激活函数relu算子。若将这2个算子融合为一个粗粒度的算子，一次性完成elementwise_add和relu这2个运算，可节省中间计算结果的存储、读取等过程，以及框架底层算子调度的开销，从而提升执行性能和效率。通俗点理解，读者在中小学做过的数学公式简化是类似的道理，本来一个十分复杂和冗长的计算过程，合并成一个公式后进行简化，有时候会得到一个非常简单的结果。
   • 存储优化：神经网络训练/预测过程会产生很多中间临时变量，占用大量的内存/显存空间。为节省网络的存储占用，飞桨底层采用变量存储空间复用、内存/显存垃圾及时回收等策略，保证网络以极低的内存/显存资源运行。

2. Executor创建优化后计算图或Program中的 Variable ，调度图中的Operator，从而完成模型训练/预测过程。

- IR graph：

IR全称是 Intermediate Representation，表示统一的中间表达。 IR的概念起源于编译器，是介于程序源代码与目标代码之间的中间表达形式。有如下好处：

• 便于编译优化（非必须）；
• 便于部署适配不同硬件（Nvidia GPU、Intel CPU、ARM、FPGA等），减少适配成本。

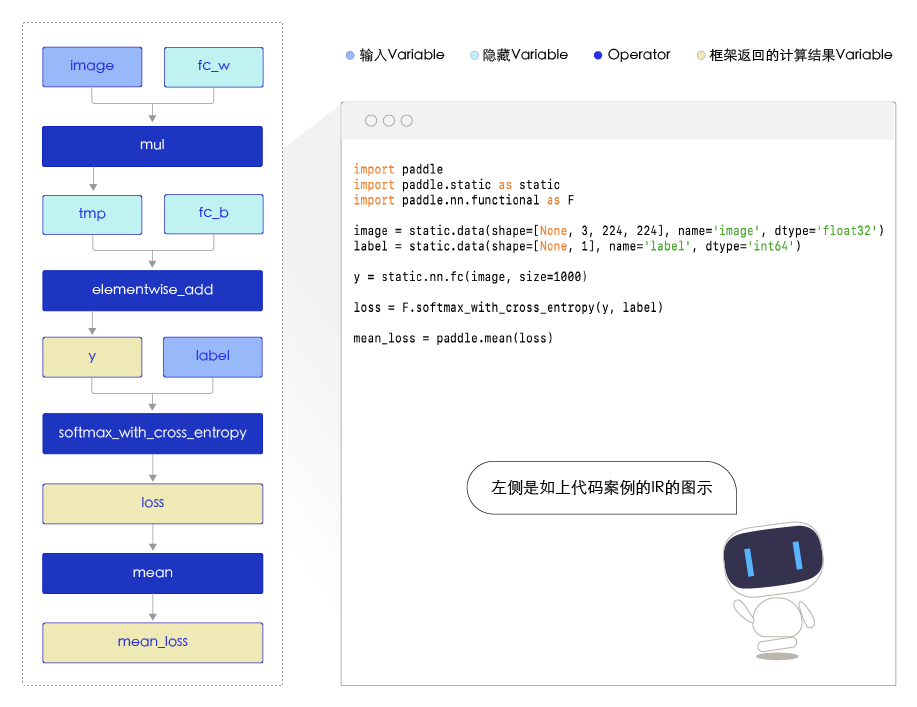
图6 IR代码图示

静态图的核心概念

飞桨静态图的核心概念如下：

• Variable：表示网络中的数据。
• Operator：表示网络中的操作。
• Block：表示编程语言中的控制流结构，如条件结构（if-else）、循环结构（while）等。
• Program：基于Protobuf的序列化能力提供模型保存、加载功能。Protobuf是Google推出的一个结构化数据的序列化框架，可将结构化数据序列化为二进制流，或从二进制流中反序列化出结构化数据。飞桨模型的保存、加载功能依托于Protobuf的序列化和反序列化能力。
• Transpiler：可选的编译步骤，作用是将一个Program转换为另一个Program。
• Intermediate Representation：在执行前期，用户定义的Program会转换为一个统一的中间表达。
• Executor：用于快速调度 Operator ，完成网络训练/预测。

飞桨动态图

在动态图模式下，Operator 是即时执行的，即用户每调用一个飞桨API，API均会马上执行返回结果。在模型训练过程中，在运行前向 Operator 的同时，框架底层会自动记录对应的反向 Operator 所需的信息，即一边执行前向网络，另一边同时构建反向计算图。

举例来说，在只有relu和reduce_sum两个算子的网络中，动态图执行流程如 图7 所示。

图7 动态图代码执行流程

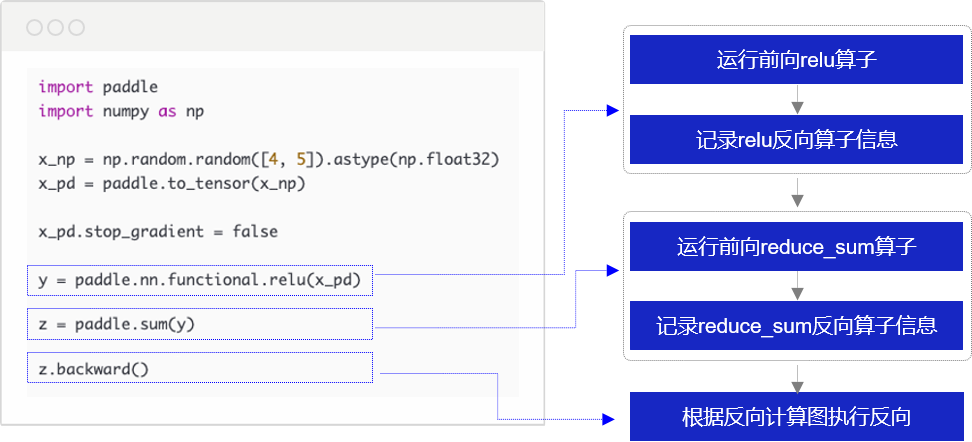
• 当用户调用 y = paddle.nn.functional.relu(x_pd) 时，框架底层会执行如下两个操作：

  • 调用relu算子，根据输入x计算输出y。
  • 记录relu反向算子需要的信息。relu算子的反向计算公式为 x_grad = y_grad * (y > 0) ，因此反向计算需要前向输出变量y，在构建反向计算图时会将y的信息记录下来。

• 当用户调用 z = paddle.sum(y) 时，框架底层会执行如下两个操作：

  • 调用reduce_sum算子，根据输入y计算出z。
  • 记录reduce_sum反向算子需要的信息。reduce_sum算子的反向计算公式为 y_grad = z_grad.broadcast(y.shape) ，因此反向计算需要前向输入变量y，在构建反向计算图时会将y的信息记录下来。

由于前向计算的同时，反向算子所需的信息已经记录下来，即反向计算图已构建完毕，因此后续用户调用 z.backward() 的时候即可根据反向计算图执行反向算子，完成网络反向计算，即依次执行：

z_grad = [1] # 反向执行的起点z_grad为[1]
y_grad = z_grad.broadcast(y.shape) # 执行reduce_sum的反向算子：y_grad为与y维度相同的Tensor，每个元素值均为1
x_grad = y_grad * (y > 0) # 执行relu的反向算子：x_grad为与y维度相同的Tensor，每个元素值为1（当y > 0时）或0（当y <= 0时）

图8 动态图根据“前向计算图”自动构建“反向计算图”

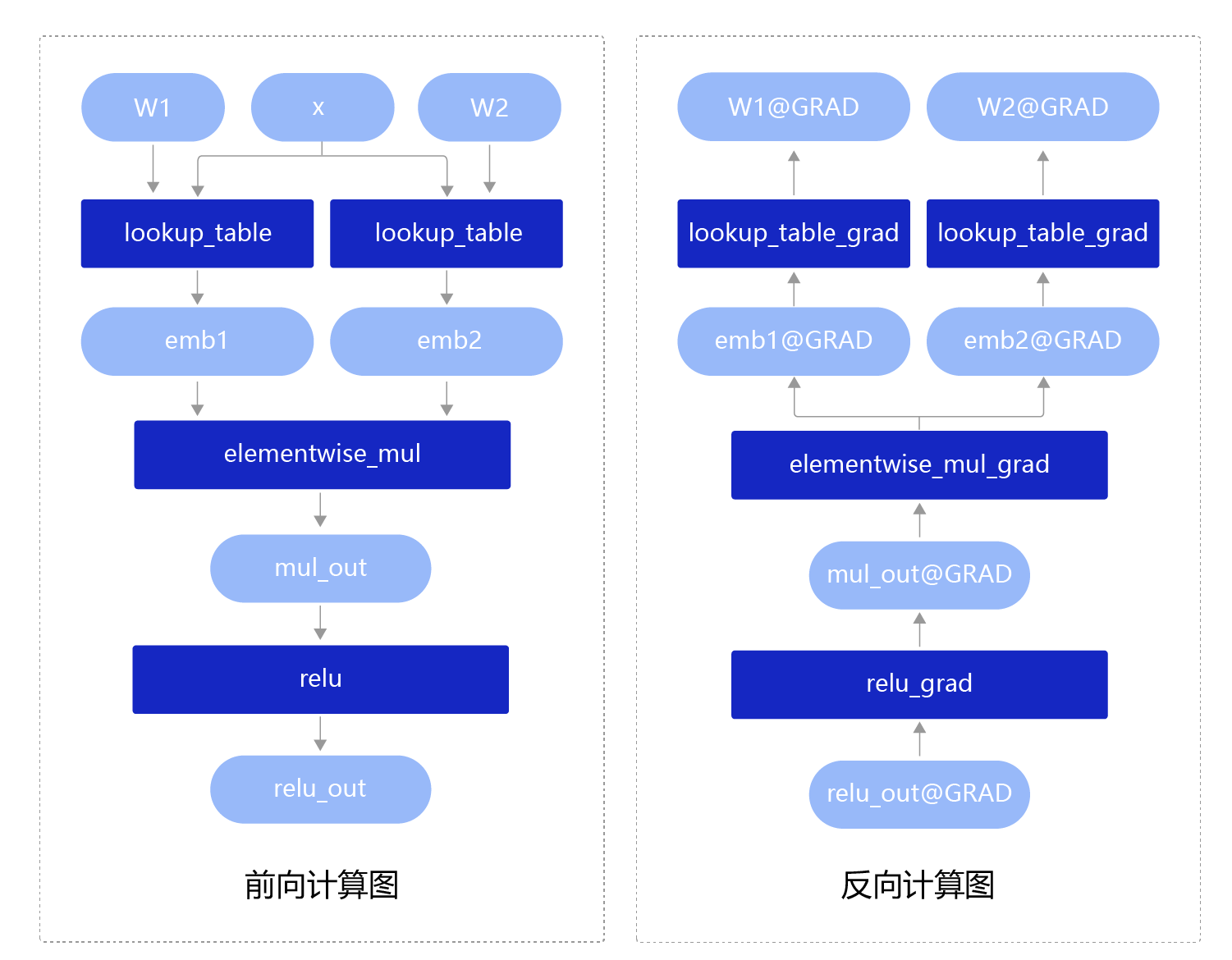
由此可见，在动态图模式下，执行器并不是先掌握完整的网络全图，再按照固定模式批量执行。而是根据Python的原生控制流代码，逐条执行前向计算过程和后向计算过程，其中后向计算的逻辑飞桨框架会在前向计算的时候自动化构建，不需要用户再操心。

动态图和静态图的差异

动态图模式和静态图模式底层算子实现的方法是相同的，不同点在于：

1. 代码组织方式不同
2. 代码执行方式不同

代码组织方式不同

在使用静态图实现算法训练时，需要使用很多代码完成预定义的过程，包括program声明，执行器Executor执行program等等。但是在动态图中，动态图的代码是实时解释执行的，训练过程也更加容易调试。

图9 动态图和静态图编码对比

• 如 图9 右侧所示，是我们相对熟悉的动态图编写模式：使用类的方式声明网络后，开启两层的训练循环，每层循环中完整的完成四个训练步骤（前向计算、计算损失，计算梯度和后向传播）。
• 但 图9 左侧则是静态图的编写模式：使用函数方式声明网络，然后要编写大量预定义的配置项，如选择的损失函数，训练所在的机器环境等等。在这些训练配置定义好后，声明一个执行器exe（运行Program，调度Operator完成网络训练/预测），将数据和模型传入exe.run()函数，一次性的完成整个训练过程。

代码执行方式不同

• 在静态图模式下，完整的网络结构在执行前是已知的，因此图优化分析的灵活性比较大，往往执行性能更佳，但调试难度大。

以算子融合Operator Fusion为例，假设网络中有3个变量x，y，z和2个算子tanh和relu。在静态图模式下，我们可以分析出变量y在后续的网络中是否还会被使用，如果不再使用y，则可以将算子tanh和relu融合为一个粗粒度的算子，消除中间变量y，以提高执行效率。

y = tanh(x)
z = relu(y)

• 在动态图模式下，完整的网络结构在执行前是未知的，因此图优化分析的灵活性比较低，执行性能往往不如静态图，但调试方便。

仍以Operator Fusion为例，因为后续网络结构未知，我们无法得知变量y在后续的网络中是否还会被使用，因此难以执行算子融合操作。但因为算子即时执行，随时均可输出网络的计算结果，更易于调试。

动转静的设计原理

在飞桨2.0版本后，动态图程序自动转成静态图训练和执行的功能已经比较成熟，简称“动转静”。这个功能有两个应用场景：

（1）因为动态图对组网中控制流的描述使用Python语言，所以静态图和动态图的模型格式不同。但部署工具使用的是静态图模型，所以动态图模型需要转成静态图才能顺利使用部署工具。

（2）静态图模式是整图优化（拿到了全部的模型组网和训练信息），在部分场景下性能更好。

“动转静”的功能较为简单，程序代码中加入一个装饰器即可，在第二章已经有专门的演示。这里展示下在飞桨2.0时代后，在用户视角的使用流程。

图10 动转静的实现方法

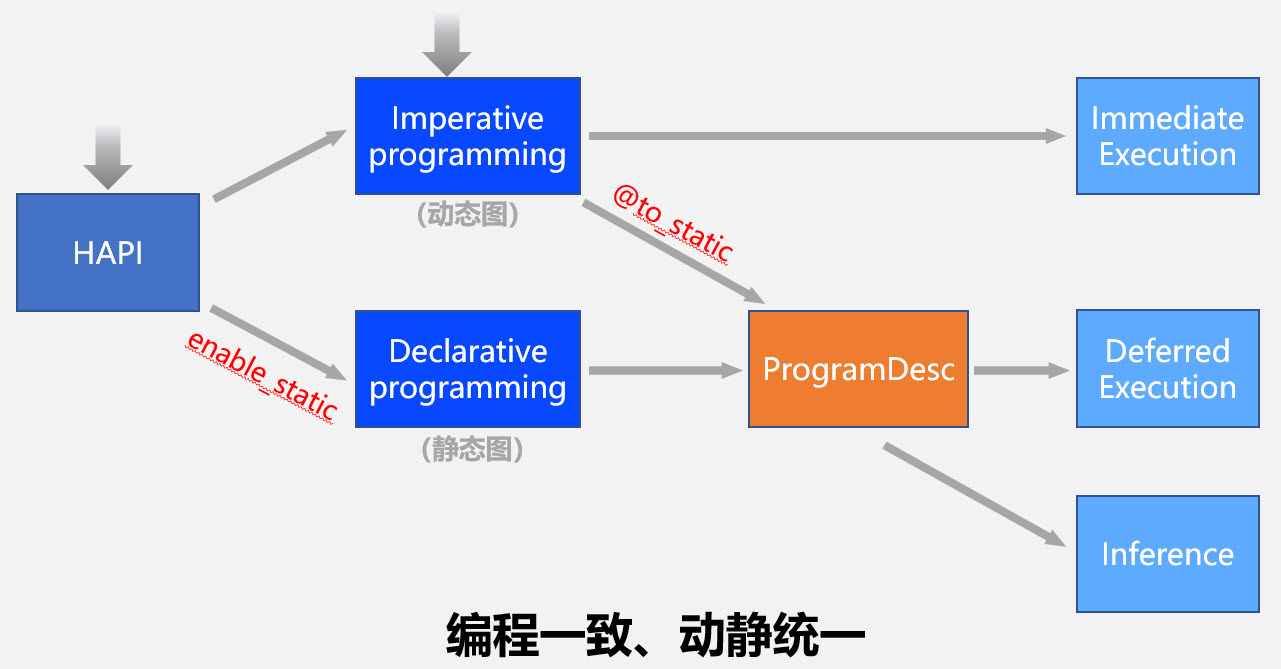
飞桨2.0默认的编程模式是动态图模式，包括使用高层API编程和基础的API编程。如果想切换到静态图模式编程，可以在程序的开始执行enable_static()函数。如果程序已经使用动态图的模式编写了，想转成静态图模式训练或者保存模型用于部署，可以使用装饰器@to_static。

飞桨前后端的整体架构

图10 飞桨内部模块的逻辑架构

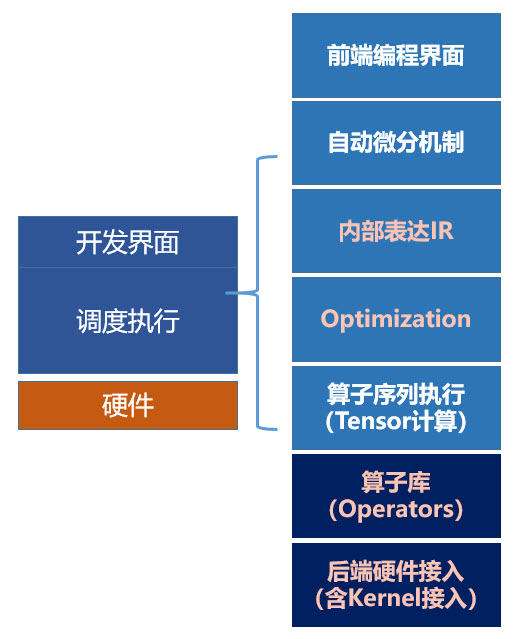
在本节内容的最后，给各位读者简单揭示下飞桨框架内部模块的逻辑结构，共有如下的7层：

1. 前端编程界面：用户使用框架的方式是基于API定义网络结构（前向计算逻辑），并控制训练过程。所以，API的设计是用户最直接感受产品是否好用的触点。
2. 自动微分机制：自动完成反向逻辑，这是深度学习框架与Numpy科学计算库的本质区别。如果只是进行数学运算，大量的科学计算库均能满足需求。深度学习框架的特色是根据用户设定的前向计算逻辑，自动生产反向计算的逻辑，使得用户不用操心模型的训练过程。
3. 内部表达IR：统一表达有两个用处，一方面便于进行算子融合等计算优化，另一方面便于序列化，用于对接不同的硬件以及进行分布式训练等，即接下来的第4步和第5步。
4. 计算图优化：可以用户手工优化，也可以框架根据策略自动优化，当然后者对用户更加友好。
5. 算子序列执行：单机单卡的训练是比较简单的，根据前向和后向计算逻辑顺序执行就好。但对于单机多卡和多机多卡的分布式训练，如何并发、异步执行计算流程，并调度异构设备等问题就需要在这个环节仔细设计。
6. 算子库：框架产品最好有完备的算子库，对于99%以上的模型均有高效实现的算子可以直接使用。但由于科学的不断前进，总有新创造的模型可能会用一些新的计算函数，所以框架要允许易添加用户自定义的算子也是同样重要的，用户添加的算子同时要具备原生算子一样的训练和推理能力，并且可以在广泛的硬件上部署。
7. 后端硬件接入：框架需要与众多种类的训练和预测硬件完成对接，这些硬件接口开放的层次往往也是不同的，典型有IR子图的高层接入方式和底层编程接口接入方式，目前最新的AI编译器技术也在尝试解决这个问题。

硬件接入方式的说明：

（1）通用编程接口（Low Level）：包括硬件厂商提供的编程语言：例如NVIDIA的CUDA、Knorons的OpenCL和寒武纪的BANG-C语言等；也包括硬件厂商提供的高性能库函数：例如NVIDIA的cuDNN、Intel的MKL和MKL-DNN等。优点是灵活，但缺点也显而易见，性能的好坏取决于负责接入框架的研发同学的能力和经验，更依赖对硬件的熟悉程度。

（2）中间表示层（Intermediate Representation，IR）接口（High Level）：组网IR和运行时API，例如NVIDIA的TensorRT、Intel的nGraph、华为HiAI IR和百度昆仑的XTCL接口。优点是屏蔽硬件细节，模型的优化、生成和执行由运行时库完成，对负责接入框架的研发同学要求较低，性能取决于硬件厂商（或IP提供商）的研发能力，相对可控。

除了前端编程界面和后端硬件接入之外，中间的四个步骤属于框架内部的调度执行模块。好的框架要求前端的编程界面要易于理解和使用（包括调试），目前看起来动态图的执行模式是广泛被认可的。好的框架要求计算调度的性能要高，目前飞桨在这方面做了相当多的优化，从AI-Rank的榜单来看，飞桨在多数模型的多数硬件上取得了领先的速度。最后，好的框架要求能够快速的对接各种新型硬件，并具备较好的计算性能。这方面飞桨不仅仅靠自己的部署产品，还与广泛的硬件厂商和Onnx联盟达成合作。