混合精度推理

混合精度推理是通过混合使用单精度（FP32）和半精度（FP16）来加速神经网络推理过程。相较于使用单精度（FP32）进行推理，既能能减少内存/显存占用，推理更大的网络，又能降低显存访问和计算耗时开销，在保证模型推理精度持平的情形下，提升推理效率。

一、半精度浮点类型 FP16

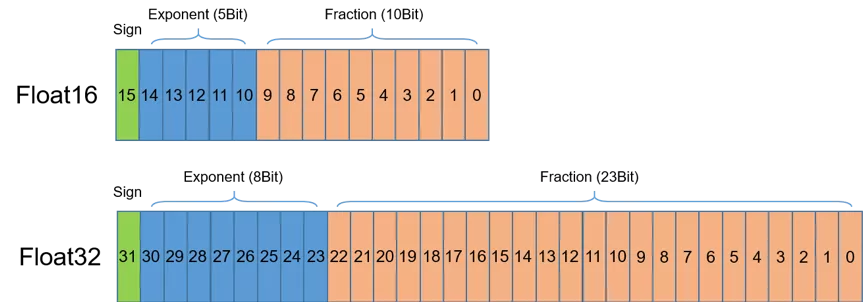
首先介绍半精度（FP16）。如图1所示，半精度（FP16）是一种相对较新的浮点类型，在计算机中使用2字节（16位）存储。在IEEE 754-2008标准中，它亦被称作binary16。与计算中常用的单精度（FP32）和双精度（FP64）类型相比，FP16更适于在精度要求不高的场景中使用。

missing
图 1. 半精度和单精度数据示意图

二、NVIDIA GPU的FP16算力

混合精度推理使用半精度浮点（FP16）和单精度（FP32）浮点即可达到与使用纯单精度推理相同的准确率，并可加速模型的推理速度，这主要得益于英伟达从Volta架构开始推出的Tensor Core技术。在使用FP16计算时具有如下特点：

  • FP16可降低一半的内存带宽和存储需求，这使得在相同的硬件条件下研究人员可使用更大更复杂的模型以及更大的batch size大小。

  • FP16可以充分利用英伟达Volta、Turing、Ampere架构GPU提供的Tensor Cores技术。在相同的GPU硬件上，Tensor Cores的FP16计算吞吐量是FP32的8倍。

三、Paddle-GPU 混合精度推理

本节主要介绍 GPU 原生混合精度推理流程，有两种方式：一阶段式和二阶段式。一阶段式直接输入 FP32 的模型，给 FP16 或 FP32 的数据，通过配置 Config 来指定推理精度。二阶段式主要分为模型精度转换和模型推理两个步骤。

3.1 一阶段式

只需一行代码。

// cpp 示例
config.EnableUseGpu(512, 0, Precision::kHalf);

# python 示例
config.enable_use_gpu(512, 0, PrecisionType.Half)

3.2 二阶段式

3.2.1 模型精度转换

convert_to_mixed_precision接口可对模型精度格式进行修改，可使用以下 python 脚本进行模型精度转换。

from paddle.inference import PrecisionType, PlaceType
from paddle.inference import convert_to_mixed_precision
import argparse

if __name__ == "__main__":
    parser = argparse.ArgumentParser()
    parser.add_argument('src_model', type=str, help='src_model')
    parser.add_argument('src_params', type=str, help='src_params')
    parser.add_argument('dst_model', type=str, help='dst_model')
    parser.add_argument('dst_params', type=str, help='dst_params')
    args = parser.parse_args()
    black_list = set()

    convert_to_mixed_precision(
        args.src_model,     # fp32模型文件路径
        args.src_params,    # fp32权重文件路径
        args.dst_model,     # 混合精度模型文件保存路径
        args.dst_params,    # 混合精度权重文件保存路径
        PrecisionType.Half, # 转换精度，如 PrecisionType.Half
        PlaceType.GPU,      # 后端，如 PlaceType.GPU
        True,               # 保留输入输出精度信息，若为 True 则输入输出保留为 fp32 类型，否则转为 precision 类型
        black_list          # 黑名单列表，哪些 op 不需要进行精度类型转换
    )

实现思想基本可描述为：对模型进行拓扑遍历，依次检查算子在 backend 后端上是否支持 precision 精度类型，如果支持，则我们将该算子标记为混合精度类型，并且设置其输入输出均为 precision 类型，当算子输入与期望输入类型不符时，插入 cast 算子进行精度转换。

3.2.2 模型推理

得到混合精度模型后，可按照正常的推理逻辑进行推理，详情请参考 GPU 原生推理。

四、混合精度推理性能优化

Paddle Inference 混合精度推理性能的根本原因是：利用 Tensor Core 来加速 FP16 下的matmul和conv运算，为了获得最佳的加速效果，Tensor Core 对矩阵乘和卷积运算有一定的使用约束，约束如下：

4.1 矩阵乘使用建议

通用矩阵乘 (GEMM) 定义为：C = A * B + C，其中：

  • A 维度为：M x K

  • B 维度为：K x N

  • C 维度为：M x N

矩阵乘使用建议如下：

  • 根据Tensor Core使用建议，当矩阵维数 M、N、K 是8（A100架构GPU为16）的倍数时（FP16数据下），性能最优。

4.2 卷积计算使用建议

卷积计算定义为：NKPQ = NCHW * KCRS，其中：

  • N 代表：batch size

  • K 代表：输出数据的通道数

  • P 代表：输出数据的高度

  • Q 代表：输出数据的宽度

  • C 代表：输入数据的通道数

  • H 代表：输入数据的高度

  • W 代表：输入数据的宽度

  • R 代表：滤波器的高度

  • S 代表：滤波器的宽度

卷积计算使用建议如下：

  • 输入/输出数据的通道数（C/K）可以被8整除（FP16），（cudnn7.6.3及以上的版本，如果不是8的倍数将会被自动填充）

  • 对于网络第一层，通道数设置为4可以获得最佳的运算性能（NVIDIA为网络的第一层卷积提供了特殊实现，使用4通道性能更优）

  • 设置内存中的张量布局为NHWC格式（如果输入NCHW格式，Tesor Core会自动转换为NHWC，当输入输出数值较大的时候，这种转置的开销往往更大）