开发 C++ 算子¶
新增飞桨 API 主要包含两种情况:
不需要开发新的 C++ 算子,可以用其他 Python API 组合得到新的 API,只写 Python 代码即可。
需要开发新的 C++ 算子,需要用 C++ 开发算子实现代码、再封装 Python API 代码。
针对第二种情况,可参考本文完成 C++ 算子的开发,并参考 开发 API Python 端 章节完成 Python 端的开发。
注:飞桨 C++ 算子的开发范式正处在重构升级后的上线初期,如果在开发过程中遇到问题欢迎通过 Issue 向我们反馈。
一、开发前准备¶
开发代码前请确认:
已根据 API 设计和命名规范 确定了新增 API 的名称和存放位置;
已提交 API 设计文档 并通过评审;
已将 PaddlePaddle/Paddle 仓库的代码获取到本地,准备好了 Paddle 开发环境。
二、开发流程介绍¶
新增一个 C++ 算子大概需要以下几个步骤:
新增算子描述及定义:描述前反向算子的输入、输出、属性,实现 InferMeta 函数;
新增算子 Kernel:实现算子在各种设备上的计算逻辑;
封装 Python API:封装 Python 端调用算子的接口;
添加单元测试:验证新增算子的正确性。
以上步骤需要添加的文件,在 PaddlePaddle/Paddle 中的位置如下表所示(假设算子名为xxx):
| 内容 | 新增文件位置 |
|---|---|
| 算子描述及定义 | 前向算子定义:paddle/phi/api/yaml/ops.yaml 反向算子定义:paddle/phi/api/yaml/backward.yaml |
| 算子 InferMeta | paddle/phi/infermeta 目录下的相应文件中 |
| 算子 Kernel | paddle/phi/kernels 目录下的如下文件:(一般情况) xxx_kernel.h xxx_kernel.cc xxx_grad_kernel.h xxx_grad_kernel.cc |
| Python API | python/paddle 目录下的相应子目录中的 .py 文件,遵循相似功能的 API 放在同一文件夹的原则 |
| 单元测试 | python/paddle/fluid/tests/unittests 目录下的相应文件中: test_xxx_op.py |
用户使用飞桨开发神经网络模型时使用的 Python 接口(如 paddle.add(), paddle.relu()等) 我们一般称都为飞桨的 Python API,每个运算类的 Python API 在框架内部都会对应到一个或者多个 C++ 端算子,每个算子在不同硬件设备上(CPU, GPU 等)实现的运算逻辑代码又被称为 Kernel, 这里主要是由于不同硬件设备提供的编程接口不同,所以虽然同一个算子的不同硬件设备 Kernel 都实现了相同的数学运算逻辑,但在代码实现上却有所差异。算子 InferMeta 函数是在算子 kernel 执行前先将输出结果的维度、数据类型等信息进行处理,由于计算量较小所以可以直接在 CPU 上计算,因此每个算子只需要实现一个 InferMeta 函数,而不必像 Kernel 一样在不同硬件上实现多个。
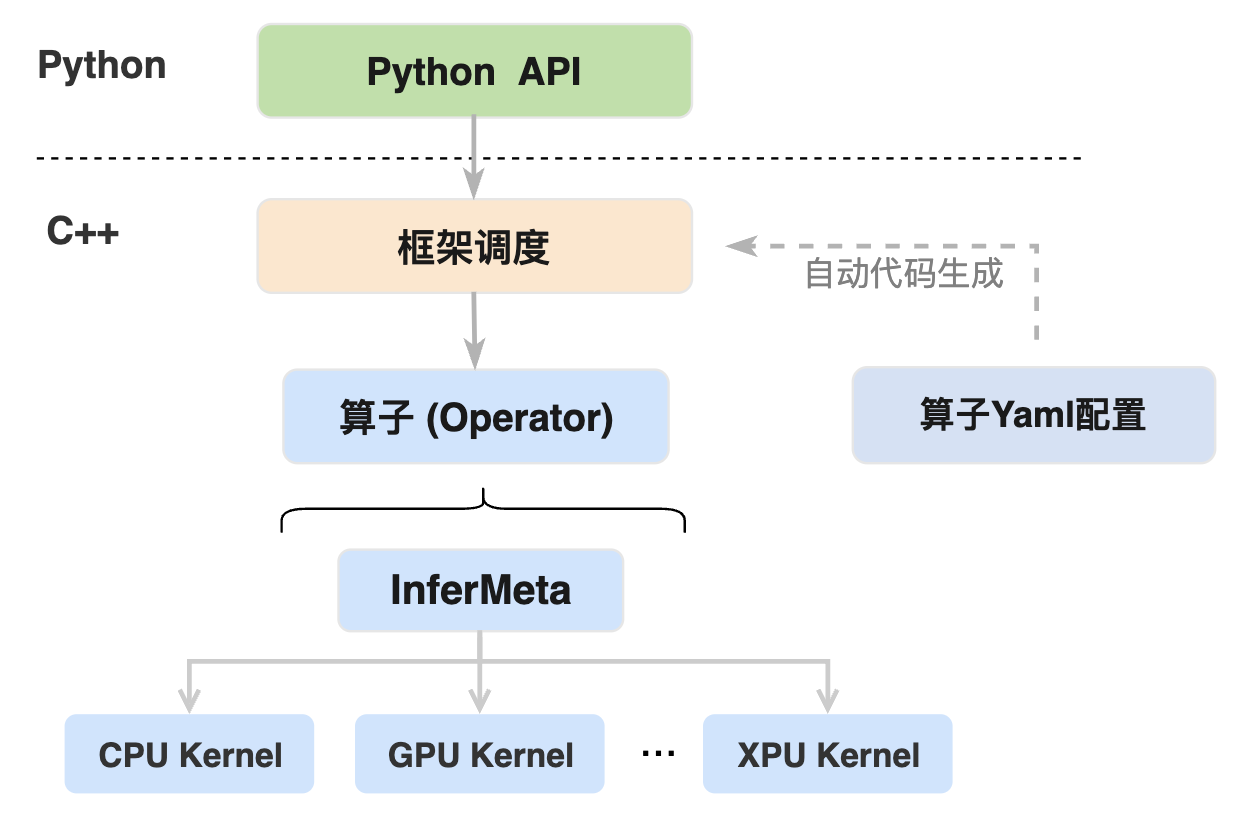
Python API、算子 Yaml 配置、算子 InferMeta 函数 和算子 Kernel 之间的关系如上图所示,最上层为用户使用的飞桨 Python API 接口,Python API 执行时会进入到 C++ 端由框架进行调度并执行相应的算子逻辑,算子的执行主要包括两个过程:
(1)执行算子 InferMeta 函数完成输出结果的维度、数据类型等静态信息的推导。
(2)根据输入变量的设备信息选择对应的硬件设备来执行算子 Kernel,完成输出结果的数值计算。
Python API 到算子 InferMeta 函数和 Kernel 调用之间的框架调度部分的逻辑代码主要通过算子 Yaml 配置中的信息自动生成,也可以理解为算子 Yaml 配置的作用是通过自动代码生成将上层 Python API 与底层算子的 Kernel 建立连接。
接下来以 trace 算子操作,计算输入 Tensor 在指定平面上的对角线元素之和,并输出相应的计算结果,即以 paddle.trace 为例来介绍如何新增算子。
| 内容 | trace 示例代码仓库链接 |
|---|---|
| 算子描述及定义 | paddle/phi/api/yaml/ops.yaml paddle/phi/api/yaml/backward.yaml |
| 算子 InferMeta | paddle/phi/infermeta/unary.cc |
| 算子 Kernel | paddle/phi/kernels 目录下的如下文件: /trace_kernel.h /cpu/trace_kernel.cc /gpu/trace_kernel.cu /trace_grad_kernel.h /cpu/trace_grad_kernel.cc /gpu/trace_grad_kernel.cu |
| Python API | python/paddle/tensor/math.py |
| 单元测试 | python/paddle/fluid/tests/unittests/test_trace_op.py |
三、新增算子描述及定义¶
算子描述及定义主要是定义算子的基本属性,包括算子的输入、输出以及各项非计算逻辑的配置,这些都是设备无关的。
3.1 算子 Yaml 文件配置¶
在 paddle/phi/api/yaml/ops.yaml 和 paddle/phi/api/yaml/backward.yaml 文件中对算子进行描述及定义,在框架编译时会根据 YAML 文件中的配置自动生成 C++ 端的相关代码接口以及内部实现(详见下文 8.1 Paddle 基于 Yaml 配置自动生成算子代码的逻辑解读 小节的介绍),下面主要以 paddle.trace 为例介绍算子的 Yaml 配置规则:
paddle/phi/api/yaml/ops.yaml 中 trace 相关配置:
- op : trace
args : (Tensor x, int offset = 0, int axis1 = 0, int axis2 = 1)
output : Tensor(out)
infer_meta :
func : TraceInferMeta
kernel :
func : trace
backward : trace_grad
paddle/phi/api/yaml/backward.yaml 中 trace 相关配置:
- backward_op : trace_grad
forward : trace (Tensor x, int offset, int axis1, int axis2) -> Tensor(out)
args : (Tensor x, Tensor out_grad, int offset, int axis1, int axis2)
output : Tensor(x_grad)
infer_meta :
func : UnchangedInferMeta
param : [x]
kernel :
func : trace_grad
data_type : x
no_need_buffer : x
ops.yaml 和 backward.yaml 分别对算子的前向和反向进行配置,首先 ops.yaml 中前向算子的配置规则如下:
| 配置项 | 配置内容及规则 |
|---|---|
| api | 算子名称,与该算子 Python API 函数名相同(命名方式为:全小写+下划线),示例中为 trace |
| args | 算子输入参数,与该算子 Python API 函数的输入参数对应(当前支持的输入数据类型包括:Tensor, Tensor[], float, double, bool, int, int64_t, int[], int64_t[], str, Place, DataType, DataLayout, IntArray, Scalar)。我们一般称这里 Tensor 类型的参数为 Input(输入),非 Tensor 类型的参数为 Attribute(属性) 注:Tensor[]表示 Tensor 数组;IntArray 为 int 类型数组,主要用于表示 shape,index 和 axes 等类型数据,可以直接使用 Tensor 或者普通整型数组构造,目前仍在测试阶段,如非必要暂不建议使用;Scalar 表示标量,可以支持不同的普通数据类型 |
| output | 算子输出类型(目前支持 Tensor 和 Tensor[]类型),多个输出间用逗号“,”分隔开。可以使用”()”选择性标记输入的名字,如未标记默认为'out' 注:当返回类型为 Tensor[]时,由于数组的 size 要在 kernel 执行前推导完成,所以需要在 Tensor[]后的'{}'内通过表达式指定返回数组的 size,如:Tensor[](out){input.size()} |
| infer_meta | InferMeta 函数负责根据输入变量推断返回 Tensor 的维度与类型,这里是对算子使用的 InferMeta 函数进行配置 |
| infer_meta:func | 调用的 InferMeta 函数,这里 trace 调用的是 TraceInferMeta 函数 |
| infer_meta:param | InferMeta 函数的输入参数,可以对 args 中的参数进行选择传入,未配置则默认传入 args 中的所有参数。示例中未配置本项,所以传入的参数为[x, offset, axis1, axis2]。output 项中的参数作为输出无需配置会自动传入 InferMeta 函数中 |
| kernel | 算子的计算 Kernel 配置 |
| kernel:func | 算子对应 kernel 函数的注册名 |
| kernel:param | kernel 函数的输入参数,配置规则与 InferMeta 函数的 param 配置项相同 |
| kernel:data_type | 根据指定参数推导调用 kernel 的 data_type(对应 kernel 函数的模板参数'T'),默认不进行配置,会根据输入 Tensor 自动进行推导。如果 kernel 的 data_type 类型由某个输入参数(Tensor 或者 DataType 参数),需要将该参数的变量名填入该项。示例中未配置则 kernel 的 data_type 由输入变量'x'决定 |
| kernel:backend | 根据指定参数来选择调用 kernel 的 Backend(Kernel 执行的具体设备,如 CPU、GPU 等),默认不进行配置,会根据输入 Tensor 自动进行推导。如果 kernel 执行的 backend 类型由某个输入参数(Tensor 或者 Backend 参数)决定,需要将该参数的变量名填入该项。示例中未配置则 kernel 执行的 Backend 与输入变量'x'的 Backend 相同 |
| backward | 算子对应的反向算子名称,如果没有反向则不需要配置,示例中 trace 算子的反向为 trace_grad |
| 特殊配置项(目前特殊配置项还处于不稳定阶段,后续可能会有调整更新) | |
| optional | 指定输入 Tensor 为可选输入,用法可参考 dropout 中 seed_tensor(python/paddle/utils/code_gen/legacy_ops.yaml 中) |
| inplace | 算子对指定的输入做原位处理并作为输出结果返回,使用格式:(x -> out),具体用法可参考 relu 算子 特殊规则:如果 api 中算子名称有'_'后缀则只生成支持 inplace 功能的接口,如果算子名称没有'_'后缀,则会同时生成支持 inplace 操作的接口(自动添加'_'后缀)和不支持 inplace 的普通接口共两套接口 |
| view | 与 inplace 机制类似,区别在于 view 模式返回的结果只是与输入共享内存,并不是输入 Tensor 变量本身,使用格式:(x -> out),具体用法可参考 reshape 算子 |
| intermediate | 标记前向计算中输出的用于反向计算的中间变量,不会出现在 Python API 的返回结果中,相关设计正在完善中,新增算子时不建议使用 |
| invoke | 复用已有的算子接口或实现自定义的 C++ API,配置时以函数调用的形式配置即可,使用 invoke 时则不需要配置 infer_meta 和 kernel。 a. 如果是复用已有算子,需要被复用的算子为前向算子且两者的返回值类型相同,可参考 zeros_like 算子 b. 如果是实现自定义的 C++ API,需要在'paddle/phi/api/lib/api_custom_impl.h'声明自定义实现函数并在'paddle/phi/api/lib/api_custom_impl.cc'中进行实现,具体可参考 embedding 算子 |
| 配置项 | 配置内容及规则 |
|---|---|
| backward_op | 反向算子名称,一般命名方式为:前向算子名称+'_grad',二阶算子则为前向算子名称+'_double_grad' |
| forward | 对应前向算子的名称、参数、返回值,需要与 ops.yaml 中前向算子配置一致 |
| args | 反向算子输入参数, 示例中'x'表示将前向的'x'变量输入到反向,'out_grad'表示前向输出'out'对应的反向梯度 约束条件 1:所有参数需要在 forward 配置项的参数中(输入、输出以及输出对应的反向梯度)找到对应(根据变量名匹配) 约束条件 2:反向输入参数需要以:a.前向输入 Tensor b.前向输出 Tensor c.前向输出 Tensor 的反向梯度 d.前向非 Tensor 类型属性变量(Attribute) 的顺序排列,反向计算中不需要使用的前向变量无须添加 |
| output | 反向算子输出,顺序需要与前向输入 Tensor 一致,比如前向输入(Tensor x, Tensor y),则反向输出必须为 Tensor(x_grad), Tensor(y_grad) |
| infer_meta | 与前向配置规则相同 |
| kernel | 与前向配置规则相同 |
| backward | 反向算子对应的更高阶反向算子名称,如一阶反向算子的反向为二阶反向算子 |
| 特殊配置项(目前特殊配置项还处于不稳定阶段,后续可能会有调整更新) | |
| no_need_buffer | 可选配置,标记的 Tensor 变量在前向运行完成后,持有的内存或显存会被释放,以减少训练过程中的内存使用。trace_grad 由于反向算子只需要前向变量'x'的维度信息,不需要内存数据,所以可以标记为 no_need_buffer 提前释放内存 注意:由于 Tensor 内存被释放后会影响 dtype 接口的使用,所以需要在 kernel 的 data_type 配置项中指定其他的 Tensor 来推导 kernel 的 data_type |
| optional | 与前向配置规则相同 |
| inplace | 与前向配置规则相同 |
3.2 实现 InferMeta 函数¶
InferMeta 函数是根据输入参数,推断算子输出 Tensor 基本信息的函数,推断的信息包括输出 Tensor 的 shape、data type,同时它也承担了检查输入数据维度、类型等是否合法的功能。
说明:InferMeta 与 kernel 共同组成了一个算子的运算过程。InferMeta 在 kernel 前执行,用于维度、数据类型等信息的计算处理,这些信息在没有具体数据时依然可以通过输入参数完成输出结果的信息推导(例如两个维度为 2x3 的张量相加,输出结果的维度也一定是 2x3),可以利用这些信息优化训练过程中资源的分配和使用,kernel 中也不再需要专门推导这些信息。kernel 则用于具体数据的逻辑计算,为 InferMeta 函数推导得到的张量填充具体的结果值。
trace 算子的 InferMeta 函数 实现如下:
void TraceInferMeta(
const MetaTensor& x, int offset, int axis1, int axis2, MetaTensor* out) {
int dim1 = axis1;
int dim2 = axis2;
auto x_dims = x.dims();
int dim1_ = dim1 < 0 ? x_dims.size() + dim1 : dim1;
int dim2_ = dim2 < 0 ? x_dims.size() + dim2 : dim2;
PADDLE_ENFORCE_GE(
x_dims.size(),
2,
phi::errors::OutOfRange(
"Input's dim is out of range (expected at least 2, but got %ld).",
x_dims.size()));
PADDLE_ENFORCE_LT(
dim1_,
x_dims.size(),
phi::errors::OutOfRange(
"Attr(dim1) is out of range (expected to be in range of [%ld, "
"%ld], but got %ld).",
-(x_dims.size()),
(x_dims.size() - 1),
dim1));
PADDLE_ENFORCE_LT(
dim2_,
x_dims.size(),
phi::errors::OutOfRange(
"Attr(dim2) is out of range (expected to be in range of [%ld, "
"%ld], but got %ld).",
-(x_dims.size()),
(x_dims.size() - 1),
dim2));
PADDLE_ENFORCE_NE(
dim1_,
dim2_,
phi::errors::InvalidArgument("The dimensions should not be identical "
"%ld vs %ld.",
dim1,
dim2));
auto sizes = vectorize(x_dims);
if (x_dims.size() == 2) {
sizes.clear();
sizes.push_back(1);
} else {
sizes.erase(sizes.begin() + std::max(dim1_, dim2_));
sizes.erase(sizes.begin() + std::min(dim1_, dim2_));
}
out->set_dims(phi::make_ddim(sizes));
out->set_dtype(x.dtype());
}
其中,MetaTensor是对底层异构 Tensor 的抽象封装,仅支持对底层 Tensor 的维度、数据类型、布局等属性进行读取和设置,具体方法请参考 meta_tensor.h。
InferMeta 的实现位置
InferMeta 的文件放置规则(paddle/phi/infermeta 目录下,以 Tensor 输入个数为判定标准):
nullary.h:没有输入 Tensor 参数的函数unary.h:仅有一个输入 Tensor 参数的函数binary.h:有两个输入 Tensor 参数的函数ternary.h:有三个输入 Tensor 参数的函数multiary.h:有三个以上输入 Tensor 或者输入为vector<Tensor>的函数backward.h:反向算子的 InferMeta 函数一律在此文件中,不受前序规则限制
InferMeta 的编译时与运行时
在静态图模型中,InferMeta操作在 编译时(compile time)和运行时(run time) 都会被调用,在 compile time 时,由于真实的维度未知,框架内部用 -1 来表示,在 run time 时,用实际的维度表示,因此维度的值在 compile time 和 run time 时可能不一致,如果存在维度的判断和运算操作,InferMeta 就需要区分 compile time 和 run time。
对于此类 InferMeta 函数,需要在 InferMeta 函数声明的参数列表末尾增加 MetaConfig 参数,例如:
void ConcatInferMeta(const std::vector<MetaTensor*>& x,
const Scalar& axis_scalar,
MetaTensor* out,
MetaConfig config = MetaConfig());
然后在函数体中,使用 config.is_runtime 判断处于编译时还是运行时。
具体地,以下两种情况(检查、运算)需要区分 compile time 和 run time。
检查:
如以下代码:
int i = xxx;
PADDLE_ENFORCE_GT(x.dims()[i] , 10)
在 compile time 的时候,x.dims()[i] 可能等于 -1,导致这个 PADDLE_ENFORCE_GT 报错退出。
如果用了以下 paddle 中定义的宏进行判断,都需要注意区分 compile time 和 run time。
PADDLE_ENFORCE_EQ (x.dims()[i] , 10)
PADDLE_ENFORCE_NE (x.dims()[i] , 10)
PADDLE_ENFORCE_GT (x.dims()[i] , 10)
PADDLE_ENFORCE_GE (x.dims()[i] , 10)
PADDLE_ENFORCE_LT (x.dims()[i] , 10)
PADDLE_ENFORCE_LE (x.dims()[i] , 10)
运算:
如以下代码:
auto x_dim = x.dims();
int i = xxx;
y_dim[0] = x_dim[i] + 10
在 compile time 的时候,x_dim[i] 可能等于 -1,得到的 y_dim[0] 等于 9,是不符合逻辑的。
如果用到了类似以下的运算操作,都需要区分 compile time 和 run time:
y_dim[i] = x_dim[i] + 10
y_dim[i] = x_dim[i] - 10
y_dim[i] = x_dim[i] * 10
y_dim[i] = x_dim[i] / 10
y_dim[i] = x_dim[i] + z_dim[i]
处理的标准:
检查: compile time 的时候不判断维度等于 -1 的情况,但在 runtime 的时候检查
运算: -1 和其他数做任何运算都要等于 -1
参考代码:
判断的实现方法可以参考 SigmoidCrossEntropyWithLogitsInferMeta,SigmoidCrossEntropyWithLogits 要求 X 和 labels 的两个输入,除了最后一维以外,其他的维度完全一致。
bool check = true;
if ((!config.is_runtime) &&
(phi::product(x_dims) <= 0 || phi::product(labels_dims) <= 0)) {
check = false;
}
if (check) {
PADDLE_ENFORCE_EQ(
phi::slice_ddim(x_dims, 0, rank),
phi::slice_ddim(labels_dims, 0, rank),
phi::errors::InvalidArgument(
"Input(X) and Input(Label) shall have the same shape "
"except the last dimension. But received: the shape of "
"Input(X) is [%s], the shape of Input(Label) is [%s].",
x_dims,
labels_dims));
}
运算的实现可以参考 ConcatInferMeta,concat 在 InferShape 判断时,调用
ComputeAndCheckShape,除了进行 concat 轴之外,其他的维度完全一致;在生成 output 的维度时,把 concat 轴的维度求和,其他的维度和输入保持一致。
const size_t n = inputs_dims.size();
auto out_dims = inputs_dims[0];
size_t in_zero_dims_size = out_dims.size();
for (size_t i = 1; i < n; i++) {
PADDLE_ENFORCE_EQ(
inputs_dims[i].size(),
out_dims.size(),
phi::errors::InvalidArgument("The shape of input[0] and input[%d] "
"is expected to be equal."
"But received input[0]'s shape = "
"[%s], input[%d]'s shape = [%s].",
i,
inputs_dims[0],
i,
inputs_dims[i]));
for (size_t j = 0; j < in_zero_dims_size; j++) {
if (j == axis) {
if (is_runtime) {
out_dims[axis] += inputs_dims[i][j];
} else {
if (inputs_dims[i][j] == -1 || out_dims[j] == -1) {
out_dims[axis] = -1;
} else {
out_dims[axis] += inputs_dims[i][j];
}
}
} else {
bool check_shape =
is_runtime || (inputs_dims[0][j] > 0 && inputs_dims[i][j] > 0);
if (check_shape) {
// check all shape in run time
PADDLE_ENFORCE_EQ(inputs_dims[0][j],
inputs_dims[i][j],
phi::errors::InvalidArgument(
"The %d-th dimension of input[0] and input[%d] "
"is expected to be equal."
"But received input[0]'s shape = "
"[%s], input[%d]'s shape = [%s].",
j,
i,
inputs_dims[0],
i,
inputs_dims[i]));
}
if (!is_runtime && out_dims[j] == -1 && inputs_dims[i][j] > 0) {
out_dims[j] = inputs_dims[i][j];
}
}
}
}
四、新增算子 Kernel¶
4.1 Kernels 目录结构¶
新增算子 Kernel 在 paddle/phi/kernels 目录中完成,基本目录结构如下:
paddle/phi/kernels
./ (根目录放置设备无关的 kernel 声明和实现)
./cpu(仅放置 cpu 后端的 kernel 实现)
./gpu(仅放置 gpu 后端的 kernel 实现)
./xpu(仅放置百度 kunlun 后端的 kernel 实现)
./gpudnn
./funcs(放置一些支持多设备的、在多个 kernel 中使用的公共 functor 和 functions)
...
一般情况下,新增算子仅需要关注 kernels 根目录及 kernel 所支持设备的子目录即可:
kernels 根目录,放置设备无关的 kernel.h 和 kernel.cc
例如,一个 kernel 除了一些简单的设备无关的 C++ 逻辑,关键计算逻辑均是复用已有的 kernel 函数实现的,那么这个 kernel 实现是天然能够适配所有设备及后端的,所以它的声明和实现均直接放置到 kernels 目录下即可。
kernels 下一级子目录,原则上按照后端分类按需新建,放置特定后端的 kernel 实现代码。
下面给出两种典型 kernel 新增时文件放置位置的说明(假设算子名为xxx):
新增与设备无关的 kernel
该类 kernel 实现与所有硬件设备无关,只需要一份代码实现,可参考 reshape kernel。其新增文件及目录包括:
paddle/phi/kernels/xxx_kernel.hpaddle/phi/kernels/xxx_kernel.cc
如果是反向 kernel,则使用
grad_kernel后缀即可:paddle/phi/kernels/xxx_grad_kernel.hpaddle/phi/kernels/xxx_grad_kernel.cc
新增与设备相关、且 CPU & GPU 分别实现的 kernel
还有部分 kernel 的实现,CPU 和 GPU 上逻辑不同,此时没有共同实现的代码,需要区分 CPU 和 GPU 硬件。 CPU 的实现位于
paddle/phi/kernels/cpu目录下; GPU 的实现位于paddle/phi/kernels/gpu下,可参考 dot kernel,cast kernel 等。其新增文件及目录包括:paddle/phi/kernels/xxx_kernel.hpaddle/phi/kernels/cpu/xxx_kernel.ccpaddle/phi/kernels/gpu/xxx_kernel.cu相应地,反向 kernel 新增文件为:
paddle/phi/kernels/xxx_grad_kernel.hpaddle/phi/kernels/cpu/xxx_grad_kernel.ccpaddle/phi/kernels/gpu/xxx_grad_kernel.cu
4.2 Kernel 写法¶
4.2.1 声明 Kernel 函数¶
以 trace 算子为例,首先在paddle/phi/kernels目录下新建 trace_kernel.h 文件,用于放置前向 kernel 函数声明。
注意:
Kernel 函数声明的参数列表原则上与 Python API 参数列表一致;
所有的 kernel 声明,统一放在 namespace phi 中,缩短函数的调用前缀使调用写法更加简洁。
namespace phi {
template <typename T, typename Context>
void TraceKernel(const Context& dev_ctx,
const DenseTensor& x,
int offset,
int axis1,
int axis2,
DenseTensor* out);
}
模板为固定写法,说明如下:
第一个模板参数为数据类型
T,第二个模板参数为设备上下文Context,template <typename T, typename Context>函数命名:kernel 的命名统一加 kernel 后缀。即:kernel 名称 + kernel 后缀,驼峰式命名,例如:AddKernel
参数顺序:Context, InputTensor …, Attribute …, OutTensor* 。即:第一位参数为 Context, 后边为输入的 Tensor, 接着是输入的属性参数, 最后是输出的 Tensor 的指针参数。如果 kernel 没有输入 Tensor 或者没有属性参数,略过即可
第 1 个函数参数,类型为
const Context&的 dev_ctx第 2 个函数参数,输入 Tensor,类型一般为
const DenseTensor&第 3-5 个函数参数,均为 attribute(根据具体的含义,选择特定的 int,float,vector 等类型),多个 attribute 可以参考 Python 端 API 定义的顺序,变量命名对齐 Python API
第 6 个函数参数,输出 Tensor,类型一般为
DenseTensor*,多个 output 可以参考 python 端 API 定义的顺序, 变量命名对齐 python api
特殊情况说明:
特殊模板参数:对于某些 kernel (如 reshape ,copy),这些 kernel 不关注数据类型 T, 可以省去第一个模板参数,即为:
template <typename Context>特殊输入类型:对于某些特殊 kernel (如 concat 和 split kernel)的部分输入或输出是数组类型的 DenseTensor, 此时输入类型为:
const std::vector<const DenseTensor*>&; 输出类型为:std::vector<DenseTensor*>
4.2.2 实现 Kernel 函数¶
(1)复用已有 Kernel 实现设备无关 Kernel 函数
由于目前的 kernel 复用机制为新推出的功能,暂未对已有算子进行升级改造,所以这里我们以一个不在框架中的 linear 算子 (out = x * w + b) 为例来介绍复用已有 kernel 实现设备无关 Kernel 函数的方法。(linear kernel 的实现源码需要放置在paddle/phi/kernels/linear_kernel.cc)
LinearKernel 的实现代码如下:
#include ...
#include "paddle/phi/kernels/elementwise_add_kernel.h"
#include "paddle/phi/kernels/elementwise_multiply_kernel.h"
template <typename T, typename Context>
void LinearKernel(const Context& dev_ctx,
const DenseTensor& x,
const DenseTensor& w,
const DenseTensor& b,
DenseTensor* out) {
dev_ctx.template Alloc<T>(out); // 为 out 分配内存
MultiplyKernel<T>(dev_ctx, x, w, out); // 复用 MultiplyKernel
AddKernel<T>(dev_ctx, out, b, out); // 复用 AddKernel
}
复用 kernel 的流程包括:
在源文件中 include 要复用 kernel 的头文件
直接调用相应的 kernel 函数进行复用
注意:设备无关 kernel 实现时计算逻辑部分只能复用现有 kernel 或设备无关的 functor,不能使用设备相关的语法或者函数接口(如 cuda、cudnn 等)进行计算处理
(2)实现设备相关 Kernel 函数
此处 trace 算子的 kernel 属于与设备相关的情况,CPU 和 GPU kernel 需要分别实现。
CPU kernel 实现位于:paddle/phi/kernels/cpu/trace_kernel.cc
GPU kernel 实现位于:paddle/phi/kernels/gpu/trace_kernel.cu
下面为 TraceKernel 的 CPU 实现为例介绍:
template <typename T, typename Context>
void TraceKernel(const Context& dev_ctx,
const DenseTensor& x,
int offset,
int axis1,
int axis2,
DenseTensor* out) {
auto* out_data = dev_ctx.template Alloc<T>(out);
const DenseTensor diag =
funcs::Diagonal<T, Context>(dev_ctx, &x, offset, axis1, axis2);
if (diag.numel() > 0) {
auto x = phi::EigenMatrix<T>::Reshape(diag, diag.dims().size() - 1);
auto output = phi::EigenVector<T>::Flatten(*out);
auto reduce_dim = Eigen::array<int, 1>({1});
output.device(*dev_ctx.eigen_device()) = x.sum(reduce_dim);
out->Resize(out->dims());
} else {
std::fill(out_data, out_data + out->numel(), static_cast<T>(0));
}
}
此处 TraceKernel 的实现并未复用其他 kernel,但如果有需要也是可以复用的,kernel 复用时,同样是直接 include 相应 kernel 头文件,在函数中调用即可,例如 triangular_solve_kernel 复用 empty 和 expand kernel。
首先在 triangular_solve_kernel.cc 头部 include 相应头文件:
#include "paddle/phi/kernels/empty_kernel.h"
#include "paddle/phi/kernels/expand_kernel.h"
然后在 kernel 实现中即可直接调用以上两个头文件中的 kernel,代码片段如下:
// Tensor broadcast to 'out' and temp 'x_bst'
IntArray x_bst_dims(x_bst_dims_vec);
DenseTensor x_bst = phi::Empty<T, Context>(dev_ctx, x_bst_dims);
const T* x_bst_data = x_bst.data<T>();
ExpandKernel<T, Context>(dev_ctx, x, x_bst_dims, &x_bst);
说明:对于 kernel 内部临时使用的
DenseTensor目前推荐使用Empty、EmptyLike、Full和FullLike接口进行创建。
(3)实现反向 Kernel 函数
反向 kernel 的实现与前向是类似的,此处不再赘述,可以直接参考对应链接中的代码实现。
(4)公共函数管理
如果有一些函数会被多个 kernel 调用,可以创建非 kernel 的文件管理代码,规则如下:
仅有当前 kernel 使用的辅助函数(具体到设备,比如 trace 的 cpu kernel),一律和 kernel 实现放到同一个设备文件夹中
如果辅助函数相关代码较少,就直接和 kernel 实现放到同一个
.cc/cu中如果辅助函数相关代码较多,就在 kernel 所在的设备目录创建
.h管理代码
有同设备多个 kernel 使用的辅助函数,在 kernel 所在的设备目录创建
.h放置代码有跨设备多个 kernel 使用的辅助函数,在
kernels/funcs目录下创建.h/cc/cu管理代码如果当前依赖的辅助函数可以直接归类到
kernels/funcs目录下已有的文件中,则直接放过去,不用创建新的文件
4.2.3 注册 Kernel 函数¶
在对应的 kernel 实现代码中添加注册 kernel 函数,直接使用注册宏注册即可,示例如下:
PD_REGISTER_KERNEL(trace,
CPU,
ALL_LAYOUT,
phi::TraceKernel,
float,
double,
int,
int64_t,
phi::dtype::float16,
phi::dtype::complex<float>,
phi::dtype::complex<double>) {}
字段说明:
trace: kernel 名称,和算子的名称一致CPU: backend 名称, 一般主要就是 CPU 和 GPUALL_LAYOUT: kernel 支持的 Tensor 布局,一般为 ALL_LAYOUT,及支持所有布局类型phi::TraceKernel: kernel 的函数名称,记得带上 namespace phi剩余的均为 kernel 支持的数据类型
注意:
如果忘记添加注册相关的头文件,会给出一个 error: expected constructor, destructor, or type conversion before ‘(’ token 的错误,如果遇到,请检查 include 的头文件;
phi 下的注册宏后边是带函数体{ },不是直接加分号,此处与旧的注册宏方式有小区别;
注册 kernel 的宏声明需要在 global namespace。
4.3 编译测试¶
实现完算子 kernel 之后,建议先编译测试一下,编译成功之后,再继续后面的步骤。
详细的编译环境准备和执行流程可参考 从源码编译,下面简单介绍几个主要步骤。 在 Paddle 代码目录下创建并切换到 build 目录:
mkdir build && cd build
执行cmake命令,具体选项可参考 从源码编译 中的介绍,下面的命令为编译 Python3.7,GPU 版本,带测试,Release 版本的 Paddle。
cmake .. -DPY_VERSION=3.7 -DWITH_GPU=ON -DWITH_TESTING=ON -DCMAKE_BUILD_TYPE=Release
在build目录下,运行下面命令可以进行编译整个 paddle:
make -j$(nproc)
**注意:**新增算子后请重新执行
cmake命令,然后再执行make命令编译 paddle。
五、封装 Python API¶
飞桨框架会对新增的算子 kernel 自动绑定 Python,并链接到生成的 lib 库中,然后开发者需要在 Python 端定义相应的 API,在 API 内调用新增算子,并添加相应的中英文文档描述即可。
paddle.trace 的 Python API 实现位于 python/paddle/tensor/math.py 中,具体实现如下:
def trace(x, offset=0, axis1=0, axis2=1, name=None):
"""
**trace**
This OP computes the sum along diagonals of the input tensor x.
If ``x`` is 2D, returns the sum of diagonal.
If ``x`` has larger dimensions, then returns an tensor of diagonals sum, diagonals be taken from
the 2D planes specified by axis1 and axis2. By default, the 2D planes formed by the first and second axes
of the input tensor x.
The argument ``offset`` determines where diagonals are taken from input tensor x:
- If offset = 0, it is the main diagonal.
- If offset > 0, it is above the main diagonal.
- If offset < 0, it is below the main diagonal.
- Note that if offset is out of input's shape indicated by axis1 and axis2, 0 will be returned.
Args:
x(Tensor): The input tensor x. Must be at least 2-dimensional. The input data type should be float32, float64, int32, int64.
offset(int, optional): Which diagonals in input tensor x will be taken. Default: 0 (main diagonals).
axis1(int, optional): The first axis with respect to take diagonal. Default: 0.
axis2(int, optional): The second axis with respect to take diagonal. Default: 1.
name (str, optional): For details, please refer to :ref:`api_guide_Name`. Generally, no setting is required. Default: None.
Returns:
Tensor: the output data type is the same as input data type.
Examples:
.. code-block:: python
import paddle
case1 = paddle.randn([2, 3])
case2 = paddle.randn([3, 10, 10])
case3 = paddle.randn([3, 10, 5, 10])
data1 = paddle.trace(case1) # data1.shape = [1]
data2 = paddle.trace(case2, offset=1, axis1=1, axis2=2) # data2.shape = [3]
data3 = paddle.trace(case3, offset=-3, axis1=1, axis2=-1) # data2.shape = [3, 5]
"""
def __check_input(input, offset, dim1, dim2):
check_dtype(x.dtype, 'Input',
['int32', 'int64', 'float16', 'float32', 'float64'],
'trace')
input_shape = list(x.shape)
assert len(input_shape) >= 2, \
"The x must be at least 2-dimensional, " \
"But received Input x's dimensional: %s.\n" % \
len(input_shape)
axis1_ = axis1 if axis1 >= 0 else len(input_shape) + axis1
axis2_ = axis2 if axis2 >= 0 else len(input_shape) + axis2
assert ((0 <= axis1_) and (axis1_ < len(input_shape))), \
"The argument axis1 is out of range (expected to be in range of [%d, %d], but got %d).\n" \
% (-(len(input_shape)), len(input_shape) - 1, axis1)
assert ((0 <= axis2_) and (axis2_ < len(input_shape))), \
"The argument axis2 is out of range (expected to be in range of [%d, %d], but got %d).\n" \
% (-(len(input_shape)), len(input_shape) - 1, axis2)
assert axis1_ != axis2_, \
"axis1 and axis2 cannot be the same axis." \
"But received axis1 = %d, axis2 = %d\n"%(axis1, axis2)
__check_input(input, offset, axis1, axis2)
if in_dygraph_mode():
return _C_ops.trace( x, offset, axis1, axis2 )
helper = LayerHelper('trace', **locals())
out = helper.create_variable_for_type_inference(dtype=x.dtype)
helper.append_op(
type='trace',
inputs={'Input': [x]},
attrs={'offset': offset,
'axis1': axis1,
'axis2': axis2},
outputs={'Out': [out]})
return out
Python API 实现要点(详见 开发 API Python 端)
对输入参数进行合法性检查,即
__check_input(input, offset, axis1, axis2)添加动态图分支调用,即
if in_dygraph_mode进入动态图调用分支添加静态图分支调用,即动态图分支后剩余的代码
六、添加单元测试¶
单测包括对比前向算子不同设备 (CPU、GPU) 的实现、对比反向算子不同设备 (CPU、GPU) 的实现、反向算子的梯度测试。下面介绍 trace 算子的单元测试。
单测文件存放路径和命名方式:在 python/paddle/fluid/tests/unittests 目录下,一般以 test_xxx_op.py 的形式命名(假设算子名为xxx),与 Python API 的单元测试文件命名为相同的前缀。
注意:单测中的测试用例需要尽可能地覆盖 kernel 中的所有分支。
6.1 C++ 算子单元测试¶
算子单元测试继承自 OpTest。各项具体的单元测试在TestTraceOp里完成。测试算子,需要:
在
setUp函数定义输入、输出,以及相关的属性参数,并生成随机的输入数据。在 Python 脚本中实现与前向算子相同的计算逻辑,得到输出值,与算子前向计算的输出进行对比。
反向计算已经自动集成进测试框架,直接调用相应接口即可。
import paddle
import unittest
import numpy as np
from op_test import OpTest
class TestTraceOp(OpTest):
# 配置 op 信息以及输入输出等参数
def setUp(self):
self.op_type = "trace"
self.python_api = paddle.trace
self.init_config()
self.outputs = {'Out': self.target}
# 测试前向输出结果
def test_check_output(self):
self.check_output(check_eager=True)
# 测试反向梯度输出
def test_check_grad(self):
self.check_grad(['Input'], 'Out', check_eager=True)
def init_config(self):
# 生成随机的输入数据
self.case = np.random.randn(20, 6).astype('float64')
self.inputs = {'Input': self.case}
self.attrs = {'offset': 0, 'axis1': 0, 'axis2': 1}
self.target = np.trace(self.inputs['Input'])
setUp 函数实现
self.op_type = "trace": 定义类型,与算子定义的名称相同。self.python_api = paddle.trace: 定义 python api,与 python 调用接口一致。self.inputs: 定义输入,类型为numpy.array,并初始化。self.outputs: 定义输出,并在 Python 脚本中完成与算子同样的计算逻辑,返回 Python 端的计算结果。
前向算子单测
test_check_output 中会对算子的前向计算结果进行测试,对比参考的结果为 setUp 中
self.outputs提供的数据。check_eager=True表示开启新动态图(eager 模式)单测,check_eager默认为False
反向算子单测
test_check_grad中调用check_grad使用数值法检测梯度正确性和稳定性。第一个参数
['Input']: 指定对输入变量Input做梯度检测。第二个参数
'Out': 指定前向网络最终的输出目标变量Out。第三个参数
check_eager:check_eager=True表示开启新动态图(eager 模式)单测,check_eager默认为False。
对于存在多个输入的反向算子测试,需要指定只计算部分输入梯度的 case
例如,test_elementwise_sub_op.py 中的
test_check_grad_ingore_x和test_check_grad_ingore_y分支用来测试只需要计算一个输入梯度的情况此处第三个参数 max_relative_error:指定检测梯度时能容忍的最大错误值。
def test_check_grad_ingore_x(self): self.check_grad( ['Y'], 'Out', max_relative_error=0.005, no_grad_set=set("X")) def test_check_grad_ingore_y(self): self.check_grad( ['X'], 'Out', max_relative_error=0.005, no_grad_set=set('Y'))
6.2 Python API 单元测试¶
Python API 也需要编写相关的单测进行测试,详见 开发 API Python 端。
其他有关单元测试添加的注意事项请参考 Op 开发手册 及 API 单测开发及验收规范。
6.3 运行单元测试¶
python/paddle/fluid/tests/unittests/ 目录下新增的 test_*.py 单元测试会被自动加入工程进行编译。
请注意,运行单元测试测时需要编译整个工程,并且编译时需要打开WITH_TESTING。
参考上述【4.3 编译测试】小节,编译成功后,在build目录下执行下面的命令来运行单元测试:
make test ARGS="-R test_trace_op -V"
或者执行:
ctest -R test_trace_op -V
七. 开发算子注意事项¶
7.1 报错检查¶
实现算子时检查数据的合法性需要使用 PADDLE_ENFORCE 以及 PADDLE_ENFORCE_EQ 等宏定义,基本格式如下:
PADDLE_ENFORCE(表达式, 错误提示信息)
PADDLE_ENFORCE_EQ(比较对象 A, 比较对象 B, 错误提示信息)
如果表达式为真,或者比较对象 A=B,则检查通过,否则会终止程序运行,向用户反馈相应的错误提示信息。 为了确保提示友好易懂,开发者需要注意其使用方法。
总体原则: 任何使用了 PADDLE_ENFORCE 与 PADDLE_ENFORCE_XX 检查的地方,必须有详略得当的备注解释!错误提示信息不能为空!
报错提示信息书写建议:
[required] 哪里错了?为什么错了?
例如:
ValueError: Mismatched label shape
[optional] 期望的输入是什么样的?实际的输入是怎样的?
例如:
Expected labels dimension=1. Received 4.
[optional] 能否给出修改意见?
例如:
Suggested Fix:If your classifier expects one-hot encoding label,check your n_classes argument to the estimatorand/or the shape of your label.Otherwise, check the shape of your label.
更详细的报错检查规范介绍请参考 《Paddle 报错信息文案书写规范》。
7.2 算子兼容性问题¶
对算子的修改需要考虑兼容性问题,要保证算子修改之后,之前的模型都能够正常加载及运行,即新版本的 Paddle 预测库能成功加载运行旧版本训练的模型。所以,需要保证算子当前的所有输入输出参数不能被修改(文档除外)或删除,可以新增参数,但是新增的 Tensor 类型变量需要设置为 optional,非 Tensor 变量需要设置默认值。更多详细内容请参考 OP 修改规范:Input/Output/Attribute 只能做兼容修改 。
7.3 显存优化¶
7.3.1 为可原位计算的算子注册 inplace¶
有些算子的计算逻辑中,输出可以复用输入的显存空间,也可称为原位计算。例如reshape中,输出out可以复用输入x的显存空间,因为该算子的计算逻辑不会改变x的实际数据,只是修改它的 shape,输出和输入复用同一块显存空间不影响结果。对于这类算子,可以注册inlace,从而让框架在运行时自动地进行显存优化。
注册方式为在算子的 YAML 配置中添加inplace配置项,格式如:(x -> out),详见YAML 配置规则。示例:
- op : reshape
args : (Tensor x, IntArray shape)
output : Tensor(out)
...
inplace : (x -> out)
7.3.2 减少反向算子中的无关变量¶
通常反向算子会依赖于前向算子的某些输入、输出 Tensor,以供反向算子计算使用。但有些情况下,反向算子不需要前向算子的所有输入和输出;有些情况下,反向算子只需要前向算子的部分输入和输出;有些情况下,反向算子只需要使用前向算子中输入和输出变量的 Shape 和 LoD 信息。若开发者在注册反向算子时,将不必要的前向算子输入和输出作为反向算子的输入,会导致这部分显存无法被框架现有的显存优化策略优化,从而导致模型显存占用过高。
所以在定义反向算子时需要注意以下几点:
如果反向不需要前向的某些输入或输出参数,则无需在 args 中设置。
如果有些反向算子需要依赖前向算子的输入或输出变量的的 Shape 或 LoD,但不依赖于变量中 Tensor 的内存 Buffer 数据,且不能根据其他变量推断出该 Shape 和 LoD,则可以通过
no_need_buffer对该变量进行配置,详见YAML 配置规则。示例:
- backward_op : trace_grad
forward : trace (Tensor x, int offset, int axis1, int axis2) -> Tensor(out)
args : (Tensor x, Tensor out_grad, int offset, int axis1, int axis2)
output : Tensor(x_grad)
...
no_need_buffer : x
7.4 性能优化¶
7.4.1 第三方库的选择¶
在写算子过程中优先使用高性能(如 cudnn、mkldnn、mklml、eigen 等)中提供的操作,但是一定要做 benchmark,有些库中的操作在深度学习任务中可能会比较慢。因为高性能库(如 eigen 等)中提供的操作为了更为通用,在性能方面可能并不是很好,通常深度学习模型中数据量较小,所以有些情况下可能高性能库中提供的某些操作速度较慢。比如 Elementwise 系列的所有算子(前向和反向),Elementwise 操作在模型中调用的次数比较多,尤其是 Elementwise_add,在很多操作之后都需要添加偏置项。在之前的实现中 Elementwise_op 直接调用 Eigen 库,由于 Elementwise 操作在很多情况下需要对数据做 Broadcast,而实验发现 Eigen 库做 Broadcast 的速度比较慢,慢的原因在这个 PR (#6229) 中有描述。
7.4.2 算子性能优化¶
算子的计算速度与输入的数据量有关,对于某些算子可以根据输入数据的 Shape 和算子的属性参数来选择不同的计算方式。比如 concat_op,当 axis>=1 时,在对多个 tensor 做拼接过程中需要对每个 tensor 做很多次拷贝,如果是在 GPU 上,需要调用 cudaMemCopy。相对 CPU 而言,GPU 属于外部设备,所以每次调用 GPU 的操作都会有一定的额外开销,并且当需要拷贝的次数较多时,这种开销就更为凸现。目前 concat_op 的实现会根据输入数据的 Shape 以及 axis 值来选择不同的调用方式,如果输入的 tensor 较多,且 axis 不等于 0,则将多次拷贝操作转换成一个 CUDA Kernel 来完成;如果输入 tensor 较少,且 axis 等于 0,使用直接进行拷贝。相关实验过程在该 PR (#8669) 中有介绍。
由于 CUDA Kernel 的调用有一定的额外开销,所以如果算子中出现多次调用 CUDA Kernel,可能会影响算子的执行速度。比如之前的 sequence_expand_op 中包含很多 CUDA Kernel,通常这些 CUDA Kernel 处理的数据量较小,所以频繁调用这样的 Kernel 会影响算子的计算速度,这种情况下最好将这些小的 CUDA Kernel 合并成一个。在优化 sequence_expand_op 过程中就是采用这种思路,相关 PR (#9289),优化后的 sequence_expand_op 比之前的实现平均快出约 1 倍左右,相关实验细节在该 PR (#9289) 中有介绍。
减少 CPU 与 GPU 之间的拷贝和同步操作的次数。比如 fetch 操作,在每个迭代之后都会对模型参数进行更新并得到一个 loss,并且数据从 GPU 端到没有页锁定的 CPU 端的拷贝是同步的,所以频繁的 fetch 多个参数会导致模型训练速度变慢。
更多算子性能优化方法,请参考 算子性能优化 方法介绍。
7.5 稀疏梯度参数更新方法¶
目前稀疏梯度在做更新的时候会先对梯度做 merge,即对相同参数的梯度做累加,然后做参数以及附加参数(如 velocity)的更新。
7.6 混合设备调用¶
由于 GPU 是异步执行的,当 CPU 调用返回之后,GPU 端可能还没有真正的执行,所以如果在算子中创建了 GPU 运行时需要用到的临时变量,当 GPU 开始运行的时候,该临时变量可能在 CPU 端已经被释放,这样可能会导致 GPU 计算出错。
关于 GPU 中的一些同步和异步操作:
The following device operations are asynchronous with respect to the host:
Kernel launches;
Memory copies within a single device's memory;
Memory copies from host to device of a memory block of 64 KB or less;
Memory copies performed by functions that are suffixed with Async;
Memory set function calls.
关于 cudaMemCpy 和 cudaMemCpyAsync 注意事项:
如果数据传输是从 GPU 端到非页锁定的 CPU 端,数据传输将是同步,即使调用的是异步拷贝操作。
如果数据传输是从 CPU 端到 CPU 端,数据传输将是同步的,即使调用的是异步拷贝操作。
更多内容可参考:Asynchronous Concurrent Execution,API synchronization behavior
7.7 算子数值稳定性问题¶
有些算子存在数值稳定性问题,出现数值稳定性的主要原因程序在多次运行时,对浮点型数据施加操作的顺序可能不同,进而导致最终计算结果不同。而 GPU 是通过多线程并行计算的方式来加速计算的,所以很容易出现对浮点数施加操作的顺序不固定现象。
目前发现 cudnn 中的卷积操作、cudnn 中的 MaxPooling、CUDA 中 CudaAtomicXX、ParallelExecutor 的 Reduce 模式下参数梯度的聚合等操作运行结果是非确定的。
为此 Paddle 中添加了一些 FLAGS,比如使用 FLAGS_cudnn_deterministic 来强制 cudnn 使用确定性算法、FLAGS_cpu_deterministic 强制 CPU 端的计算使用确定性方法。
7.8 算子的数学公式¶
如果算子有数学公式,一定要在代码中将数学公式写明,并在 Python API 的 Doc 中显示,因为用户在对比不同框架的计算结果时可能需要了解 Paddle 对算子是怎么实现的。
7.9 LoD 在算子内部的传导规范¶
LoD 是 Paddle 框架用来表示变长序列数据的属性,除了仅支持输入是 padding data 的算子外,所有算子的实现都要考虑 LoD 的传导问题。
根据算子的计算过程中是否用到 LoD,我们可以将涉及到 LoD 传导问题的算子分为两类: LoD-Transparent 与 LoD-Based。
| 类型 | 特点 | 示例 |
|---|---|---|
| LoD-Transparent | 计算过程不依赖 LoD,输入是否有 LoD 不会影响计算的结果,通常是 position-wise 的计算 | conv2d_op、batch_norm_op、dropout_op 等 |
| LoD-Based | 计算以序列为单位, 计算过程依赖 LoD | lstm_op、gru_op、sequence_ops 等 |
这两类算子的 LoD 传导需要考虑前向和反向两个过程。
(1)前向传导
在前向传导过程,与输入的 LoD 相比较,算子输出的 LoD 可能出现不变、改变和消失这三种情况:
不变:适用于所有的 LoD-Transparent 算子与部分的 LoD-Based 算子。可以在
InferMeta中调用ShareLoD()直接将输入 Var 的 LoD 共享给输出 Var, 可参考 lstm_op; 如果有多个输入且都可能存在 LoD 的情况,通常默认共享第一个输入, 例如 elementwise_ops forward;改变:适用于部分 LoD-Based 算子。在实现 OpKernel 时需考虑输出 LoD 的正确计算,真实的 LoD 在前向计算结束后才能确定,此时仍需要在
InferMeta中调用ShareLoD(),以确保 CompileTime 时对 LoD Level 做了正确的传导,可参考 sequence_expand_op;消失:适用于输出不再是序列数据的 LoD-Based 算子。此时不用再考虑前向的 LoD 传导问题,可参考 sequence_pool_op;
其它重要的注意事项:
实现 LoD-Based 算子时,需要处理好 LoD 传导的边界情况,例如对长度为零的输入的支持,并完善相应的单测,单测 case 覆盖空序列出现在 batch 开头、中间和末尾等位置的情况,可参考 test_lstm_op.py
对 LoD Level 有明确要求的算子,推荐的做法是在
InferMeta中即完成 LoD Level 的检查,例如 sequence_pad_op。
(2)反向传导
通常来讲,算子的某个输入 Var 所对应的梯度 GradVar 的 LoD 应该与 Var 自身相同,所以应直接将 Var 的 LoD 共享给 GradVar,可以参考 elementwise ops 的 backward。
八、更多信息¶
8.1 Paddle 基于 Yaml 配置自动生成算子代码的逻辑解读¶
Paddle 支持动态图和静态图两种模式,在 YAML 配置文件中完成算子基本属性的定义后,需要进行解析并分别生成动态图和静态图所对应的算子代码逻辑,从而将算子接入框架的执行体系。基于 YAML 配置的算子代码自动生成示意图,如下所示。
说明:当开发者添加一个新的 C++ 算子时,只需要完成下图中 Kernel、算子定义 Yaml 配置文件和 Python API 三个绿色框中的代码开发,其余橙色部分都会通过自动代码生成来完成,从而将新增算子接入飞桨框架中。
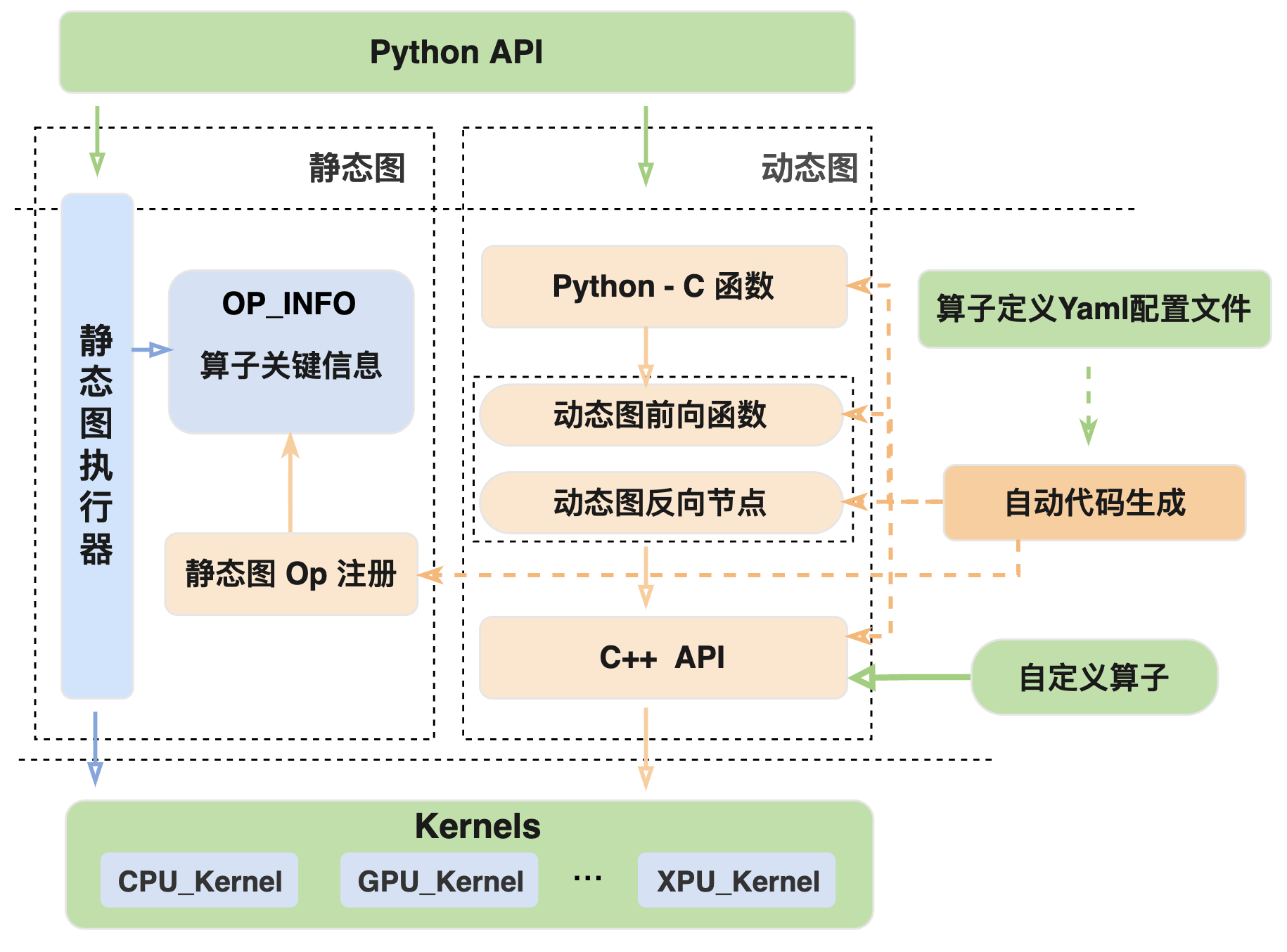
如前文所述,算子开发时通过 YAML 配置文件对算子进行描述及定义,包括前向 paddle/phi/api/yaml/ops.yaml 和反向 paddle/phi/api/yaml/backward.yaml。动态图和静态图两种模式的执行流程不同,具体如下所示:
动态图中自动生成的代码包括从 Python API 到计算 Kernel 间的各层调用接口实现,从底层往上分别为:
C++ API:一套与 Python API 参数对齐的 C++ 接口(只做逻辑计算,不支持自动微分),内部封装了底层 kernel 的选择和调用等逻辑,供上层灵活使用。
注:前向算子生成 C++ API 头文件和实现代码分别为
paddle/phi/api/include/api.h和paddle/phi/api/lib/api.cc,反向算子生成的头文件和实现代码分别为paddle/phi/api/backward/backward_api.h,paddle/phi/api/lib/backward_api.cc。
动态图前向函数与反向节点(Autograd API):在 C++ API 的基础上进行了封装,组成一个提供自动微分功能的 C++函数接口。
注:生成的相关代码在
paddle/fluid/eager/api/generated/eager_generated目录下。
Python-C 函数:将支持自动微分功能的 C++ 的函数接口(Autograd API)暴露到 Python 层供 Python API 调用。
注:生成的 Python-C 接口代码在
paddle/fluid/pybind/eager_op_function.cc中。
静态图的执行流程与动态图不同,所以生成的代码也与动态图有较大差异。
静态图由于是先组网后计算,Python API 主要负责组网,算子的调度和 kernel 计算由静态图执行器来完成,因此自动生成的代码是将配置文件中的算子信息注册到框架内供执行器调度,主要包括 OpMaker(静态图中定义算子的输入、输出以及属性等信息)和REGISTER_OPERATOR(将算子名称以及 OpMaker 等信息进行注册)等静态图算子注册组件,具体的代码逻辑可参考 paddle/fluid/operators/generated_op.cc。
注意:由于代码自动生成在编译时进行,所以查看上述生成代码需要先完成 框架的编译。