使用样例¶
一、 使用 @to_static 进行动静转换¶
动静转换(@to_static)通过解析 Python 代码(抽象语法树,下简称:AST) 实现一行代码即可将动态图转为静态图的功能,只需在待转化的函数前添加一个装饰器 @paddle.jit.to_static 。
如下是使用 @to_static 进行动静转换的两种方式:
方式一:使用 @to_static 装饰器装饰
SimpleNet(继承了nn.Layer) 的forward函数:import paddle from paddle.jit import to_static class SimpleNet(paddle.nn.Layer): def __init__(self): super(SimpleNet, self).__init__() self.linear = paddle.nn.Linear(10, 3) @to_static # 动静转换 def forward(self, x, y): out = self.linear(x) out = out + y return out net = SimpleNet() net.eval() x = paddle.rand([2, 10]) y = paddle.rand([2, 3]) out = net(x, y) paddle.jit.save(net, './net')方式二:调用
paddle.jit.to_static()函数,仅做预测模型导出时推荐此种用法。import paddle from paddle.jit import to_static class SimpleNet(paddle.nn.Layer): def __init__(self): super(SimpleNet, self).__init__() self.linear = paddle.nn.Linear(10, 3) def forward(self, x, y): out = self.linear(x) out = out + y return out net = SimpleNet() net.eval() net = paddle.jit.to_static(net) # 动静转换 x = paddle.rand([2, 10]) y = paddle.rand([2, 3]) out = net(x, y) paddle.jit.save(net, './net')
方式一和方式二的主要区别是,使用 @to_static 除了支持预测模型导出外,在模型训练时,还会转为静态图子图训练,而方式二仅支持预测模型导出。@to_static 的基本执行流程如下图:
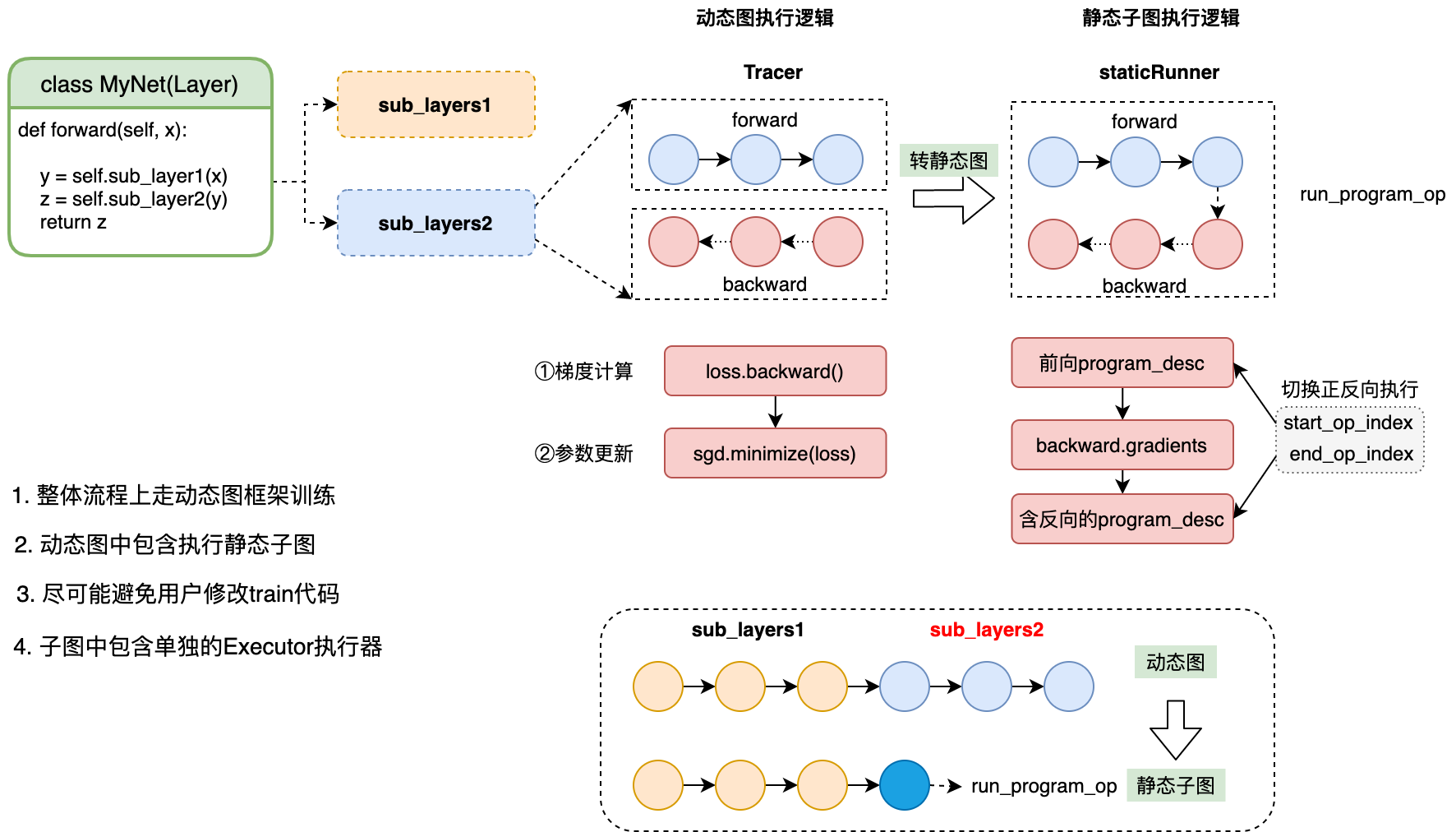
二、动转静模型导出¶
动转静模块是架在动态图与静态图的一个桥梁,旨在打破动态图模型训练与静态部署的鸿沟,消除部署时对模型代码的依赖,打通与预测端的交互逻辑。下图展示了动态图模型训练——>动转静模型导出——>静态预测部署的流程。
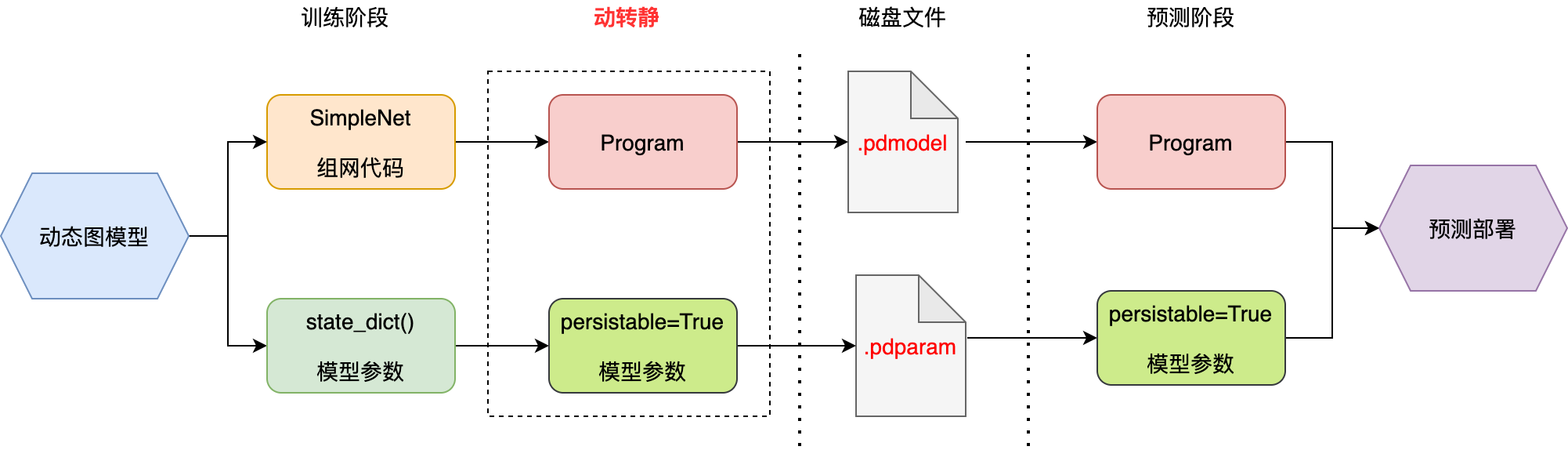
在处理逻辑上,动转静主要包含两个主要模块:
代码层面:将模型中所有的
layers接口在静态图模式下执行以转为Op,从而生成完整的静态ProgramTensor层面:将所有的
Parameters和Buffers转为可导出的Variable参数(persistable=True)
2.1 通过 forward 导出预测模型¶
通过 forward 导出预测模型导出一般包括三个步骤:
切换
eval()模式:类似Dropout、LayerNorm等接口在train()和eval()的行为存在较大的差异,在模型导出前,请务必确认模型已切换到正确的模式,否则导出的模型在预测阶段可能出现输出结果不符合预期的情况。构造
InputSpec信息:InputSpec 用于表示输入的shape、dtype、name信息,且支持用None表示动态shape(如输入的 batch_size 维度),是辅助动静转换的必要描述信息。调用
save接口:调用paddle.jit.save接口,若传入的参数是类实例,则默认对forward函数进行@to_static装饰,并导出其对应的模型文件和参数文件。
如下是一个简单的示例:
import paddle
from paddle.jit import to_static
from paddle.static import InputSpec
class SimpleNet(paddle.nn.Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
def forward(self, x, y):
out = self.linear(x)
out = out + y
return out
def another_func(self, x):
out = self.linear(x)
out = out * 2
return out
net = SimpleNet()
# train(net) 模型训练 (略)
# step 1: 切换到 eval() 模式
net.eval()
# step 2: 定义 InputSpec 信息
x_spec = InputSpec(shape=[None, 3], dtype='float32', name='x')
y_spec = InputSpec(shape=[3], dtype='float32', name='y')
# step 3: 调用 jit.save 接口
net = paddle.jit.save(net, path='simple_net', input_spec=[x_spec, y_spec]) # 动静转换
执行上述代码样例后,在当前目录下会生成三个文件,即代表成功导出预测模型:
simple_net.pdiparams // 存放模型中所有的权重数据
simple_net.pdimodel // 存放模型的网络结构
simple_net.pdiparams.info // 存放额外的其他信息
2.2 使用 InputSpec 指定模型输入 Tensor 信息¶
动静转换在生成静态图 Program 时,依赖输入 Tensor 的 shape、dtype 和 name 信息。因此,Paddle 提供了 InputSpec 接口,用于指定输入 Tensor 的描述信息,并支持动态 shape 特性。
2.2.1 构造 InputSpec¶
方式一:直接构造
InputSpec 接口在 paddle.static 目录下, 只有 shape 是必须参数, dtype 和 name 可以缺省,默认取值分别为 float32 和 None 。使用样例如下:
from paddle.static import InputSpec
x = InputSpec([None, 784], 'float32', 'x')
label = InputSpec([None, 1], 'int64', 'label')
print(x) # InputSpec(shape=(-1, 784), dtype=VarType.FP32, name=x)
print(label) # InputSpec(shape=(-1, 1), dtype=VarType.INT64, name=label)
方式二:由 Tensor 构造
可以借助 InputSpec.from_tensor 方法,从一个 Tensor 直接创建 InputSpec 对象,其拥有与源 Tensor 相同的 shape 和 dtype 。 使用样例如下:
import numpy as np
import paddle
from paddle.static import InputSpec
x = paddle.to_tensor(np.ones([2, 2], np.float32))
x_spec = InputSpec.from_tensor(x, name='x')
print(x_spec) # InputSpec(shape=(2, 2), dtype=VarType.FP32, name=x)
注:若未在
from_tensor中指定新的name,则默认使用与源 Tensor 相同的name。
方式三:由 numpy.ndarray
也可以借助 InputSpec.from_numpy 方法,从一个 Numpy.ndarray 直接创建 InputSpec 对象,其拥有与源 ndarray 相同的 shape 和 dtype 。使用样例如下:
import numpy as np
from paddle.static import InputSpec
x = np.ones([2, 2], np.float32)
x_spec = InputSpec.from_numpy(x, name='x')
print(x_spec) # InputSpec(shape=(2, 2), dtype=VarType.FP32, name=x)
注:若未在
from_numpy中指定新的name,则默认使用None。
2.2.2 基本用法¶
方式一: 在 @to_static 装饰器中调用
如下是一个简单的使用样例:
import paddle
from paddle.nn import Layer
from paddle.jit import to_static
from paddle.static import InputSpec
class SimpleNet(Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
@to_static(input_spec=[InputSpec(shape=[None, 10], name='x'), InputSpec(shape=[3], name='y')])
def forward(self, x, y):
out = self.linear(x)
out = out + y
return out
net = SimpleNet()
# save static model for inference directly
paddle.jit.save(net, './simple_net')
在上述的样例中, @to_static 装饰器中的 input_spec 为一个 InputSpec 对象组成的列表,用于依次指定参数 x 和 y 对应的 Tensor 签名信息。在实例化 SimpleNet 后,可以直接调用 paddle.jit.save 保存静态图模型,不需要执行任何其他的代码。
注:
input_spec 参数中不仅支持 InputSpec 对象,也支持 int 、 float 等常见 Python 原生类型。
若指定 input_spec 参数,则需为被装饰函数的所有必选参数都添加对应的 InputSpec 对象,如上述样例中,不支持仅指定 x 的签名信息。
若被装饰函数中包括非 Tensor 参数,推荐函数的非 Tensor 参数设置默认值,如
forward(self, x, use_bn=False)
方式二:在 to_static 函数中调用
若期望在动态图下训练模型,在训练完成后保存预测模型,并指定预测时需要的签名信息,则可以选择在保存模型时,直接调用 to_static 函数。使用样例如下:
class SimpleNet(Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
def forward(self, x, y):
out = self.linear(x)
out = out + y
return out
net = SimpleNet()
# train process (Pseudo code)
for epoch_id in range(10):
train_step(net, train_reader)
net = to_static(net, input_spec=[InputSpec(shape=[None, 10], name='x'), InputSpec(shape=[3], name='y')])
# save static model for inference directly
paddle.jit.save(net, './simple_net')
如上述样例代码中,在完成训练后,可以借助 to_static(net, input_spec=...) 形式对模型实例进行处理。Paddle 会根据 input_spec 信息对 forward 函数进行递归的动转静,得到完整的静态图,且包括当前训练好的参数数据。
方式三:通过 list 和 dict 推导
上述两个样例中,被装饰的 forward 函数的参数均为 Tensor 。这种情况下,参数个数必须与 InputSpec 个数相同。但当被装饰的函数参数为 list 或 dict 类型时,input_spec 需要与函数参数保持相同的嵌套结构。
当函数的参数为 list 类型时,input_spec 列表中对应元素的位置,也必须是包含相同元素的 InputSpec 列表。使用样例如下:
class SimpleNet(Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
@to_static(input_spec=[[InputSpec(shape=[None, 10], name='x'), InputSpec(shape=[3], name='y')]])
def forward(self, inputs):
x, y = inputs[0], inputs[1]
out = self.linear(x)
out = out + y
return out
其中 input_spec 参数是长度为 1 的 list ,对应 forward 函数的 inputs 参数。 input_spec[0] 包含了两个 InputSpec 对象,对应于参数 inputs 的两个 Tensor 签名信息。
当函数的参数为dict时, input_spec 列表中对应元素的位置,也必须是包含相同键(key)的 InputSpec 列表。使用样例如下:
class SimpleNet(Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
@to_static(input_spec=[InputSpec(shape=[None, 10], name='x'), {'x': InputSpec(shape=[3], name='bias')}])
def forward(self, x, bias_info):
x_bias = bias_info['x']
out = self.linear(x)
out = out + x_bias
return out
其中 input_spec 参数是长度为 2 的 list ,对应 forward 函数的 x 和 bias_info 两个参数。 input_spec 的最后一个元素是包含键名为 x 的 InputSpec 对象的 dict ,对应参数 bias_info 的 Tensor 签名信息。
方式四:指定非Tensor参数类型
目前,to_static 装饰器中的 input_spec 参数仅接收 InputSpec 类型对象。若被装饰函数的参数列表除了 Tensor 类型,还包含其他如 Int、 String 等非 Tensor 类型时,推荐在函数中使用 kwargs 形式定义非 Tensor 参数,如下述样例中的 use_act 参数。
class SimpleNet(Layer):
def __init__(self, ):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
self.relu = paddle.nn.ReLU()
def forward(self, x, use_act=False):
out = self.linear(x)
if use_act:
out = self.relu(out)
return out
net = SimpleNet()
# 方式一:save inference model with use_act=False
net = to_static(input_spec=[InputSpec(shape=[None, 10], name='x')])
paddle.jit.save(net, path='./simple_net')
# 方式二:save inference model with use_act=True
net = to_static(input_spec=[InputSpec(shape=[None, 10], name='x'), True])
paddle.jit.save(net, path='./simple_net')
在上述样例中,假设 step 为奇数时,use_act 取值为 False ; step 为偶数时, use_act 取值为 True 。动转静支持非 Tensor 参数在训练时取不同的值,且保证了取值不同的训练过程都可以更新模型的网络参数,行为与动态图一致。
在借助 paddle.jit.save 保存预测模型时,动转静会根据 input_spec 和 kwargs 的默认值保存推理模型和网络参数。建议将 kwargs 参数默认值设置为预测时的取值。
更多关于动转静 to_static 搭配 paddle.jit.save/load 的使用方式,可以参考 【模型的存储与载入】。
三、动、静态图部署区别¶
当训练完一个模型后,下一阶段就是保存导出,实现模型和参数的分发,进行多端部署。如下两小节,将介绍动态图和静态图的概念和差异性,以帮助理解动转静如何起到桥梁作用的。
3.1 动态图预测部署¶
动态图下,模型指的是 Python 前端代码;参数指的是 model.state_dict() 中存放的权重数据。
net = SimpleNet()
# .... 训练过程(略)
layer_state_dict = net.state_dict()
paddle.save(layer_state_dict, "net.pdiparams") # 导出模型
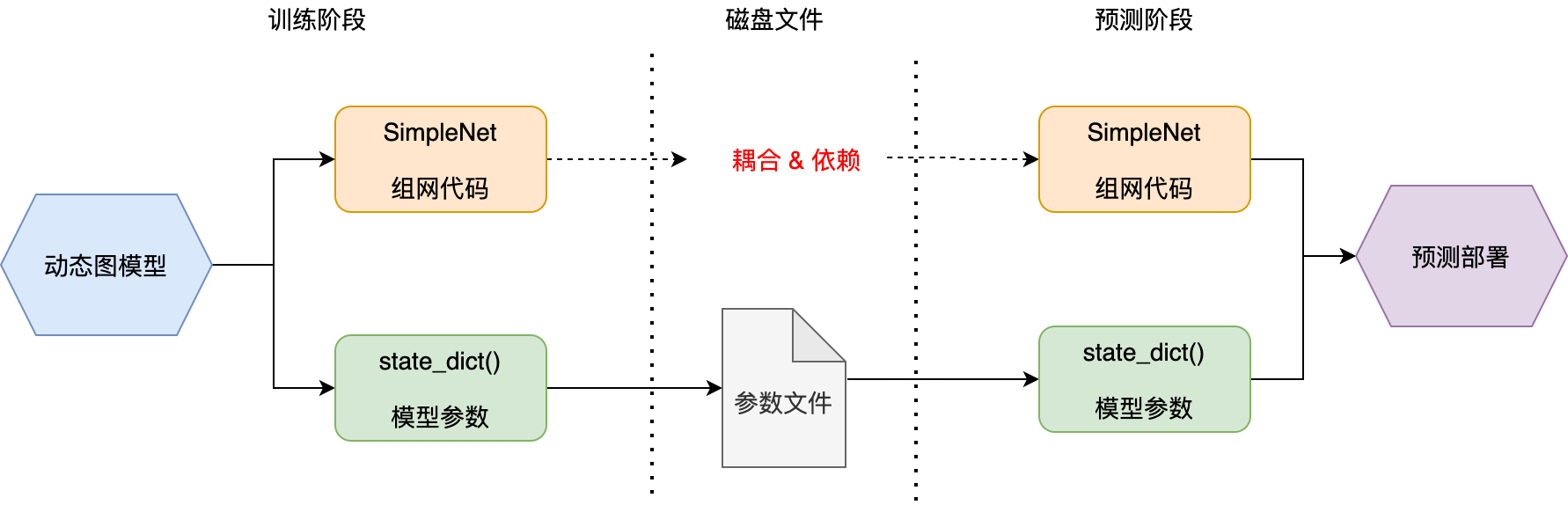
上图展示了动态图下模型训练——>参数导出——>预测部署的流程。如图中所示,动态图预测部署时,除了已经序列化的参数文件,还须提供最初的模型组网代码。
在动态图下,模型代码是 逐行被解释执行 的。如:
import paddle
zeros = paddle.zeros(shape=[1,2], dtype='float32')
print(zeros)
#Tensor(shape=[1, 2], dtype=float32, place=CPUPlace, stop_gradient=True,
# [[0., 0.]])
从框架层面上,上述的调用链是:
前端 zeros 接口 → core.ops.fill_constant (Pybind11) → 后端 Kernel → 前端 Tensor 输出
如下是一个简单的 Model 示例:
import paddle
class SimpleNet(paddle.nn.Layer):
def __init__(self):
super(SimpleNet, self).__init__()
self.linear = paddle.nn.Linear(10, 3)
def forward(self, x, y):
out = self.linear(x)
out = out + y
return out
net = SimpleNet()
动态图下,当实例化一个 SimpleNet() 对象时,隐式地执行了如下几个步骤:
创建一个
Linear对象,记录到self._sub_layer中(dict 类型)创建一个
ParamBase类型的weight,记录到self._parameters中(dict类型)创建一个
ParamBase类型的bias,记录到self._parameters中
一个复杂模型可能包含很多子类,框架层就是通过 self._sub_layer 和 self._parameters 两个核心数据结构关联起来的,这也是后续动转静原理上操作的两个核心属性。
sgd = paddle.optimizer.SGD(learning_rate=0.1, parameters=net.parameters())
^
|
所有待更新参数
3.2 静态图预测部署¶
静态图部署时,模型指的是 Program ;参数指的是所有的 Persistable=True 的 Variable 。二者都可以序列化导出为磁盘文件,与前端代码完全解耦。
main_program = paddle.static.default_main_program()
# ...... 训练过程(略)
prog_path='main_program.pdimodel'
paddle.save(main_program, prog_path) # 导出为 .pdimodel
para_path='main_program.pdiparams'
paddle.save(main_program.state_dict(), para_path) # 导出为 .pdiparams
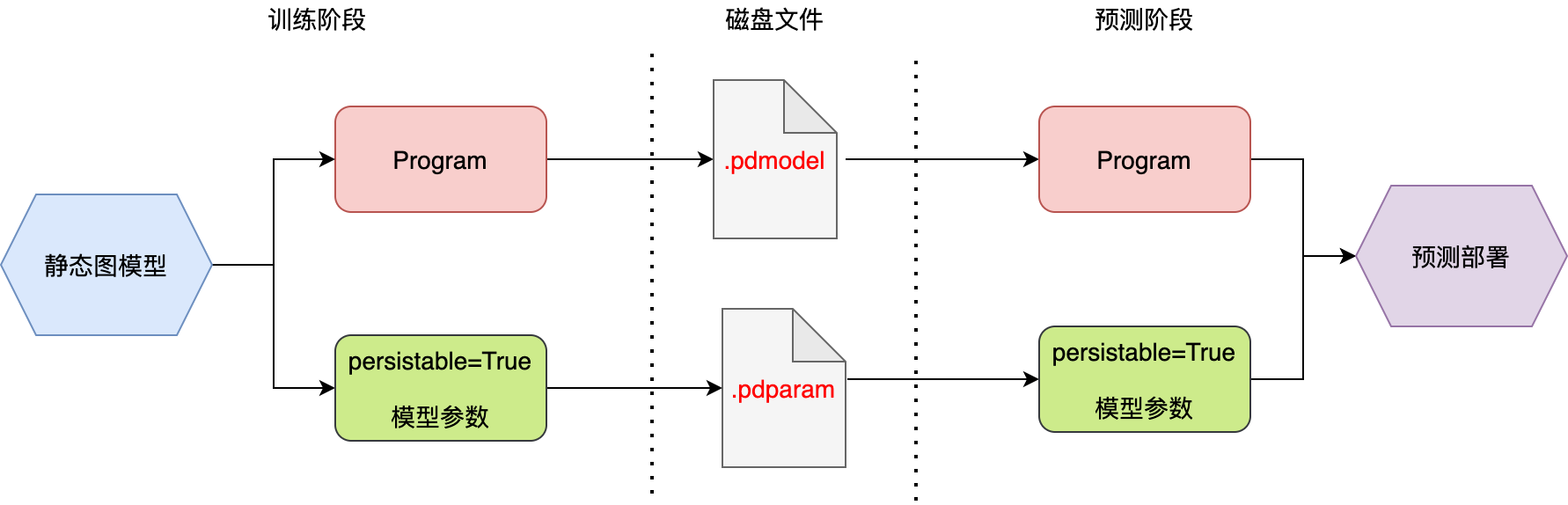
上图展示了静态图下模型训练——>模型导出——>预测部署的流程。如图所示,静态图模型导出时将Program和模型参数都导出为磁盘文件,Program 中包含了模型所有的计算描述( OpDesc ),不存在计算逻辑有遗漏的地方。
静态图编程,总体上包含两个部分:
编译期:组合各个
Layer接口,搭建网络结构,执行每个 Op 的InferShape逻辑,最终生成Program执行期:构建执行器,输入数据,依次执行每个
OpKernel,进行训练和评估
在静态图编译期,变量 Variable 只是一个符号化表示,并不像动态图 Tensor 那样持有实际数据。
import paddle
# 开启静态图模式
paddle.enable_static()
zeros = paddle.zeros(shape=[1,2], dtype='float32')
print(zeros)
# var fill_constant_1.tmp_0 : LOD_TENSOR.shape(1, 2).dtype(float32).stop_gradient(True)
从框架层面上,静态图的调用链:
layer 组网(前端) → InferShape 检查(编译期) → Executor(执行期) → 逐个执行 OP
如下是 SimpleNet 的静态图模式下的组网代码:
import paddle
# 开启静态图模式
paddle.enable_static()
# placeholder 信息
x = paddle.static.data(shape=[None, 10], dtype='float32', name='x')
y = paddle.static.data(shape=[None, 3], dtype='float32', name='y')
out = paddle.static.nn.fc(x, 3)
out = paddle.add(out, y)
# 打印查看 Program 信息
print(paddle.static.default_main_program())
# { // block 0
# var x : LOD_TENSOR.shape(-1, 10).dtype(float32).stop_gradient(True)
# var y : LOD_TENSOR.shape(-1, 3).dtype(float32).stop_gradient(True)
# persist trainable param fc_0.w_0 : LOD_TENSOR.shape(10, 3).dtype(float32).stop_gradient(False)
# var fc_0.tmp_0 : LOD_TENSOR.shape(-1, 3).dtype(float32).stop_gradient(False)
# persist trainable param fc_0.b_0 : LOD_TENSOR.shape(3,).dtype(float32).stop_gradient(False)
# var fc_0.tmp_1 : LOD_TENSOR.shape(-1, 3).dtype(float32).stop_gradient(False)
# var elementwise_add_0 : LOD_TENSOR.shape(-1, 3).dtype(float32).stop_gradient(False)
# {Out=['fc_0.tmp_0']} = mul(inputs={X=['x'], Y=['fc_0.w_0']}, force_fp32_output = False, op_device = , op_namescope = /, op_role = 0, op_role_var = [], scale_out = 1.0, scale_x = 1.0, scale_y = [1.0], use_mkldnn = False, x_num_col_dims = 1, y_num_col_dims = 1)
# {Out=['fc_0.tmp_1']} = elementwise_add(inputs={X=['fc_0.tmp_0'], Y=['fc_0.b_0']}, Scale_out = 1.0, Scale_x = 1.0, Scale_y = 1.0, axis = 1, mkldnn_data_type = float32, op_device = , op_namescope = /, op_role = 0, op_role_var = [], use_mkldnn = False, use_quantizer = False, x_data_format = , y_data_format = )
# {Out=['elementwise_add_0']} = elementwise_add(inputs={X=['fc_0.tmp_1'], Y=['y']}, Scale_out = 1.0, Scale_x = 1.0, Scale_y = 1.0, axis = -1, mkldnn_data_type = float32, op_device = , op_namescope = /, op_role = 0, op_role_var = [], use_mkldnn = False, use_quantizer = False, x_data_format = , y_data_format = )
}
静态图中的一些概念:
Program:与
Model对应,描述网络的整体结构,内含一个或多个BlockBlock
global_block:全局
Block,包含所有Parameters、全部Ops和Variablessub_block:控制流,包含控制流分支内的所有
Ops和必要的Variables
OpDesc:对应每个前端 API 的计算逻辑描述
Variable:对应所有的数据变量,如
Parameter,临时中间变量等,全局唯一name。
注:更多细节,请参考 【官方文档】模型的存储与载入。