非结构化稀疏是一种常见的模型压缩策略。本文中,我们将分享一套基于飞桨(PaddlePaddle) 的非结构化稀疏训练和推理的端到端系统,以及为保证训练精度与推理速度而做的优化策略。移动端实测 MobileNetV1,稀疏度 80%,精度损失小于 1%,FP32 和 INT8 模型推理加速 70% 和 60%;稀疏度 90%,精度损失 2.7%,FP32 和 INT8 加速 178% 和 132%。
近些年,深度学习正在经历从学术研究领域到工业落地方面的快速转变。一个完备的深度学习落地流程包括:模型设计、模型训练与调优、模型压缩、推理部署,最终成为在各种设备上快速、精准运行的人工智能系统。考虑到终端设备计算能力的限制,如何将研发产出的大模型转变为可以轻便部署、快速推理的小模型,就变得尤为重要了。模型压缩可以从软硬结合以及算法角度解决该问题,例如,量化方法将 32bit 的数值精度降低为 16bit、8bit 甚至更低,从而加速计算效率和减少内存带宽使用;剪枝方法则通过直接将不重要的参数剪裁掉,减小模型体积和运算次数,也就是模型稀疏化策略。
常见的稀疏方式可分为结构化稀疏和非结构化稀疏。前者在某个特定维度(特征通道、卷积核等等)上对卷积、矩阵乘法做剪枝操作,然后生成一个更小的模型结构,这样可以复用已有的卷积、矩阵乘计算,无需特殊实现推理算子;后者以每一个参数为单元稀疏化,然而并不会改变参数矩阵的形状,只是变成了含有大量零值的稀疏矩阵,所以更依赖于推理库、硬件对于稀疏后矩阵运算的加速能力。从效果上看,结构化稀疏在较低稀疏度时,还能使模型获得一定的加速能力,但是在高稀疏度时往往会引入较大的精度损失;非结构化稀疏更能在高稀疏度时,可以达到几倍的推理加速,同时精度损失不大。
我们基于飞桨的训练、压缩和推理部署框架,实现了一套非结构化稀疏的端到端系统,并且包含了诸多优化技巧,从而达到了快速训练和推理的目的。本篇文档会侧重方法和实战经验介绍,包含非结构化稀疏的训练技巧、部署推理实现及其优化技巧的整体思路等,其中推理部分主要是针对移动端(ARM CPU)的优化和测试。
绝大多数模型压缩策略都是应用在一个训练好的模型上,通过 Fine-tune,最终在精度损失很小的情况下,达到压缩目的。非结构化稀疏需要在剪裁后的模型上,进行全量数据集的稀疏化训练过程。在飞桨模型压缩工具 PaddleSlim 中,我们实现了非结构化稀疏算法*,不仅支持对权重数据类型为 FP32 模型的稀疏,还支持获得 INT8 的稀疏权重。以下三点是保证训练时间、精度以及最终压缩效果的关键。
*(非结构化稀疏算法:https://github.com/PaddlePaddle/PaddleSlim/tree/develop/demo/unstructured_prune)
稀疏化训练包含剪裁模型和 Fine-tune 训练等步骤,但是如何合理的剪裁模型,以保证训练精度呢?
这里以 50% 为目标稀疏度举例,讨论两种训练策略:
GMP(
Gradual Magnitude Pruning*
)就是一种分多步剪裁的训练策略,该方法有效提升了模型在大稀疏度下的收敛性能。区别于一步将模型剪裁到目标稀疏度,GMP 会将大的目标稀疏度拆分成很多个中间目标,通过逐步的训练和收敛完成训练。GMP 实际上是对随机梯度下降(SGD)的
隐性正则特性*
(Implicit regularization)或者显性的 L1、L2 正则项的适配。因为正则项会在训练过程中不断对不重要的权重做数值上的抑制,让这些权重的数值向 0 靠近,所以训练过程中,我们需要给正则留出调整稀疏化权重分布的时间,然后同时逐步调大稀疏度。
*(
Gradual Magnitude Pruning
https:
//arxiv.org/abs/1506.02626
)
*(隐性正特征:
https://arxiv.org/abs/1811.00659
)
总体来说,GMP 策略包含三个阶段:
稳定阶段、剪裁训练阶段和调优阶段
:
-
稳定阶段:
该阶段的目标稀疏度保持为 0,且占用训练时间很少(1-2 Epochs足够),用于正式剪裁前的模型稳定。由于我们已经导入了充分收敛的预训练权重,所以也就无需稳定阶段了。实验测试下来,也是发现它的有无对稀疏模型精度的影响很小,所以不着重分析了。
-
剪裁阶段:
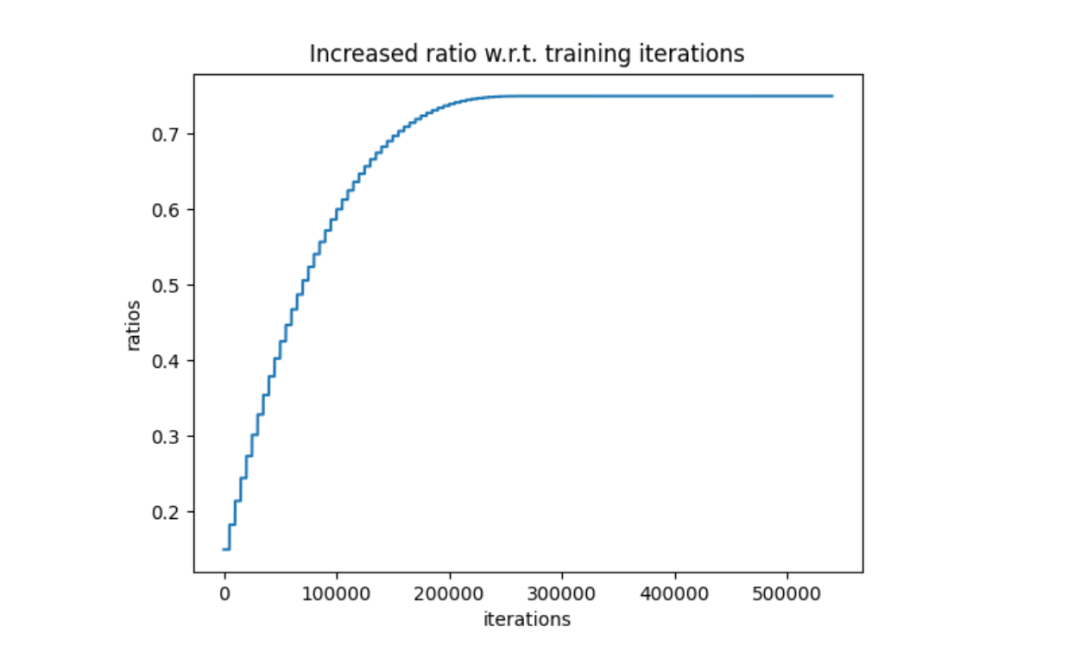
该阶段中,稀疏度从某一个初始值(Initial ratio)按三次函数过程增加到最终值(Target ratio),且增加的幅度逐渐减小,用于稳定稀疏训练。同时,学习率在该过程中维持不变或者轻微下降。

-
调优阶段:
该阶段中,稀疏度保持为最终值(Target ratio),学习率下降。
例如,对于一个需要 600000 步迭代的稀疏化训练过程,前 300000 步用于剪裁,稀疏度按照三次函数曲线减速上升;后 300000 步稀疏度维持不变。
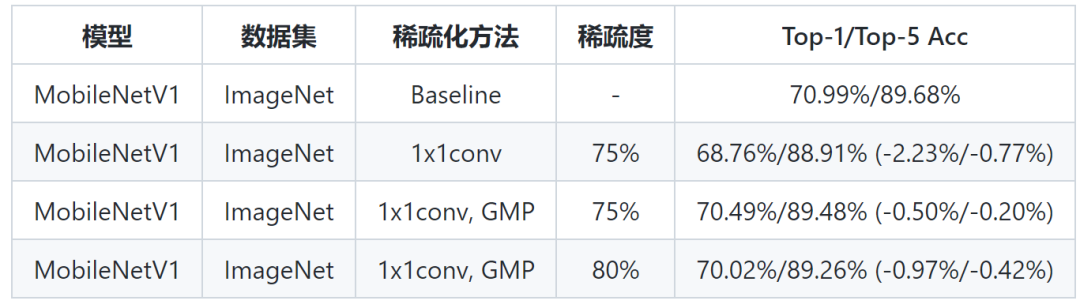
从上表可以看到,加入 GMP 后,模型精度有 1.73% 的提升。除了实验结果的验证,算法上我们为什么相信 GMP 优于一步剪裁策略(上表第二行结果)呢?这基于我们实现的权重重要性的评判指标:权重的绝对值越大,权重越重要。同时,这个重要性规律只在权重绝对值很大时,才有比较明显的体现,所以一步剪裁很可能直接移除了某些重要权重(但是数值不大),导致了最终的精度损失。GMP 解决这个问题的依据是训练过程中,正则项(例如上述 SGD 带来的
隐性正则特性
,L1、L2显性正则等)对某些权重大小带来的抑制作用,可以让网络不断地去调整稀疏化权重的分布。
稀疏策略上,另外一个重要的维度是如何将剪裁比例应用到不同层,比如,为使模型的整体稀疏度达到 50%,我们可以将所有权重一起排序,置零 50% (该方法称为 Global Sparsity),也可以对每一个权重矩阵分别排序然后置零 50%(该方法称为 Uniform Sparsity)。这两种做法虽然都能让模型稀疏度达到 50%,但是 Uniform Sparsity 额外保证了各个权重矩阵稀疏度均为 50%,Global Sparsity 可能会造成各个权重矩阵稀疏度不同的现象。具体矛盾如下:
-
Uniform Sparsity:
结合推理实现(推理实现优化章节介绍),因为每一个权重矩阵稀疏度都是 50%,都能够获得加速效果,对于模型的整体加速比较明显;但同时考虑到一些层比较重要(例如特征提取的浅层),强行规定稀疏度 50% 的话,可能对于精度恢复不是很友好。
-
Global Sparsity:
和 Uniform Sparsity 相对,Globel Sparsity 只保证了所有权重矩阵的平均稀疏度是 50%,所以潜在的会给重要的权重矩阵分配较低的稀疏度,所以精度恢复较好,但是由于某些层会存在 30% 甚至 10% 的稀疏度,使得推理速度变慢。
经过权衡和实验验证,我们推荐选取 Uniform Sparsity 的方案,以保证在精度损失允许范围内,获得显著加速性能。
3. 蒸馏对于 FP32 和 INT8 稀疏化模型的性能提升
蒸馏是一种非常有效的提升小模型精度并且加快收敛速度的方式,它具体是借助一个较大的预训练网络(Teacher network)来约束小网络(Student network)的训练收敛。根据任务的不同(视觉分类、视觉检测,语言学任务等等),我们可以设计不同的 Loss 完成蒸馏。更多介绍可以参照这篇论文综述:
Knowledge Distillation: A Survey*
。
*(Knowledge Distillation: A Survey:
https://arxiv.org/abs/2006.05525
)
经过工程实践,我们发现在稀疏化训练过程中,将稠密网络作为 Teacher,加入蒸馏 Loss,约束稀疏化网络,对于精度恢复和收敛速度提升可以起到明显的作用,具体而言,有如下两个特点:
-
收敛速度加快。
在分类任务上(MobileNetV1-ImageNet),收敛所需 Epoch 数减少。
-
精度提升,尤其是 INT8 模型。
同样在分类任务上(MobileNetV1-ImageNet),蒸馏 + PACT 量化训练甚至可以使稀疏 INT8 模型精度超过稠密 INT8 模型的精度。
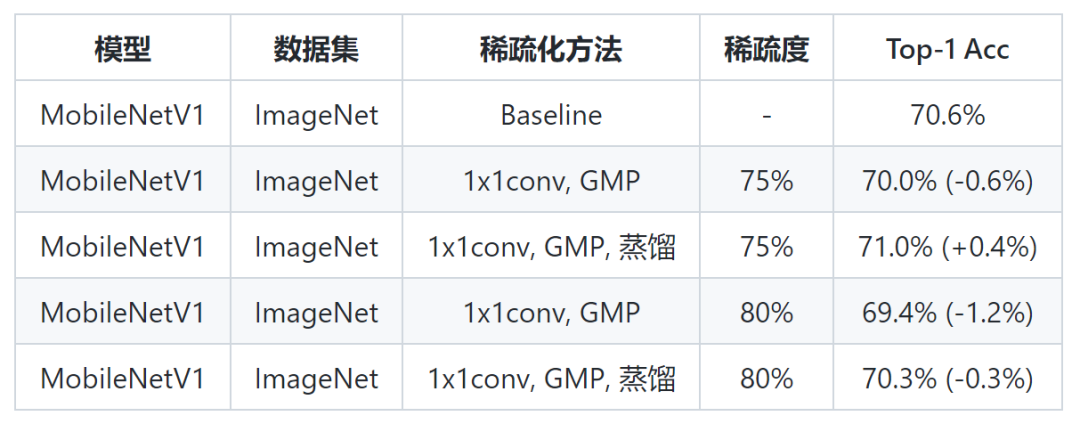
蒸馏带来的收益情况如下 (下表中均为 INT8 模型):
由于非结构化稀疏并没有改变权重矩阵的形状,只是置零了一部分权重的数值,所以我们需要自定义一些逻辑,达到推理时跳过这些 0 的目的。在飞桨轻量化推理引擎 Paddle Lite 中,实现了稀疏的 1x1 卷积算子,达到推理加速的目的。而 1x1 卷积等价于矩阵乘法,下面的描述均称作稀疏矩阵乘法。概括来看,稀疏矩阵乘法的推理实现包括:权重矩阵的 CSR 数据格式准备、特征矩阵分块、计算核函数实现三个步骤,以下一一介绍。
CSR(Compressed Sparse Row)/ CRS(Compressed Row Storage)代表一种稀疏矩阵的存储格式,其核心做法是只存储非零元素的数值和位置,以达到快速读取非零元素的目的。
由此带来如下特点:
-
由于需要存储和读取非零元素的index,造成了一定的时间开销,所以 CSR 格式在达到一定的稀疏度时,才能带来显著的加速效果。
-
在大多数情况下,CSR 格式的存储都会降低矩阵的存储体积(INT8 的数据的低稀疏度矩阵除外)。
与稠密矩阵乘法的分块优化相同,在稀疏矩阵乘法中采用相同的优化技巧。
在内存读取一个大矩阵时,为了方便预读取、读取与多线程操作,我们需要将大矩阵划分为若干符合内存大小的子块,从而加速推理速度。
例如,对于两个矩阵相乘(权重矩阵和特征矩阵形状分别为 MxK,KxN),我们会在 N 这个维度上将权重矩阵拆分,优先拆分得到 Kx48 的子块(3.4 中说明优先选取 48 的原因),进行循环操作,不足 48 的部分拆分成 32、16、8、4、1等。
计算核函数解决了快速实现拆分后矩阵的乘法的问题。例如,上述矩阵拆分后,会生成 MxK 和 Kx48 两个矩阵的相乘问题,我们基于汇编语言实现了 FP32 和 INT8 数值精度下的核函数。
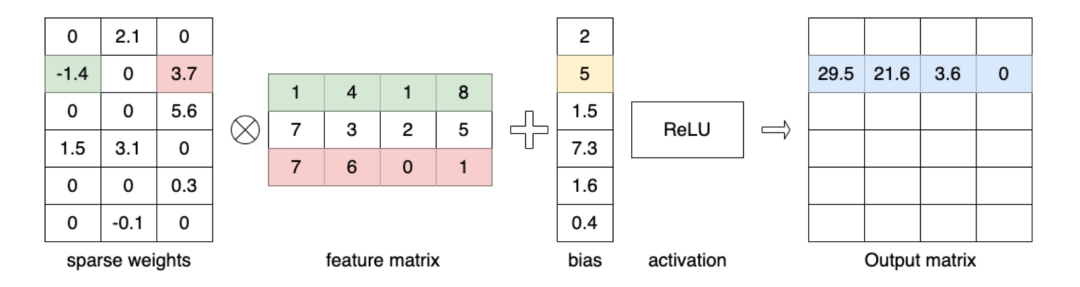
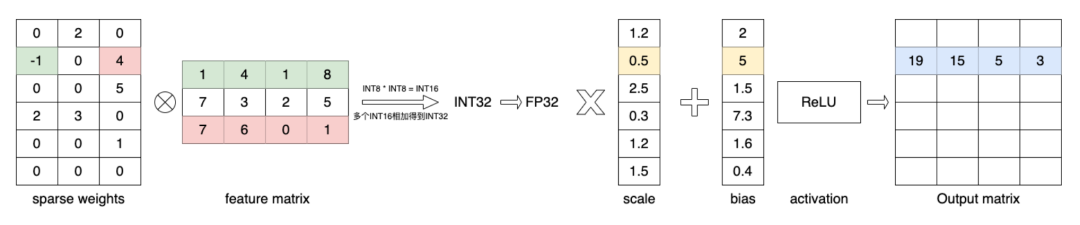
由于不涉及数值精度的转换,FP32 的 Kernel 计算逻辑相对直接,对于特征矩阵,如下图,我们在汇编语言下实现了与稀疏权重矩阵的乘法、与 Bias 的加法、以及激活函数操作。
而在汇编语言下,INT8 的计算核函数实现虽与 FP32 大体逻辑相似,但是很容易由于数值溢出带来一定的计算误差,所以如下图,我们需要额外注意
将 INT8 的数据转换为 INT16 和 INT32 的中间格式进行运算。
为了最大化寄存器使用率以及合理安排数据读取和处理的时间平衡,我们实践了如下策略。
-
汇编指令重排:
指令重排通过减少寄存器之间的依赖,达到并行执行指令的效果。例如,避免将当前指令的目的寄存器作为下一条指令的源寄存器,从而充分利用多级流水线,使指令并行执行。
-
数据预读取:
提前将下一次计算用到的数据从内存读取到缓存中,寄存器可以直接从缓存中加载数据,从而加快数据读取的速度。
-
对特征矩阵的 N 维度(即 HxW)进行分块操作:
主要是为了降低 Cache miss,同时考虑到 ARMv8/ARMv7 提供的向量寄存器数目,我们最大选取了48,然后依次为32、16、8、4、1,从而加速推理计算。
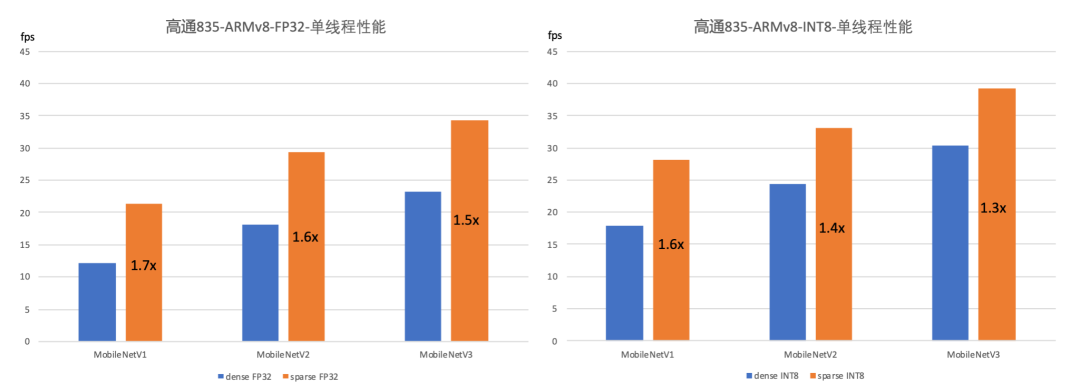
在精度损失在 1% 上下时,我们列举出 FP32 和 INT8 数值精度下 MobileNetV1, MobileNetV2 和 MobileNetV3 的加速情况如下:
-
对于FP32 的稀疏化 MobileNet 模型,较稠密 FP32 模型加速 50%~70%。
-
对于INT8 的稀疏化 MobileNet 模型,较稠密 FP32 模型加速 70%~130%;较稠密 INT8 模型加速 30%~60%。
综上,我们已经基本实现了从稀疏化模型训练到推理部署这样一个端到端的能力。但是实际应用中我们需要解决精度与速度的矛盾:如何快速选定一个合适的稀疏度,达到精度基本无损,且有符合预期的加速收益。解决措施是根据硬件延迟表,通过查询/预估的方式,选定符合加速要求的稀疏度下限。
此外,在应用面角度,稀疏矩阵乘法在全连接层和卷积核为 1 的卷积操作证明了收益,应用场景包括:
-
移动端和嵌入式端应用广泛(小模型的1x1卷积耗时占比较大)
-
同时,为了进一步扩大应用场景,提升稀疏模型加速效果,我们也在探索非结构化稀疏能为 3x3、5x5 卷积计算的带来的加速效果。
-
[1] Elsen, Erich, et al. "Fast sparse convnets." Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2020. paper, code
-
[2] Gou, Jianping, et al. "Knowledge distillation: A survey." International Journal of Computer Vision 129.6 (2021): 1789-1819.
-
[3] Neuralmagic. "An Intro to Gradual Magnitude Pruning (GMP)." https://neuralmagic.com/blog/pruning-gmp/ 2020, Aug 10.
-
[4] Lei, Deren, et al. "Implicit regularization of stochastic gradient descent in natural language processing: Observations and implications." arXiv preprint arXiv:1811.00659 (2018).
-
[5] Han, Song, et al. "Learning both weights and connections for efficient neural networks." arXiv preprint arXiv:1506.02626 (2015).