


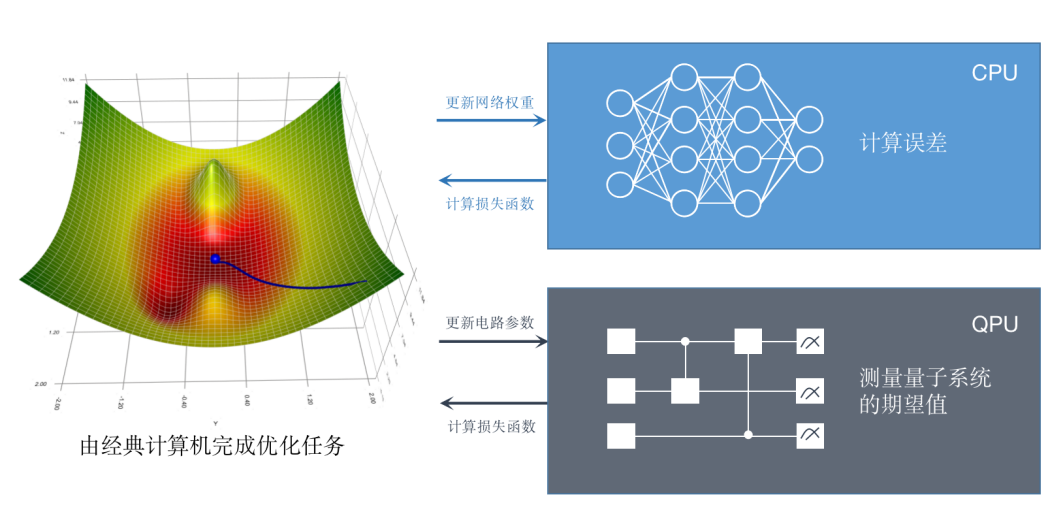
 图1 经典神经网络与量子神经网络对比图
图1 经典神经网络与量子神经网络对比图
量子神经网络的基础知识
示例: 如何通过量桨创建量子神经网络 QNN?
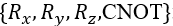 这四种量子门的模板,它们很容易在近期的超导量子设备上实现。以下图为例:
这四种量子门的模板,它们很容易在近期的超导量子设备上实现。以下图为例:
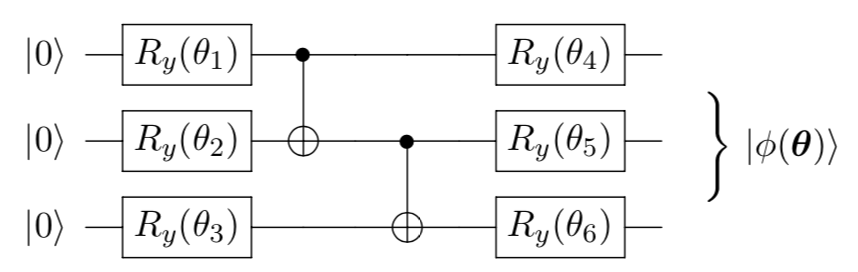 图2
图2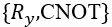 组成的简单量子神经网络,共计6个参数
组成的简单量子神经网络,共计6个参数
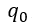 ,依次往下。从左到右代表我们施加门的时间顺序,先施加最左边的单比特参数化旋转门。接下来,我们来看看如何在量桨上建造这个简单的三比特量子神经网络:
,依次往下。从左到右代表我们施加门的时间顺序,先施加最左边的单比特参数化旋转门。接下来,我们来看看如何在量桨上建造这个简单的三比特量子神经网络:
# 引入必要的包
import numpy as np
import paddle
from paddle_quantum.circuit import UAnsatz
# 随机初始化参数
theta = np.random.rand(6)
# 我们需要将 Numpy array 转换成飞桨中的 Tensor
theta = paddle.to_tensor(theta)
# 初始化量子电路
num_qubits = 3
cir = UAnsatz(num_qubits)
# 添加单比特旋转门
cir.ry(theta[0], 0)
cir.ry(theta[1], 1)
cir.ry(theta[2], 2)
# 添加两比特门
cir.cnot([0, 1])
cir.cnot([1, 2])
# 添加单比特旋转门
cir.ry(theta[3], 0)
cir.ry(theta[4], 1)
cir.ry(theta[5], 2)
print('图中量子神经网络结构和参数为:')
print(cir) 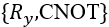 构成的组合电路,并可以通过有限个这样的电路的组合,来近似各种不同而复杂的门电路。这里有点像乐高积木,我们可以在积木堆里加入各种各样的小积木然后去拼出一个目标大积木。关于量子门的近似,总体上是一个困难的问题,感兴趣的读者可以参考AI Studio常规赛中的量子电路合成赛题:
构成的组合电路,并可以通过有限个这样的电路的组合,来近似各种不同而复杂的门电路。这里有点像乐高积木,我们可以在积木堆里加入各种各样的小积木然后去拼出一个目标大积木。关于量子门的近似,总体上是一个困难的问题,感兴趣的读者可以参考AI Studio常规赛中的量子电路合成赛题:
量子机器学习案例
用 VQE求解氢分子的基态能量
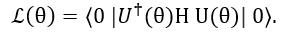
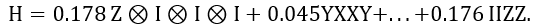
上述结构通常被称为泡利字符串(Pauli string)的形式,其中{X, Y, Z}是泡利矩阵,I表示单位矩阵,符号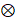
# 导入相关库
import numpy as np
import paddle
from paddle_quantum.circuit import UAnsatz
from paddle_quantum.utils import pauli_str_to_matrix
from paddle_quantum.VQE.chemistrysub import H2_generator
# 读取内置好的泡利字符串形式的氢分子哈密顿量
Hamiltonian, N = H2_generator() # N 表示量子比特个数,这里为4
# 超参数设置
ITR = 80 # 设置训练的总迭代次数
LR = 0.4 # 设置学习率
D = 2 # 设置量子神经网络中重复计算模块的深度 Depth
# 把记录的关于哈密顿量的转化为矩阵表示
H_matrix = pauli_str_to_matrix(Hamiltonian, N)
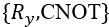 组成的模块化QNN。可以重复同一模块加深QNN的表达能力,这点和增加经典神经网络的深度是异曲同工的。注意这里我们直接调用了在量桨中内置好的网络模板 `real_entangled_layer`。读者可以在量桨API中找到更为详细的说明。
组成的模块化QNN。可以重复同一模块加深QNN的表达能力,这点和增加经典神经网络的深度是异曲同工的。注意这里我们直接调用了在量桨中内置好的网络模板 `real_entangled_layer`。读者可以在量桨API中找到更为详细的说明。
# 构造量子神经网路
def U_theta(theta, Hamiltonian, N, D):
"""
Quantum Neural Network
"""
# 按照量子比特数量/网络宽度初始化量子神经网络
cir = UAnsatz(N)
# 内置的 {R_y + CNOT} 电路模板
cir.real_entangled_layer(theta[:D], D)
# 量子神经网络作用在默认的初始态 |0000>上
cir.run_state_vector()
# 计算给定哈密顿量的期望值,也就是损失函数
loss = cir.expecval(Hamiltonian)
return loss, cir
class vqeNet(paddle.nn.Layer):
def __init__(self, shape, dtype="float64"):
super(vqeNet, self).__init__()
# 初始化 theta 参数列表,并用 [0, 2*pi] 的均匀分布来填充初始值
self.theta = self.create_parameter(shape=shape,
default_initializer=paddle.nn.initializer.Uniform(low=0.0, high=2*np.pi),
dtype=dtype, is_bias=False)
# 定义损失函数和前向传播机制
def forward(self, N, D):
# 计算损失函数/期望值
loss, cir = U_theta(self.theta, Hamiltonian, N, D)
return loss, cir
# 确定网络的参数维度
net = vqeNet(shape=[D, N, 1])
# 我们利用Adam优化器来获得相对好的收敛
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=net.parameters())
# 优化循环
for itr in range(1, ITR + 1):
# 前向传播计算损失函数
loss, cir = net(N, D)
# 在动态图机制下,反向传播极小化损失函数
loss.backward()
opt.minimize(loss)
opt.clear_grad()
# 打印结果
if itr % 20 == 0:
print("循环:", itr, "VQE估计出的基态能量:", "%.4f Ha"
% loss.numpy())
if itr == ITR:
print("和真实基态能量的误差为:", 100*np.abs(loss.numpy()+1.136189454065923)/(1.136189454065923), "%")
print("\n训练后的QNN:")
print(cir)
>
循环:20 VQE估计出的基态能量:-1.0521 Ha
循环:40 VQE估计出的基态能量:-1.1233 Ha
循环:60 VQE估计出的基态能量:-1.1358 Ha
循环:80 VQE估计出的基态能量:-1.1361 Ha
和真实基态能量的误差为:0.00850696%
--Ry(4.709)----*--------------X----Ry(1.573)----*--------------X--
| | | |
--Ry(4.712)----X----*---------|----Ry(1.366)----X----*---------|--
| | | |
--Ry(1.560)---------X----*----|----Ry(1.576)---------X----*----|--
| | | |
--Ry(1.561)--------------X----*----Ry(-1.58)--------------X----*--
结束语
参考文献

飞桨(PaddlePaddle)以百度多年的深度学习技术研究和业务应用为基础,集深度学习核心训练和推理框架、基础模型库、端到端开发套件和丰富的工具组件于一体,是中国首个自主研发、功能丰富、开源开放的产业级深度学习平台。飞桨企业版针对企业级需求增强了相应特性,包含零门槛AI开发平台EasyDL和全功能AI开发平台BML。EasyDL主要面向中小企业,提供零门槛、预置丰富网络和模型、便捷高效的开发平台;BML是为大型企业提供的功能全面、可灵活定制和被深度集成的开发平台。
END


 图1 经典神经网络与量子神经网络对比图
图1 经典神经网络与量子神经网络对比图
量子神经网络的基础知识
示例: 如何通过量桨创建量子神经网络 QNN?
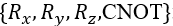 这四种量子门的模板,它们很容易在近期的超导量子设备上实现。以下图为例:
这四种量子门的模板,它们很容易在近期的超导量子设备上实现。以下图为例:
 图2
图2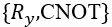 组成的简单量子神经网络,共计6个参数
组成的简单量子神经网络,共计6个参数
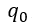 ,依次往下。从左到右代表我们施加门的时间顺序,先施加最左边的单比特参数化旋转门。接下来,我们来看看如何在量桨上建造这个简单的三比特量子神经网络:
,依次往下。从左到右代表我们施加门的时间顺序,先施加最左边的单比特参数化旋转门。接下来,我们来看看如何在量桨上建造这个简单的三比特量子神经网络:
# 引入必要的包
import numpy as np
import paddle
from paddle_quantum.circuit import UAnsatz
# 随机初始化参数
theta = np.random.rand(6)
# 我们需要将 Numpy array 转换成飞桨中的 Tensor
theta = paddle.to_tensor(theta)
# 初始化量子电路
num_qubits = 3
cir = UAnsatz(num_qubits)
# 添加单比特旋转门
cir.ry(theta[0], 0)
cir.ry(theta[1], 1)
cir.ry(theta[2], 2)
# 添加两比特门
cir.cnot([0, 1])
cir.cnot([1, 2])
# 添加单比特旋转门
cir.ry(theta[3], 0)
cir.ry(theta[4], 1)
cir.ry(theta[5], 2)
print('图中量子神经网络结构和参数为:')
print(cir) 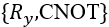 构成的组合电路,并可以通过有限个这样的电路的组合,来近似各种不同而复杂的门电路。这里有点像乐高积木,我们可以在积木堆里加入各种各样的小积木然后去拼出一个目标大积木。关于量子门的近似,总体上是一个困难的问题,感兴趣的读者可以参考AI Studio常规赛中的量子电路合成赛题:
构成的组合电路,并可以通过有限个这样的电路的组合,来近似各种不同而复杂的门电路。这里有点像乐高积木,我们可以在积木堆里加入各种各样的小积木然后去拼出一个目标大积木。关于量子门的近似,总体上是一个困难的问题,感兴趣的读者可以参考AI Studio常规赛中的量子电路合成赛题:
量子机器学习案例
用 VQE求解氢分子的基态能量
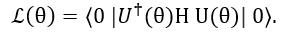
上述结构通常被称为泡利字符串(Pauli string)的形式,其中{X, Y, Z}是泡利矩阵,I表示单位矩阵,符号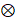
# 导入相关库
import numpy as np
import paddle
from paddle_quantum.circuit import UAnsatz
from paddle_quantum.utils import pauli_str_to_matrix
from paddle_quantum.VQE.chemistrysub import H2_generator
# 读取内置好的泡利字符串形式的氢分子哈密顿量
Hamiltonian, N = H2_generator() # N 表示量子比特个数,这里为4
# 超参数设置
ITR = 80 # 设置训练的总迭代次数
LR = 0.4 # 设置学习率
D = 2 # 设置量子神经网络中重复计算模块的深度 Depth
# 把记录的关于哈密顿量的转化为矩阵表示
H_matrix = pauli_str_to_matrix(Hamiltonian, N)
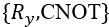 组成的模块化QNN。可以重复同一模块加深QNN的表达能力,这点和增加经典神经网络的深度是异曲同工的。注意这里我们直接调用了在量桨中内置好的网络模板 `real_entangled_layer`。读者可以在量桨API中找到更为详细的说明。
组成的模块化QNN。可以重复同一模块加深QNN的表达能力,这点和增加经典神经网络的深度是异曲同工的。注意这里我们直接调用了在量桨中内置好的网络模板 `real_entangled_layer`。读者可以在量桨API中找到更为详细的说明。
# 构造量子神经网路
def U_theta(theta, Hamiltonian, N, D):
"""
Quantum Neural Network
"""
# 按照量子比特数量/网络宽度初始化量子神经网络
cir = UAnsatz(N)
# 内置的 {R_y + CNOT} 电路模板
cir.real_entangled_layer(theta[:D], D)
# 量子神经网络作用在默认的初始态 |0000>上
cir.run_state_vector()
# 计算给定哈密顿量的期望值,也就是损失函数
loss = cir.expecval(Hamiltonian)
return loss, cir
class vqeNet(paddle.nn.Layer):
def __init__(self, shape, dtype="float64"):
super(vqeNet, self).__init__()
# 初始化 theta 参数列表,并用 [0, 2*pi] 的均匀分布来填充初始值
self.theta = self.create_parameter(shape=shape,
default_initializer=paddle.nn.initializer.Uniform(low=0.0, high=2*np.pi),
dtype=dtype, is_bias=False)
# 定义损失函数和前向传播机制
def forward(self, N, D):
# 计算损失函数/期望值
loss, cir = U_theta(self.theta, Hamiltonian, N, D)
return loss, cir
# 确定网络的参数维度
net = vqeNet(shape=[D, N, 1])
# 我们利用Adam优化器来获得相对好的收敛
opt = paddle.optimizer.Adam(learning_rate=LR, parameters=net.parameters())
# 优化循环
for itr in range(1, ITR + 1):
# 前向传播计算损失函数
loss, cir = net(N, D)
# 在动态图机制下,反向传播极小化损失函数
loss.backward()
opt.minimize(loss)
opt.clear_grad()
# 打印结果
if itr % 20 == 0:
print("循环:", itr, "VQE估计出的基态能量:", "%.4f Ha"
% loss.numpy())
if itr == ITR:
print("和真实基态能量的误差为:", 100*np.abs(loss.numpy()+1.136189454065923)/(1.136189454065923), "%")
print("\n训练后的QNN:")
print(cir)
>
循环:20 VQE估计出的基态能量:-1.0521 Ha
循环:40 VQE估计出的基态能量:-1.1233 Ha
循环:60 VQE估计出的基态能量:-1.1358 Ha
循环:80 VQE估计出的基态能量:-1.1361 Ha
和真实基态能量的误差为:0.00850696%
--Ry(4.709)----*--------------X----Ry(1.573)----*--------------X--
| | | |
--Ry(4.712)----X----*---------|----Ry(1.366)----X----*---------|--
| | | |
--Ry(1.560)---------X----*----|----Ry(1.576)---------X----*----|--
| | | |
--Ry(1.561)--------------X----*----Ry(-1.58)--------------X----*--
结束语
参考文献

飞桨(PaddlePaddle)以百度多年的深度学习技术研究和业务应用为基础,集深度学习核心训练和推理框架、基础模型库、端到端开发套件和丰富的工具组件于一体,是中国首个自主研发、功能丰富、开源开放的产业级深度学习平台。飞桨企业版针对企业级需求增强了相应特性,包含零门槛AI开发平台EasyDL和全功能AI开发平台BML。EasyDL主要面向中小企业,提供零门槛、预置丰富网络和模型、便捷高效的开发平台;BML是为大型企业提供的功能全面、可灵活定制和被深度集成的开发平台。
END
