

真空环境中,火箭发动机喷流向外部环境自由膨胀形成羽毛状流场,称为真空羽流[1]。真空羽流对航天器产气动力、气动热、污染、电磁干扰和视场干扰等效应统称为羽流效应。羽流效应会干扰航天器正常工作状态,甚至影响航天器寿命和任务成败。因此,真空羽流及其效应评估和防护是航天领域的重要科学和工程问题。

本文作者:张百一,北京航空航天大学博士研究生、飞桨开发者技术专家(PPDE)
图1 嫦娥五号落月过程影像
本文针对月面探测器月面着陆过程,分别通过CNN-DSMC和DSMC方法实现月面探测器在不同悬停高度时的真空羽流流场计算。
问题描述
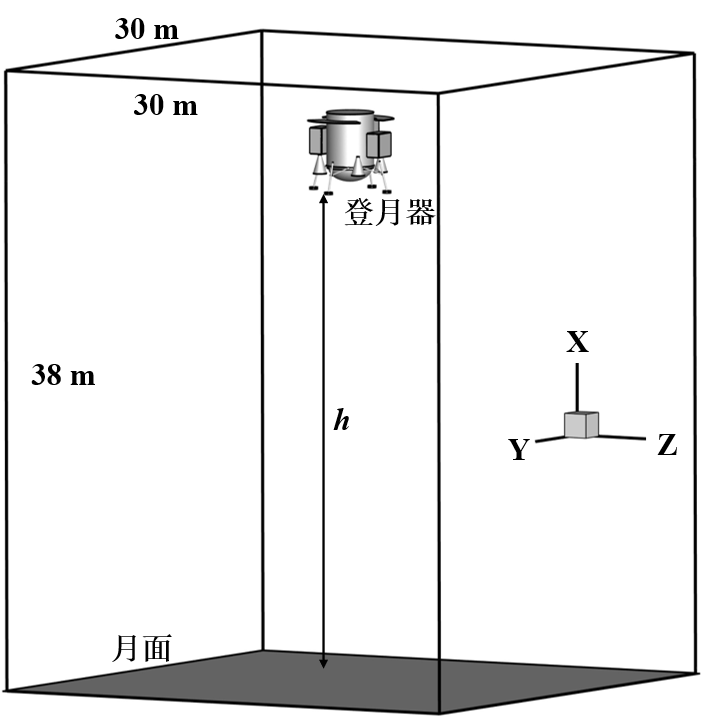
图3 月面着陆过程羽流仿真计算域示意图
计算流程
在CNN-DSMC方法中,计算分为数据预处理和模型训练两个过程。在数据预处理中,真空羽流仿真模型中的几何拓扑信息被抽象为符号距离函数(Signed Distance Function, SDF),边界条件信息被抽象为标识符矩阵(Identifier Matrix, IM)。SDF和IM共同作为训练集的输入,由DSMC数值模拟得到的真空羽流速度场(三个方向)和密度场作为训练集的输出,测试集为未参与训练的DSMC数值模拟算例,用于验证CNN-DSMC方法的准确性。在完成训练之后,就得到了真空羽流智能计算模型。
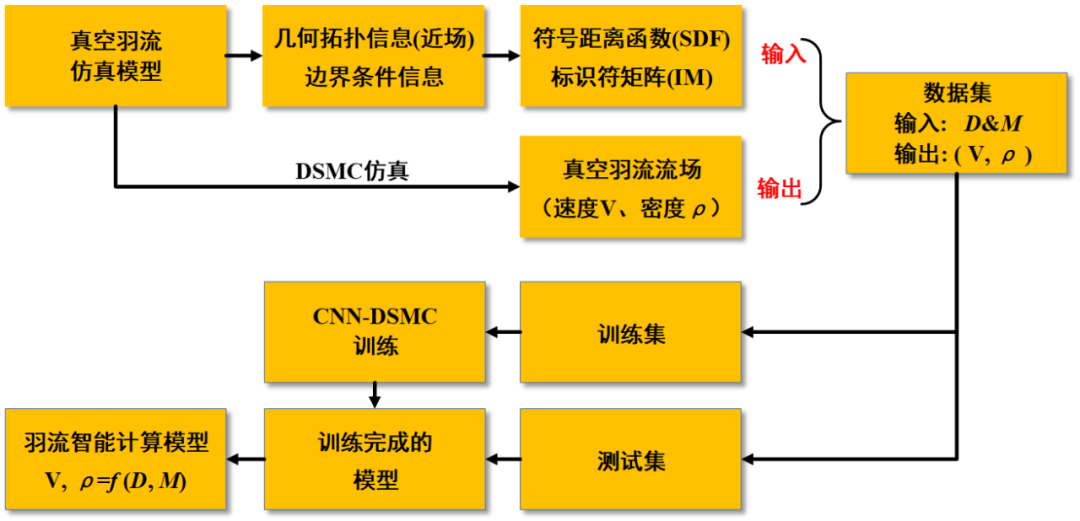
图4 CNN-DSMC方法的计算总体流程
下面是基于飞桨构建的训练函数:
def epoch(loader, training=False):
total_loss = 0
if training:
model.train()
else:
model.eval()
使用GPU
with paddle.static.device_guard('gpu'):
遍历数据集
for tensors in loader:
loss, output = loss_func(model, tensors)
if training:
optimizer.clear_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
return total_loss
训练主循环
def train():
for epoch_id in range(1, epochs + 1):
begin = time.time()
print("Epoch #" + str(epoch_id))
训练过程
train_loss = epoch(train_loader, training=True)
print("\tTrain Loss = " + str(train_loss))
测试过程
with paddle.no_grad():
val_loss = epoch(test_loader, training=False)
print("\tValidation Loss = " + str(val_loss))
输出一个epoch的时间
if (epoch_id != 0):
print("运行1个epochs的时间为{:.2f} s".format(time.time() - begin))
if (epoch_id % 2 == 0):
paddle.save(model.state_dict(), os.path.join(save_path, "CNN-DSMC" + str(epoch_id) + ".pdparams"))
print("Model saved!")下面是使用飞桨框架训练的主代码。其中,优化器采用了飞桨提供的AdamW优化器,这个优化器具有权重衰减功能,相比Adam可以有效地提高模型的泛化性能:
import os
import pickle
from utils import *
from paddle.io import TensorDataset, DataLoader
from net import CNN_DSMC
import time
创建保存路径
save_path = r"./Run"
if not os.path.exists(save_path):
os.makedirs(save_path)加载原始数据
x = pickle.load(open("./data/dataX.pkl", "rb"))
y = pickle.load(open("./data/dataY.pkl", "rb"))
x = paddle.to_tensor(x, dtype="float32")
y = paddle.to_tensor(y, dtype="float32")
分割数据集
train_data, test_data = split_tensors(x, y, ratio=10 / 12)
train_dataset, test_dataset = TensorDataset([train_data[0], train_data[1]]), TensorDataset(
[test_data[0], test_data[1]])超参数设置
lr = 0.001
epochs = 20000
batch_size = 2
kernel_size = 5
filters = [8, 16, 32, 32, 64, 64, 128]
model = CNN_DSMC(2, 4, filters=filters, kernel_size=kernel_size)
wd = 0.005优化器设置
optimizer = paddle.optimizer.AdamW(learning_rate=lr, parameters=model.parameters(), weight_decay=wd)加载数据集
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
开始训练
train()模型介绍
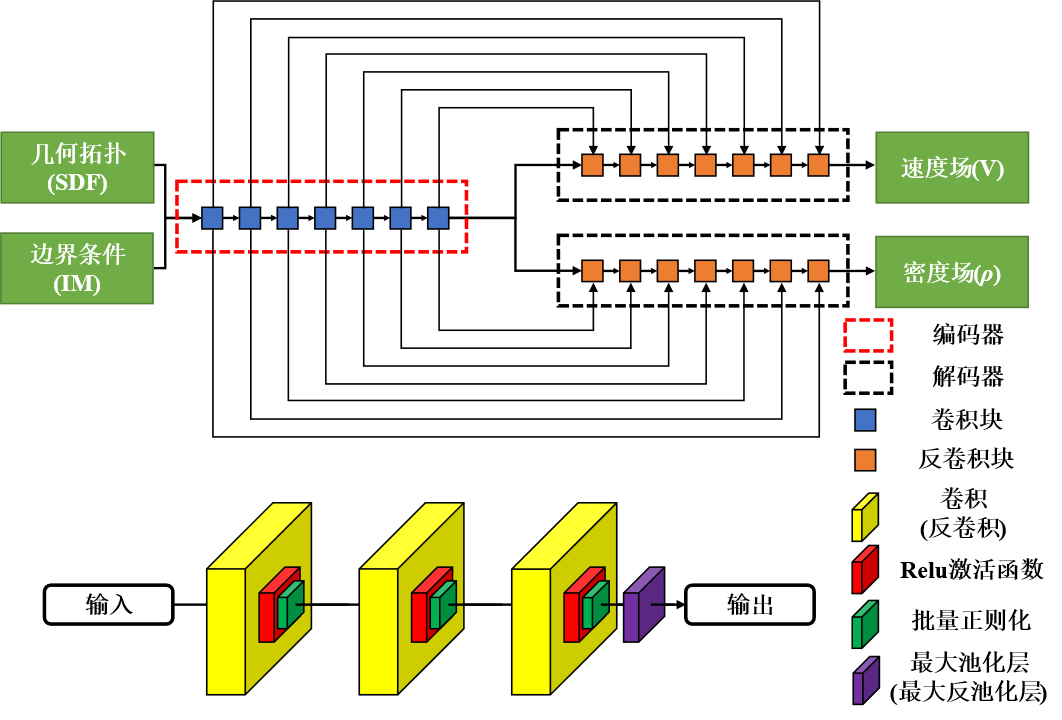
图5 CNN-DSMC使用的卷积神经网络结构
使用飞桨进行模型构建代码如下,其中,特别使用到了飞桨中的Conv3D、 Conv3DTranspose、max_pool3d和max_unpool3d用来构成模型中的Autoencoder结构:
class CNN_DSMC(nn.Layer):
def __init__(self, in_channels, out_channels, kernel_size=3, filters=[16, 32, 64], layers=3, weight_norm=False, batch_norm=True, activation=nn.ReLU, final_activation=None):
super().__init__()
assert len(filters) > 0
self.final_activation = final_activation
self.encoder = create_encoder(in_channels, filters, kernel_size, weight_norm, batch_norm, activation, layers)
decoders = []
for i in range(out_channels):
decoders.append(create_decoder(1, filters, kernel_size, weight_norm, batch_norm, activation, layers))
self.decoders = nn.Sequential(*decoders)定义编码器
def encode(self, x):
tensors = []
indices = []
sizes = []
for encoder in self.encoder:
x = encoder(x)
sizes.append(x.shape)
tensors.append(x)
x, ind = F.max_pool3d(x, 2, 2, return_mask=True)
indices.append(ind)
return x, tensors, indices, sizes
定义解码器
def decode(self, _x, _tensors, _indices, _sizes):
y = []
for _decoder in self.decoders:
x = _x
tensors = _tensors[:]
indices = _indices[:]
sizes = _sizes[:]
for decoder in _decoder:
tensor = tensors.pop()
size = sizes.pop()
ind = indices.pop()
x = F.max_unpool3d(x, ind, 2, 2, output_size=size)
x = paddle.concat([tensor, x], axis=1)
x = decoder(x)
y.append(x)
return paddle.concat(y, axis=1)
def forward(self, x):
x, tensors, indices, sizes = self.encode(x)
x = self.decode(x, tensors, indices, sizes)
if self.final_activation is not None:
x = self.final_activation(x)
return x数据处理
在CNN-DSMC方法中,真空羽流仿真模型中的几何拓扑信息被抽象为SDF,定义Ω为度量空间X的一个子空间,SDF定义如下:
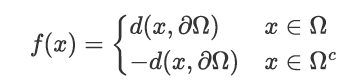
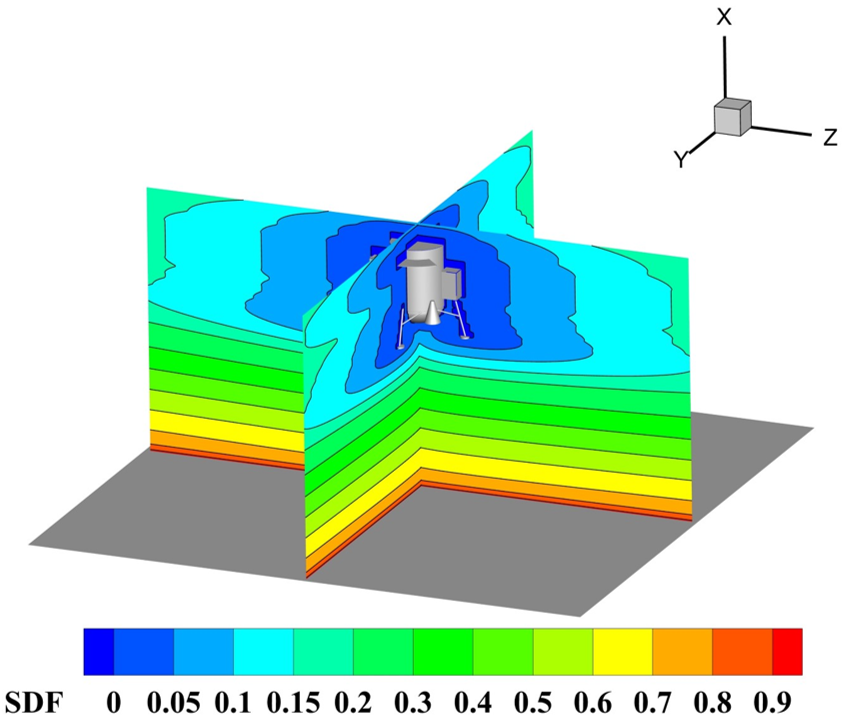
图6 代表几何拓扑信息的符号距离函数(SDF)
在CNN-DSMC中,边界条件信息被抽象为IM。IM本质上是一个三维的矩阵,其矩阵元素作为区分三维空间不同区域的标识符。在本文中,共选取4种不同的标识符:开放边界、航天器边界、月面边界和真空羽流区域,这4种标识符也与实际DSMC数值模拟中使用的边界条件相对应。具体设置如下图所示。
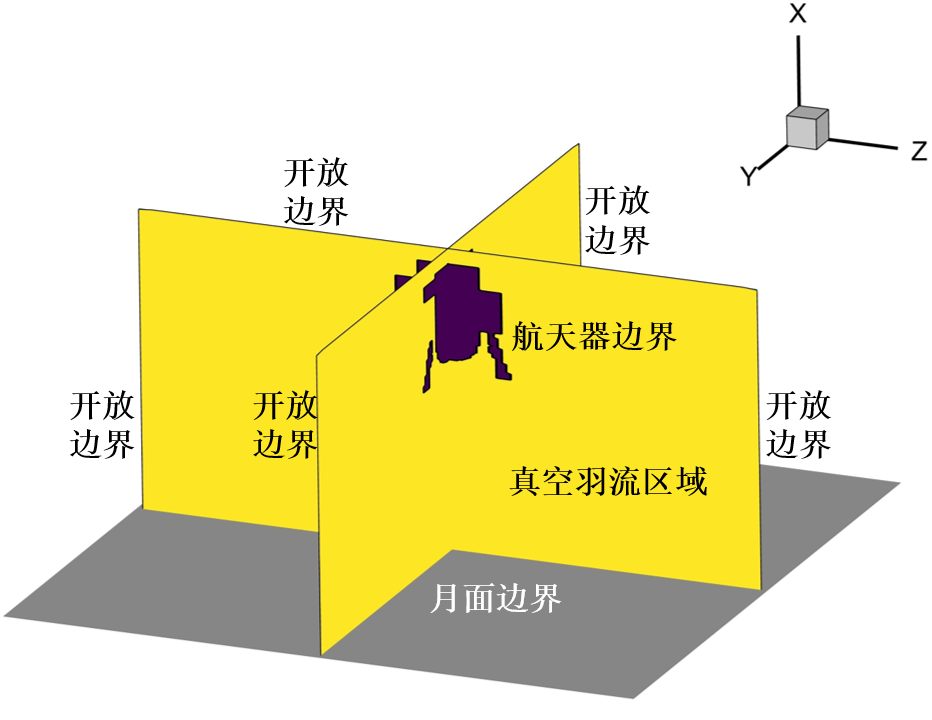
图7 代表边界条件信息的标识符矩阵(IM)
将DSMC计算得到的数据输入CNN-DSMC网络中进行训练,共训练40000步,利用如下代码进行测试:
模型路径
path = r"./Run/CNN-DSMC.pdparams"初步设置网络
kernel_size = 5
filters = [8, 16, 32, 32, 64, 64, 128]
net = CNN_DSMC(2, 4, filters=filters, kernel_size=kernel_size)加载模型参数
net.set_state_dict(paddle.load(path))加载数据
x = pickle.load(open("./data/dataX.pkl", "rb"))
y = pickle.load(open("./data/dataY.pkl", "rb"))
x = paddle.to_tensor(x, dtype="float32")
y = paddle.to_tensor(y, dtype="float32")
train_data, test_data = split_tensors(x, y, ratio=10 / 12)
train_dataset, test_dataset = TensorDataset([train_data[0], train_data[1]]), TensorDataset(
[test_data[0], test_data[1]])
test_x, test_y = test_dataset[:]
模型运行
out = net(test_x)读取流场坐标
coord = pickle.load(open("./coord.pkl", "rb"))
XX = np.unique(coord["x"])
YY = np.unique(coord["y"])
ZZ = np.unique(coord["z"])
导出流场预测数据,并转换为国际制单位
s = 0
rho = 10 ** (-10 * out[s, 3, :, :, :]) - 1e-10
u = out[s, 0, :, :, :] * (-5010)
v = out[s, 1, :, :, :] * (-5010)
w = out[s, 2, :, :, :] * (-5010)
ux_pre = u.detach().numpy()
uy_pre = v.detach().numpy()
uz_pre = w.detach().numpy()
rho_pre = rho.detach().numpy()
ux_pre = np.flip(ux_pre)
uy_pre = np.flip(uy_pre)
uz_pre = np.flip(uz_pre)
rho_pre = np.flip(rho_pre)
with open("result_pre.dat", 'w') as f:
f.writelines("variables=\"X\",\"Y\",\"Z\",\"ux\",\"uy\",\"uz\",\"rho\"\n")
f.writelines("zone i=300 j=100 k=100\n")
for idz, Z in enumerate(ZZ):
for idy, Y in enumerate(YY):
for idx, X in enumerate(XX):
f.writelines( "{:.6e}\t{:.6e}\t{:.6e}\t{:.6e}\t{:.6e}\t{:.6e}\t{:.6e}\n".format(X, Y, Z, ux_pre[idx, idy, idz], uy_pre[idx, idy, idz], uz_pre[idx, idy, idz], rho_pre[idx, idy, idz]))
首先得到了h=8.2m情况下的真空羽流速度场的DSMC数值模拟结果和CNN-DSMC计算结果,如下图所示。可以看出,两者得到的速度场几乎完全一致,CNN-DSMC计算的激波形状也与DSMC数值模拟结果一致。图中也给出了流线的分布,结果表明DSMC数值模拟结果和CNN-DSMC计算的粒子运动轨迹也基本相同。
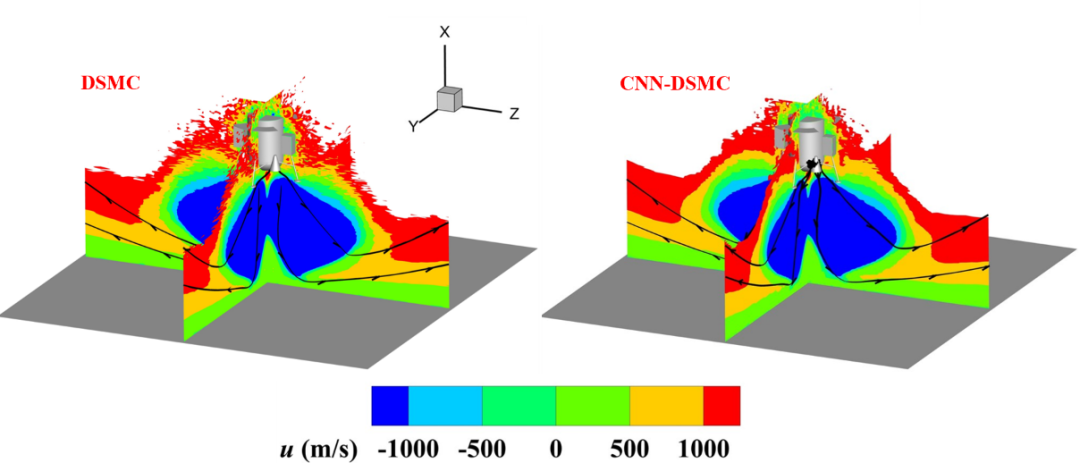
图8 真空羽流速度场的DSMC数值模拟结果(左)
下图分别给出了月球探测器轴线处速度和密度的变化曲线,范围为-9m到-1 m,其中,-9m对应于月面位置,-1m对应于月球探测器正下方与足垫同一高度的位置。结果表明,CNN-DSMC计算得到的速度和密度与DSMC数值模拟结果基本一致,其平均相对误差分别为6.0%和8.8%。
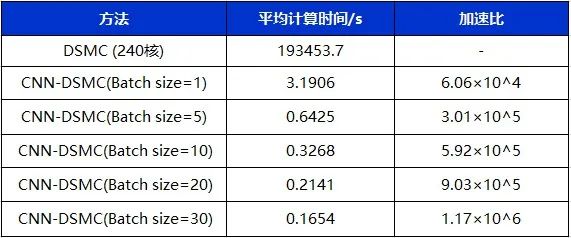
表1 CNN-DSMC和DSMC方法计算时间对比
模型训练
python
git clone https://github.com/X4Science/CNN_DSMC.git # clone the repo
cd CNN_DSMC
chmod 777 main.py
python main.py # 开始训练,训练前请先下载数据模型推理
python
python ./database.py # 先在文件中设置好模型路径参考文献
[1] HE B, ZHANG J, CAI G. Research on vacuum plume and its effects[J]. Chinese Journal of Aeronautics, 2013, 26(1): 27-36.
[2] HE B, HE X, ZHANG M, et al. Plume aerodynamic effects of cushion engine in lunar landing[J]. Chinese Journal of Aeronautics, 2013, 26(2): 269-278.
拓展阅读
相关地址
AI Studio链接
https://aistudio.baidu.com/aistudio/projectdetail/4486133
Github repo
https://github.com/X4Science/CNN_DSMC/tree/main/CNN_DSMC
论文链接

关注【飞桨PaddlePaddle】公众号
获取更多技术内容~